人教版初中数学2023-2024学年八年级下学期课时基础练习 18.2特殊的平行四边形
试卷更新日期:2024-04-08 类型:同步测试
一、选择题
-
1. 如图,在矩形 中, 、 分别是边 、 上的点, ,连接 、 , 与对角线 交于点 ,且 , , ,则 的长为( )
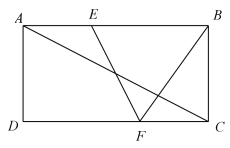 A、 B、 C、4 D、62. 如图,在面积为S的菱形ABCD中,对角线AC,BD相交于点O,E,F,G分别是BC,OB,OC的中点,则四边形EFOG的面积为( )
A、 B、 C、4 D、62. 如图,在面积为S的菱形ABCD中,对角线AC,BD相交于点O,E,F,G分别是BC,OB,OC的中点,则四边形EFOG的面积为( )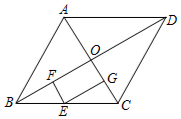 A、 B、 C、 D、3. 如图,为正方形对角线的中点,为等边三角形.若 , 则的长度为( )
A、 B、 C、 D、3. 如图,为正方形对角线的中点,为等边三角形.若 , 则的长度为( ) A、 B、 C、 D、4. 如图,在中,为AB的中点,为AC的中点,是DE上一点,且 , 若 , 则线段EF的长为( )
A、 B、 C、 D、4. 如图,在中,为AB的中点,为AC的中点,是DE上一点,且 , 若 , 则线段EF的长为( ) A、2 B、3 C、4 D、55. 如图,在△ABC中,AB=AC=16,BC=12,AF⊥BC于点F , BE⊥AC于点E , D为AB的中点,M为EF的中点,则DM的长为( )
A、2 B、3 C、4 D、55. 如图,在△ABC中,AB=AC=16,BC=12,AF⊥BC于点F , BE⊥AC于点E , D为AB的中点,M为EF的中点,则DM的长为( )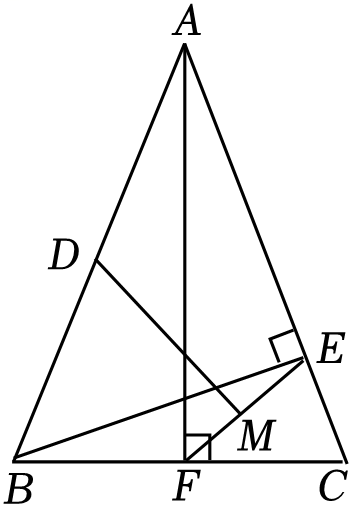 A、7 B、8 C、 D、6. 下列命题是假命题的是( )A、有一组邻边相等的矩形是正方形 B、对角线互相平分的四边形是平行四边形 C、有三个角是直角的四边形是矩形 D、有一组邻边相等的四边形是菱形7. 如图,矩形ABCD中,对角线AC、BD相交于点O , 过点O作OE⊥BD交AD于点E , 已知AB=5,△DOE的面积为 , 则DE的长为( )
A、7 B、8 C、 D、6. 下列命题是假命题的是( )A、有一组邻边相等的矩形是正方形 B、对角线互相平分的四边形是平行四边形 C、有三个角是直角的四边形是矩形 D、有一组邻边相等的四边形是菱形7. 如图,矩形ABCD中,对角线AC、BD相交于点O , 过点O作OE⊥BD交AD于点E , 已知AB=5,△DOE的面积为 , 则DE的长为( ) A、5 B、6 C、7 D、8. 如图,在矩形ABCD中,O为AC的中点,过点O作AC的垂线,分别交DC于点F,交AB于点E,G是AE的中点,且∠AOG=30°,有下列结论:①DC=3OG;②OG=BC;③连结AF,CE,四边形AECF为菱形;④其中正确的是( )
A、5 B、6 C、7 D、8. 如图,在矩形ABCD中,O为AC的中点,过点O作AC的垂线,分别交DC于点F,交AB于点E,G是AE的中点,且∠AOG=30°,有下列结论:①DC=3OG;②OG=BC;③连结AF,CE,四边形AECF为菱形;④其中正确的是( ) A、②③ B、③④ C、①②④ D、①③④9. 如图,菱形 ABCD的边长为 13,对角线AC=24,E,F分别是边 CD,BC 的中点,连结EF 并延长,与AB的延长线相交于点G,则 EG 的长为( )
A、②③ B、③④ C、①②④ D、①③④9. 如图,菱形 ABCD的边长为 13,对角线AC=24,E,F分别是边 CD,BC 的中点,连结EF 并延长,与AB的延长线相交于点G,则 EG 的长为( ) A、13 B、10 C、12 D、510. 如图▱ABCD的对角线AC,BD相交于点O,E为BC的中点,连结EO并延长,交AD于点F,∠ABC=60°,BC=2AB.给出下列结论:①AB⊥AC.②AD=4OE.③四边形AECF是菱形④其中正确的是( )
A、13 B、10 C、12 D、510. 如图▱ABCD的对角线AC,BD相交于点O,E为BC的中点,连结EO并延长,交AD于点F,∠ABC=60°,BC=2AB.给出下列结论:①AB⊥AC.②AD=4OE.③四边形AECF是菱形④其中正确的是( ) A、①②③④ B、①② C、①③ D、②③④
A、①②③④ B、①② C、①③ D、②③④二、填空题
-
11. 如图,矩形ABCD的对角线AC、BD相交于点O,过点O作OE⊥BC,垂足为点E,过点A作AF⊥OB,垂足为点F,若BC=2AF,OD=6,则BE的长为 .
 12. 如图,点E , F , G , H分别是四边形的边 , , , 的中点,连接四边形各边中点,当四边形满足条件,四边形是矩形.
12. 如图,点E , F , G , H分别是四边形的边 , , , 的中点,连接四边形各边中点,当四边形满足条件,四边形是矩形.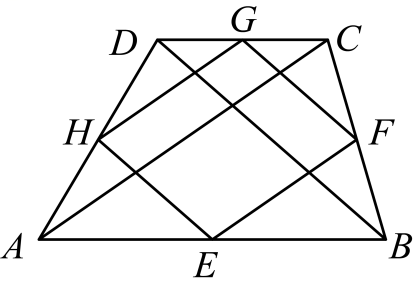 13. 如图, 中, , , ,D是AB的中点,E是BC的中点, 于点F,则 的长是.
13. 如图, 中, , , ,D是AB的中点,E是BC的中点, 于点F,则 的长是. 14. 如图,在菱形ABCD中,AB=10cm,AC=16cm,E,F分别是CD和BC的中点,连结EP并延长与AB的延长线相交于点G,则EG的长度为cm
14. 如图,在菱形ABCD中,AB=10cm,AC=16cm,E,F分别是CD和BC的中点,连结EP并延长与AB的延长线相交于点G,则EG的长度为cm 15. 如图,四边形是边长为4的正方形,是等边三角形,则阴影部分的面积为 .
15. 如图,四边形是边长为4的正方形,是等边三角形,则阴影部分的面积为 .
三、解答题
-
16. 如图①,已知AD//BC,AB//DC,∠B.
 (1)、求证:四边形ABCD为矩形;(2)、如图②,M为AD的中点,为AB的中点,.若 , 求BC的长.17. 如图,在正方形中,点是对角线上一动点,连接 , 作交于点 , 以和为邻边作矩形 .
(1)、求证:四边形ABCD为矩形;(2)、如图②,M为AD的中点,为AB的中点,.若 , 求BC的长.17. 如图,在正方形中,点是对角线上一动点,连接 , 作交于点 , 以和为邻边作矩形 . (1)、猜想: , 的位置关系是;(2)、求证: .18. 如图,已知在平行四边形ABCD中,AE平分∠BAD交BC于点E , 点F在AD上,AF=AB , 连接BF交AE于点O , 连接EF .
(1)、猜想: , 的位置关系是;(2)、求证: .18. 如图,已知在平行四边形ABCD中,AE平分∠BAD交BC于点E , 点F在AD上,AF=AB , 连接BF交AE于点O , 连接EF . (1)、求证:四边形ABEF是菱形;(2)、若BF=8,AB=5,求AE的长.
(1)、求证:四边形ABEF是菱形;(2)、若BF=8,AB=5,求AE的长.

