人教版初中数学2023-2024学年八年级下学期课时培优练习 18.1平行四边形
试卷更新日期:2024-04-08 类型:同步测试
一、选择题
-
1. 如图,四边形ABCD中,为BC延长线上一点,连接AE,AE交CD于点的平分线交AE于点G.若为CD的中点,6,则AC的值为( )
 A、9 B、 C、10 D、2. 如图,在平行四边形中,延长到 , 使 , 连接交于点 , 交于点 . 下列结论①;②;③;④;⑤ , 其中正确的有( )个.
A、9 B、 C、10 D、2. 如图,在平行四边形中,延长到 , 使 , 连接交于点 , 交于点 . 下列结论①;②;③;④;⑤ , 其中正确的有( )个. A、1 B、2 C、3 D、43. 如图,把 剪成三部分,边 , , 放在同一直线 上,点 都落在直线 上,直线 .在 中,若 ,则 的度数为( )
A、1 B、2 C、3 D、43. 如图,把 剪成三部分,边 , , 放在同一直线 上,点 都落在直线 上,直线 .在 中,若 ,则 的度数为( )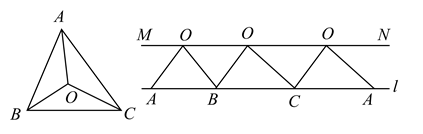 A、 B、 C、 D、4. 如图,BD为▱ABCD的对角线,∠DBC=45°,DE⊥BC于点E,BF⊥CD于点F,DE,BF相交于点H,直线BF交线段AD的延长线于点G,有下列结论:
A、 B、 C、 D、4. 如图,BD为▱ABCD的对角线,∠DBC=45°,DE⊥BC于点E,BF⊥CD于点F,DE,BF相交于点H,直线BF交线段AD的延长线于点G,有下列结论:①CE=BE;②∠A=∠BHE;③AB=BH;④∠BHD=∠BDG;⑤BH²+BG²=AG².其中正确的是( )
 A、①②④ B、②③⑤ C、①⑤ D、③④5. 如图,在平面直角坐标系中,▱OABC的顶点A,C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为( )
A、①②④ B、②③⑤ C、①⑤ D、③④5. 如图,在平面直角坐标系中,▱OABC的顶点A,C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为( ) A、3 B、4 C、5 D、66. 如图,在▱ABCD中,O是对角线AC上一点,连结 BO,DO.若△COD,△AOD,△AOB,△BOC 的面积分别为 S1 , S2 , S3 , S4 , 则下列关于 S1 , S2 , S3 , S4的等量关系中,不一定正确的是( )
A、3 B、4 C、5 D、66. 如图,在▱ABCD中,O是对角线AC上一点,连结 BO,DO.若△COD,△AOD,△AOB,△BOC 的面积分别为 S1 , S2 , S3 , S4 , 则下列关于 S1 , S2 , S3 , S4的等量关系中,不一定正确的是( ) A、 B、 C、 D、7. 如图,△ABC的面积为 24,点D为边AC 上的一点,连结BD 并延长,交 BC 的平行线AG 于点E,连结EC,以DE,EC为邻边作□DECF,DF 交边BC 于点 H,连结 AH.当 时,△AHC 的面积为 ( )
A、 B、 C、 D、7. 如图,△ABC的面积为 24,点D为边AC 上的一点,连结BD 并延长,交 BC 的平行线AG 于点E,连结EC,以DE,EC为邻边作□DECF,DF 交边BC 于点 H,连结 AH.当 时,△AHC 的面积为 ( )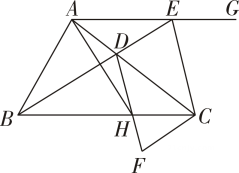 A、4 B、6 C、8 D、128. 如图,已知▱ABCD,点 E,F 在对角线AC 上,且AE=CF,连结 DE,DF,BE,BF.求证:四边形DEBF 为平行四边形.以下是排乱的证明过程:
A、4 B、6 C、8 D、128. 如图,已知▱ABCD,点 E,F 在对角线AC 上,且AE=CF,连结 DE,DF,BE,BF.求证:四边形DEBF 为平行四边形.以下是排乱的证明过程: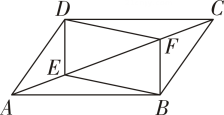
①∴四边形DEBF 为平行四边形.
②∵四边形ABCD为平行四边形,∴OD=OB,OA=OC.
③连结 BD,交 AC 于点O.
④∵AE=CF,∴OA-AE=OC-CF,即OE=OF.
证明步骤正确的顺序是 ( )
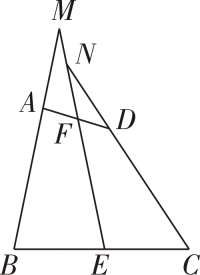
A、①②③④ B、③④②① C、③②④① D、④③②①9. 如图,M 是△ABC的边 BC 的中点,AN平分∠BAC,BN⊥AN,且 AB=10,MN=3,则AC的长( )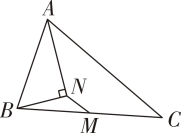 A、12 B、14 C、16 D、1810. 如图,在△ABC中,∠C=90°,E是CA延长线上-点,F是CB上一点,AE=12,BF=8,点P,Q,D分别是AF ,BE,AB的中点,则PQ的长为( )
A、12 B、14 C、16 D、1810. 如图,在△ABC中,∠C=90°,E是CA延长线上-点,F是CB上一点,AE=12,BF=8,点P,Q,D分别是AF ,BE,AB的中点,则PQ的长为( )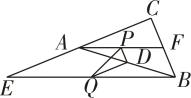 A、 B、4 C、6 D、
A、 B、4 C、6 D、二、填空题
-
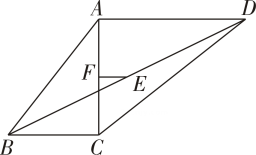
11. 如图,在平行四边形ABCD中, , , 以点C为圆心,以任意长为半径作弧,分别交CB , CD于点E , F , 再分别以E , F为圆心,以大于的长为半径作弧,两弧在内交于点P , 连接CP并延长交AD于点Q , 连接BQ . 若时,则与的周长之差为 .
 12. 如图,在▱ABCD中,对角线 AC,BD 相交于点O,E为BC 的中点,F,G为边CD 上的点,且 FG 连结OF,EG.若▱ABCD的面积为 60,则图中阴影部分的面积是.
12. 如图,在▱ABCD中,对角线 AC,BD 相交于点O,E为BC 的中点,F,G为边CD 上的点,且 FG 连结OF,EG.若▱ABCD的面积为 60,则图中阴影部分的面积是.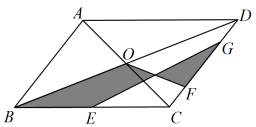 13. 如图,在四边形ABCD中,AB=2,CD=6,E,F,M分别为边BC,AD和对角线BD的中点连结EF,FM,则FM= , 线段EF的最大值为
13. 如图,在四边形ABCD中,AB=2,CD=6,E,F,M分别为边BC,AD和对角线BD的中点连结EF,FM,则FM= , 线段EF的最大值为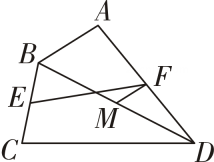 14. 如图,四边形中, , 且与不平行,P、M、N分别是、、的中点,则的范围是 .
14. 如图,四边形中, , 且与不平行,P、M、N分别是、、的中点,则的范围是 .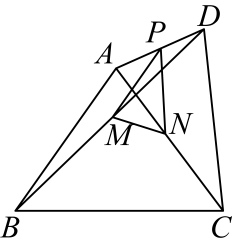 15. 如图,在中,点E , F分别是 , 边的中点,延长至点 , 使 , 以 , 为边向外构造 , 连接交于点 , 连接 . 若 , , 则的长为 .
15. 如图,在中,点E , F分别是 , 边的中点,延长至点 , 使 , 以 , 为边向外构造 , 连接交于点 , 连接 . 若 , , 则的长为 .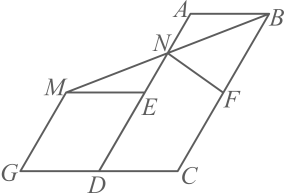
三、解答题
-
16. 如图,△ABC是等边三角形,点D是边BC上的一点,以AD为边作等边△ADE,过点C作CF∥DE交AB于点F.
 (1)、若点D是BC边的中点(如图①) ,求证:EF=CD.(2)、在(1)的条件下直接写出△AEF和△ABC的面积比.(3)、若点D是BC边上的任意一点(除B,C外,如图②) ,那么(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.17. 如图,在△ABC中,D 是边 BC 上一点,E,F,G,H分别是 BD,BC,AC,AD的中点,连结EG,HF.求证:EG,HF 互相平分.
(1)、若点D是BC边的中点(如图①) ,求证:EF=CD.(2)、在(1)的条件下直接写出△AEF和△ABC的面积比.(3)、若点D是BC边上的任意一点(除B,C外,如图②) ,那么(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.17. 如图,在△ABC中,D 是边 BC 上一点,E,F,G,H分别是 BD,BC,AC,AD的中点,连结EG,HF.求证:EG,HF 互相平分.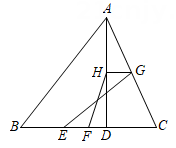 18. 已知E在△ABC内部(如图1),等边三角形ABC的边长为6,等边三角形BDE的边长为4,连结AE和DC.
18. 已知E在△ABC内部(如图1),等边三角形ABC的边长为6,等边三角形BDE的边长为4,连结AE和DC. (1)、求证:AE=DC.(2)、当AE⊥BD时,求CD的长.(3)、将△BDE绕点B旋转一周,F为DC的中点(如图2),求旋转过程中EF的取值范围.
(1)、求证:AE=DC.(2)、当AE⊥BD时,求CD的长.(3)、将△BDE绕点B旋转一周,F为DC的中点(如图2),求旋转过程中EF的取值范围.