人教版初中数学2023-2024学年八年级下学期课时基础练习 18.1平行四边形
试卷更新日期：2024-04-08 类型：同步测试
一、选择题
-
1. 如图，平行四边形的对角线 ， 交于点 ， 已知 ， ， 的周长为15，则的长为（ ）
A、5 B、6 C、7 D、82. 如图，在四边形ABCD中，AD=BC，E，F，G分别是AB，CD，AC的中点.若∠DAC=20°，∠ACB=66°，则∠FEG的度数为（ ）
A、18° B、21° C、22° D、23°3. 如图，在平面直角坐标系xOy中，四边形ABCO是平行四边形，若A，C两点的坐标分别为(3，0)，(1，2)，则▱ABCO的周长为（ ）
A、 B、 C、4 D、4. 两条平行线之间的距离是指（ ）A、两条平行线中，从一条直线上任意一点到另一条直线的垂线段 B、两条平行线中，从一条直线上任意一点到另一条直线的垂线段的长度 C、两条平行线中，从一条直线上任意一点到另一条直线的垂线的长度. D、两条平行线中，从一条直线上任意一点到另一条直线上的一点间线段的长度5. 如图，已知▱ABCD，点 E，F 在对角线AC 上，且AE=CF，连结 DE，DF，BE，BF.求证：四边形DEBF 为平行四边形.以下是排乱的证明过程：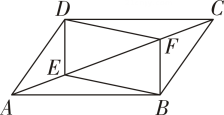
①∴四边形DEBF 为平行四边形.
②∵四边形ABCD为平行四边形，∴OD=OB，OA=OC.
③连结 BD，交 AC 于点O.
④∵AE=CF，∴OA-AE=OC-CF，即OE=OF.
证明步骤正确的顺序是 （ ）
A、①②③④ B、③④②① C、③②④① D、④③②①6. 如图，E是▱ABCD的边 AD 延长线上一点，连结BE，CE，BD，BE 交 CD 于点F.添加以下条件，不能判定四边形 BCED为平行四边形的是 （ ）
A、∠ABD=∠DCE B、DF=CF C、∠AEB=∠BCD D、.∠AEC=∠CBD7. 如图，在△ABC中，D是AB 的中点，E，F在AC 上，且AE=EF，BC=CF.若∠A=25°，∠ADE=10°，则∠ABC的度数为 （ ）
A、35° B、40° C、45° D、50°8. 如图，在▱ABCD中，BE⊥CD，BF⊥AD，∠EBF=45°.若CE=3，DF=1，则▱ABCD的面积为（ ）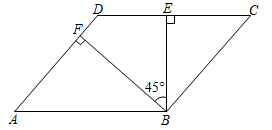
A、 B、 C、 D、9. 如图，两条宽度分别为1和2的长方形纸条交叉放置，重叠部分为四边形ABCD.若AB+BC=6，则四边形ABCD的面积为 （ ）
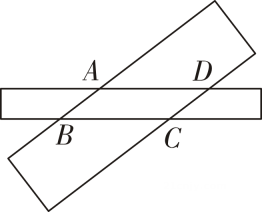A、4 B、2 C、8 D、610. 如图，点A在平行四边形的对角线上，则图中两个阴影三角形的面积S₁，S₂的大小关系是（ ）
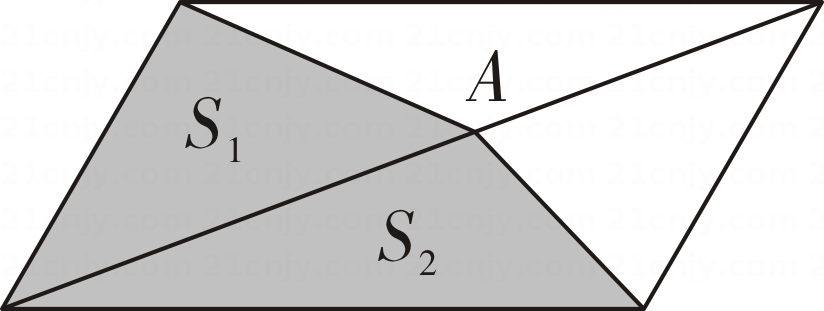A、 B、 C、 D、无法确定二、填空题
-
11. 如图，在▱ABCD中，若AB=4，BC=6，AC的垂直平分线交AD于点E，连结CE，则△CDE的周长为.
12. 如图，在□ABCD中，过对角线 BD上一点 P 作EF∥AB，GH∥AD，与各边的交点分别为E，F，G，H.若▱ABCD的面积为 40，四边形BGPF的面积为 5，四边形 PEDH 的面积为21，则四边形 AGPE 的面积为.
13. 如图，△ABC的周长为 28，点 D，E都在边BC 上，∠ABC 的平分线垂直于 AE，垂足为 Q，∠ACB的平分线垂直于 AD，垂足为 P，连结PQ.若 BC=10，则PQ的长是.
14. 如图，在▱ABCD中，E为CD的中点，连结AE，过点 B作BF⊥AE，垂足为 F.若AD=AE=1，∠DAE=30°，则EF的长为.
15. 如图，在▱ABCD中，AC是对角线，∠ACD=90°，E 是BC的中点，AF平分∠BAC，连结CF，EF.若CF ⊥AF，AB=5，BC=13，则EF的长为
三、解答题
-
16. 如图，在平面直角坐标系中，四边形ABCD是平行四边形，A(-3，0)，B(3，0) ，C(0，4)，连结OD，点E是线段0D的中点．
(1)、求点E和点D的坐标．(2)、平面内是否存在一点N，使以C，D，E，N为顶点的四边形是平行四边形？若存在，请求出点N的坐标；若不存在，请说明理由．17. 如图，在ABCD中，点P是对角线AC上一动点，过点P作PM∥DC，且PM=DC，连结BM，CM，BP，PD．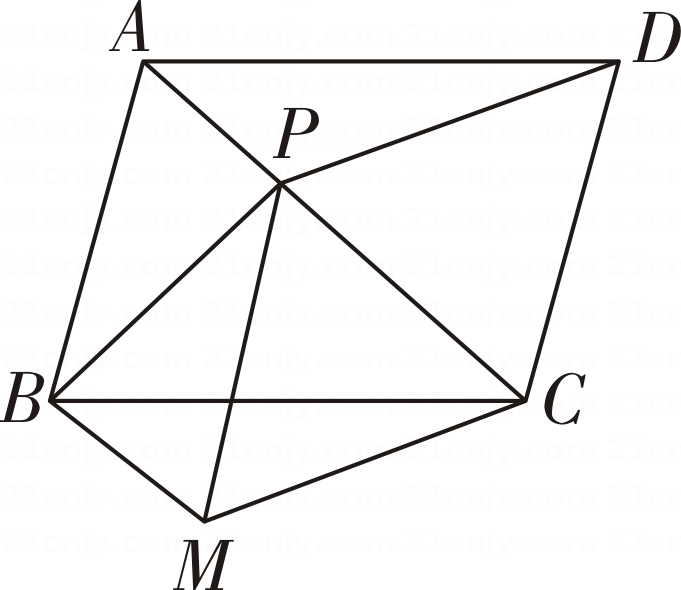
(1)、求证：△ADP≌△BCM；(2)、若PA=PC，设△ABP的面积为S，四边形BPCM的面积为T，求的值.18. 如图，在△ABC中，AB=AC，D，E分别为边AB，AC的中点，连结DE，BE，F，G，H分别为BE，DE，BC的中点，连结FG，FH.
(1)、求证：FG=FH，(2)、若∠A=90°，求证：FG⊥FH.(3)、若∠A=80°，求∠GFH的度数.四、综合题
