新疆维吾尔自治区新疆生产建设兵团2024年中考数学模拟试卷(二)
试卷更新日期:2024-04-08 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、4 B、-4 C、 D、2. 如图所示的三视图表示的几何体是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 某校在体育健康测试中,有8名男生“引体向上”的成绩(单位:次)分别是:14,12,8,9,16,10,12,7,这组数据的中位数和众数分别是( )A、10,12 B、12,11 C、12,12 D、11,125. 不等式组 的整数解有( )A、0个 B、1个 C、2个 D、3个6. 某乡镇决定对一段长6 000米的公路进行修建改造.根据需要,该工程在实际施工时增加了施工人员,每天修健的公路比原计划增加了50%,结果提前4天完成任务.设原计划每天修建x米,那么下面所列方程中正确的是( )A、 B、 C、 D、7. 如图,在平面直角坐标系中,直线 和 相交于点 ,则不等式 的解集为( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 某校在体育健康测试中,有8名男生“引体向上”的成绩(单位:次)分别是:14,12,8,9,16,10,12,7,这组数据的中位数和众数分别是( )A、10,12 B、12,11 C、12,12 D、11,125. 不等式组 的整数解有( )A、0个 B、1个 C、2个 D、3个6. 某乡镇决定对一段长6 000米的公路进行修建改造.根据需要,该工程在实际施工时增加了施工人员,每天修健的公路比原计划增加了50%,结果提前4天完成任务.设原计划每天修建x米,那么下面所列方程中正确的是( )A、 B、 C、 D、7. 如图,在平面直角坐标系中,直线 和 相交于点 ,则不等式 的解集为( ) A、 B、 C、 D、8. 如图,在Rt△ABC中,∠BAC=90°,以点A为圆心,以AB长为半径作弧交BC于点D,再分别以点B,D为圆心,以大于 BD的长为半径作弧,两弧交于点P,作射线AP交BC于点E,若AB=3,AC=4,则CD=( )
A、 B、 C、 D、8. 如图,在Rt△ABC中,∠BAC=90°,以点A为圆心,以AB长为半径作弧交BC于点D,再分别以点B,D为圆心,以大于 BD的长为半径作弧,两弧交于点P,作射线AP交BC于点E,若AB=3,AC=4,则CD=( )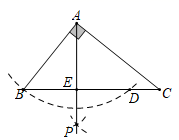 A、 B、 C、 D、9. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2 ,CD⊥AB于点D.点P从点A出发,沿A→D→C的路径运动,运动到点C停止,过点P作PE⊥AC于点E,作PF⊥BC于点F.设点P运动路程为x,四边形CEPF的面积为y,则能反映y与x之间函数关系图象是( )
A、 B、 C、 D、9. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2 ,CD⊥AB于点D.点P从点A出发,沿A→D→C的路径运动,运动到点C停止,过点P作PE⊥AC于点E,作PF⊥BC于点F.设点P运动路程为x,四边形CEPF的面积为y,则能反映y与x之间函数关系图象是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
10. 在函数 中,自变量 的取值范围是.11. 有一人感染了传染性很强的病毒,经过两轮传染后共有625人患病,每轮传染中平均一人传染人.12. 如图,AB是⊙O的直径,AC是弦, , .若用扇形 (图中阴影部分)围成一个圆锥的侧面,则这个圆锥底面圆的半径是.
 13. 如图①是长方形纸带, ,将纸带沿 折叠成图②,再沿 折叠成图③,则图③中的 的度数是.
13. 如图①是长方形纸带, ,将纸带沿 折叠成图②,再沿 折叠成图③,则图③中的 的度数是. 14. 对于一元二次方程 ,若 ,则有 , .方程 …①, …②所有根之和为.15. 如图,动点M在边长为2的正方形ABCD内,且AM⊥BM,P是CD边上的一个动点,E是AD边的中点,则线段PE+PM的最小值为.
14. 对于一元二次方程 ,若 ,则有 , .方程 …①, …②所有根之和为.15. 如图,动点M在边长为2的正方形ABCD内,且AM⊥BM,P是CD边上的一个动点,E是AD边的中点,则线段PE+PM的最小值为.
三、解答题
-
16. 计算:17. 先化简,再求值: ,其中 .18. 已知反比例函数 的图象与一次函数 的图象交于点 .(1)、分别求出这两个函数的解析式;(2)、判断 是否在一次函数 的图象上并说明原因.19. 某课外实践小组的同学们为了解去年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
月均用水
量
频数(户)
频率
6
0.12
0.24
16
0.32
10
0.20
4
2
0.04

解答以下问题:
(1)、表中 , ;(2)、把频数分布直方图补充完整;(3)、若该小区有1500户家庭,根据调查数据估计,该小区月均用水量超过 的家庭大约有多少户?(4)、若从样本里用水量超过20的家庭中,随机抽取两户,求出“家庭月用水量恰好有一户不多于25”的概率.20. 如图,某数学兴趣小组为测量一棵古树的高度,在距离古树A点处测得古树顶端D的仰角为30°,然后向古树底端C步行20米到达点B处,测得古树顶端D的仰角为 ,且点A、B、C在同一直线上,求古树CD的高度.(结果保留根号)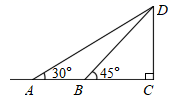 21. 快车和慢车分别从A市和B市两地同时出发,匀速行驶,先相向而行,慢车到达A市后停止行驶,快车到达B市后,立即按原路原速度返回A市(调头时间忽略不计),结果与慢车同时到达A市.快、慢两车距B市的路程y1、y2(单位:km)与出发时间x(单位:h)之间的函数图象如图所示.
21. 快车和慢车分别从A市和B市两地同时出发,匀速行驶,先相向而行,慢车到达A市后停止行驶,快车到达B市后,立即按原路原速度返回A市(调头时间忽略不计),结果与慢车同时到达A市.快、慢两车距B市的路程y1、y2(单位:km)与出发时间x(单位:h)之间的函数图象如图所示. (1)、A市和B市之间的路程是km;(2)、求a的值,并解释图中点M的横坐标、纵坐标的实际意义;(3)、快车与慢车迎面相遇以后,再经过多长时间两车相距20 km?22. 如图, 是⊙ 的直径,弦 ,垂足为 ,连接 .过 上一点 作 交 的延长线于点 ,连接 交 于点 ,且 .
(1)、A市和B市之间的路程是km;(2)、求a的值,并解释图中点M的横坐标、纵坐标的实际意义;(3)、快车与慢车迎面相遇以后,再经过多长时间两车相距20 km?22. 如图, 是⊙ 的直径,弦 ,垂足为 ,连接 .过 上一点 作 交 的延长线于点 ,连接 交 于点 ,且 .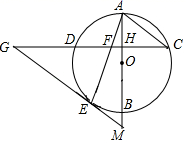 (1)、求证: 是⊙ 的切线;(2)、延长 交 的延长线于点 ,若 , ,求 的长.23. 已知,如图,抛物线 的顶点为 ,经过抛物线上的两点 和 的直线交抛物线的对称轴于点 .
(1)、求证: 是⊙ 的切线;(2)、延长 交 的延长线于点 ,若 , ,求 的长.23. 已知,如图,抛物线 的顶点为 ,经过抛物线上的两点 和 的直线交抛物线的对称轴于点 . (1)、求抛物线的解析式和直线 的解析式.(2)、在抛物线上 两点之间的部分(不包含 两点),是否存在点 ,使得 ?若存在,求出点 的坐标;若不存在,请说明理由.(3)、若点 在抛物线上,点 在 轴上,当以点 为顶点的四边形是平行四边形时,直接写出满足条件的点 的坐标.
(1)、求抛物线的解析式和直线 的解析式.(2)、在抛物线上 两点之间的部分(不包含 两点),是否存在点 ,使得 ?若存在,求出点 的坐标;若不存在,请说明理由.(3)、若点 在抛物线上,点 在 轴上,当以点 为顶点的四边形是平行四边形时,直接写出满足条件的点 的坐标.