新疆维吾尔自治区新疆生产建设兵团2024年中考数学模拟试卷(一)
试卷更新日期:2024-04-08 类型:中考模拟
一、选择题(本大题共9小题,共45.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 如果零上记作 , 那么零下记作( )A、 B、 C、 D、2. 用含的直角三角尺与直尺按如图所示的方式摆放,则的度数是( )
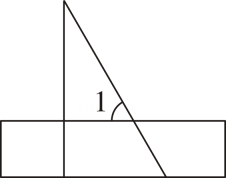 A、
A、
B、
C、
D、3. 一个几何体的三视图如图所示,则这个几何体是( ) A、直三棱柱
A、直三棱柱
B、直三棱锥
C、直四棱柱
D、直四棱锥4. 下列计算正确的是( )A、 B、 C、 D、5. 若关于的一元二次方程有两个不相等的实数根,则的取值范围是( )A、 B、且 C、且 D、6. 关于二次函数的图象与性质,下列结论正确的是( )A、函数图象的顶点坐标为
B、当时,随的增大而增大
C、二次函数的图象与轴有两个交点
D、二次函数的图象可由经过平移得到7. 下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:甲
乙
丙
丁
平均数( )
183
183
182
182
方差
5.7
3.5
6.7
8.6
要从中选择一名发挥稳定的运动员去参加比赛,应该选择( )
A、甲 B、乙 C、丙 D、丁8. 如图,在中, , , 是的角平分线,过点作交边于点若 , 则图中阴影部分面积为( ) A、 B、 C、 D、9. 中国结寓意美满团圆,中间的图案都是小正方形按一定规律组成,其中第个图形共有正方形个,第个图形共有正方形个则第个图形中正方形的总个数为( )
A、 B、 C、 D、9. 中国结寓意美满团圆,中间的图案都是小正方形按一定规律组成,其中第个图形共有正方形个,第个图形共有正方形个则第个图形中正方形的总个数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共30.0分)
-
10. 已知点关于原点的中心对称点在第三象限,则的取值范围是 .11. 关于的一元二次方程的一个根是 , 则实数的值为 .12. 石墨烯是目前世界上最薄却最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.00000000034米,将这个数用科学记数法表示为 .13. 外观相同的件产品中有两件不合格,现从中随机抽取一件进行检测,抽到不合格产品的概率为 .14. 如图,在菱形ABCD中,对角线AC,BD相交于点O,AC=8,BD=6,点E,F分别为AO,DO的中点,则线段EF的长为 .
 15. 如图,在四边形中, , , , 点在边上以每秒的速度从点向点运动,点在边上,以每秒的速度从点向点运动若、同时出发,当直线在四边形内部截出一个平行四边形时,点运动了 秒
15. 如图,在四边形中, , , , 点在边上以每秒的速度从点向点运动,点在边上,以每秒的速度从点向点运动若、同时出发,当直线在四边形内部截出一个平行四边形时,点运动了 秒
三、解答题(本大题共8小题,共75.0分。解答应写出文字说明,证明过程或演算步骤)
-
16. 计算: .17. 先化简,再求值: , 其中 .18. 如图,在平行四边形中,、是对角线上的两点,且 .
 (1)、求证:≌ .(2)、若平分 , 则四边形的形状是 .19. 如图,小明在处用高米米的测角仪测得旗杆的顶端的仰角为 , 再向旗杆方向前进米到处,又测得旗杆顶端的仰角为 , 请求出旗杆的高.
(1)、求证:≌ .(2)、若平分 , 则四边形的形状是 .19. 如图,小明在处用高米米的测角仪测得旗杆的顶端的仰角为 , 再向旗杆方向前进米到处,又测得旗杆顶端的仰角为 , 请求出旗杆的高. 20. 我市为加快推进生活垃圾分类工作,对分类收集桶实行统一的外型、型号、颜色等,其中,可回收物用蓝色收集桶,有害垃圾用红色收集桶,厨余垃圾用绿色收集桶,其他垃圾用灰色收集桶为了解学生对垃圾分类知识的掌握情况,某校宣传小组就“用过的餐巾纸应投放到哪种颜色的收集桶”在全校随机采访了部分学生,根据调查结果,绘制了如图所示的两幅不完整的统计图.
20. 我市为加快推进生活垃圾分类工作,对分类收集桶实行统一的外型、型号、颜色等,其中,可回收物用蓝色收集桶,有害垃圾用红色收集桶,厨余垃圾用绿色收集桶,其他垃圾用灰色收集桶为了解学生对垃圾分类知识的掌握情况,某校宣传小组就“用过的餐巾纸应投放到哪种颜色的收集桶”在全校随机采访了部分学生,根据调查结果,绘制了如图所示的两幅不完整的统计图.
根据图中信息,解答下列问题:
(1)、此次调查一共随机采访了 名学生,在扇形统计图中,“灰”所在扇形的圆心角的度数为 ;(2)、补全条形统计图要求在条形图上方注明人数;(3)、若该校有名学生,估计该校学生将用过的餐巾纸投放到红色收集桶的人数;(4)、李老师计划从 , , , 四位学生中随机抽取两人参加学校的垃圾分类知识抢答赛,请用树状图法或列表法求出恰好抽中 , 两人的概率.21. 如图,某公园里的四条人行步道围成四边形 , 经测量,点在点的正北方向,点在点的北偏西 , 点在点的正西方向,点在点的东北方向, , , 求的长结果保留根号

