吉林省松原市前郭县三校2024年中考数学一模试卷
试卷更新日期：2024-04-08 类型：中考模拟
一、选择题（12分）
-
1. 下列四个数中，最小的数是（ ）A、﹣3 B、0 C、1 D、﹣22. 如图是由6个相同的小正方体搭成的几何体，它的左视图是（ ）
A、
B、
C、
D、
3. 下列运算正确的是（ ）A、a4•a3＝a12 B、（a3）4＝a7 C、a5+a5＝a10 D、2a2÷a2＝24. 如图，A地到B地有三条路线，由上至下依次记为路线b ， c ， a ， 则从A地到B地的最短路线是c ， 其依据是（ ）
A、两点之间，线段最短 B、两点确定一条直线 C、两点之间，直线最短 D、直线比曲线短5. 如图，直线l1∥l2 ， 一副三角板放置在l1 ， l2之间，一三角板直角边在l1上，三角板斜边在同一直线上，则∠α＝（ ）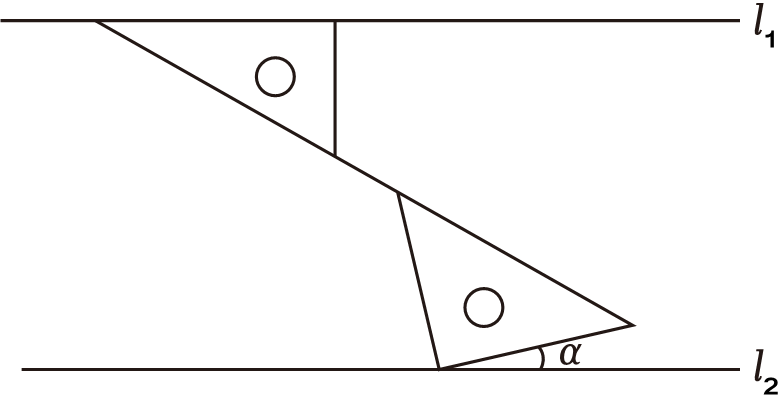
A、10° B、15° C、20° D、25°6. 如图，⊙O是△PAB的外接圆，OC⊥AB ， 连接OB ． 若∠BOC＝50°，则∠APB的度数是（ ）
A、45° B、50° C、55° D、60°二、填空题（每小题3分，共24分）
-
7. 因式分解5a2﹣a＝ ．8. 不等式2x﹣7＞1的解集是 ．9. 如图，该图形绕其中心旋转能与其自身完全重合，则其旋转角最小为度．
10. 一元二次方程x2+4x﹣9＝0的根的判别式的值是 ．11. 某种商品原价每件p元，第一次降价每件减少10元，第二次降价每件打“八折”，则第二次降价后售价是元．12. 如图，AB表示一个窗户，窗户的下端到地面的距离BC＝0.4m，AM和BN表示射入室内的光线，若某一时刻BC在地面的影长CN＝0.5m，AC在地面的影长CM＝2m，则窗户的高度AB为m．
13. 如图，在△ABC中，∠C＝27°，点D在AC的垂直平分线上，将△ABD沿AD翻折后，使点B落在点B1处，线段B1D与AC相交于点E ， 则∠CED＝ ．
14. 在数学跨学科主题活动课上，芳芳用半径为15cm，圆心角为120°的扇形纸板，做了一个圆锥形的生日帽，如图所示，在不考虑接缝的情况下，这个圆锥形生日帽的底面圆的半径是cm．
三、解答题（每小题5分，共20分）
-
15. 先化简，再求. ，其中x＝ ．16. 如图，点E、B在AD上，已知AE＝DB ， AC＝DF ， ∠A＝∠D ， 求证：△ABC≌△DEF ．
17. 某校开设智能机器人编程的校本课程，购买了A、B两种型号的机器人模型．已知A型机器人模型的单价比B型机器人模型的单价多200元，购买5台A型机器人模型的费用比购买7台B型机器人模型的费用多400元，求A型、B型机器人模型的单价分别是多少元？18. 为落实“双减”政策，充分利用好课后服务时间，某校成立了陶艺、园艺、厨艺3个活动小组，分别用卡片A、B、C表示，现有甲、乙两位同学积极报名参加，其中一名同学随机抽取1张后，放回并混在一起，另一名同学再随机抽取1张，用画树状图或列表的方法求甲、乙两位同学中至少有一名参加园艺活动小组的概率．四、解答题（每小题7分，共28分）
-
19. 图①、图②均是5×5的正方形网格，小正方形的边长均为1，每个小正方形的顶点称为格点，线段AB的端点均在格点上．在图①、图②中，只用无刻度的直尺，在给定的网格中，按下列要求作图．
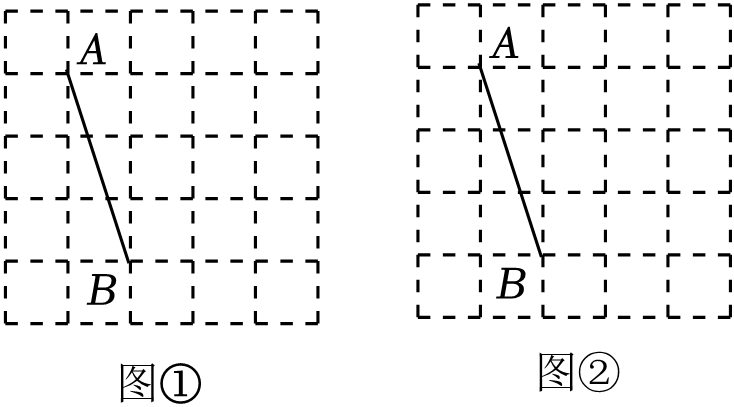(1)、线段AB的长为；(2)、在图①中，以线段AB为腰画一个等腰钝角三角形ABC；(3)、在图②中，以线段AB为边画一个轴对称四边形ABEF ， 使其面积为8．20. 已知蓄电池的电压为定值，使用蓄电池时，电流I（单位：A）与电阻R（单位：Ω）之间的函数关系式为 ， 如图．
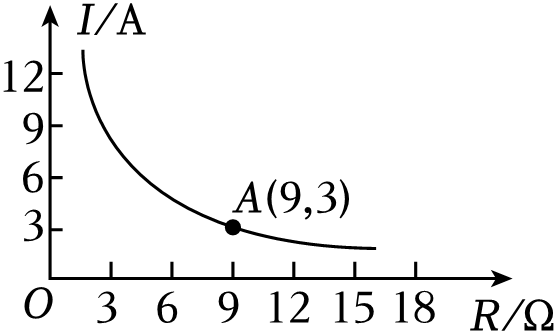(1)、求蓄电池的电压是多少；(2)、如果电流不超过12A ， 求电阻应控制的范围．21. 如图1是一台电脑支架，图2是其侧面示意图，AB ， BC可分别绕B ， C转动，测量知AB＝10cm ， BC＝6cm ， 当AB ， BC转动到∠ABC＝90°时，∠BCD＝37°时，求点A到CD的距离．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）
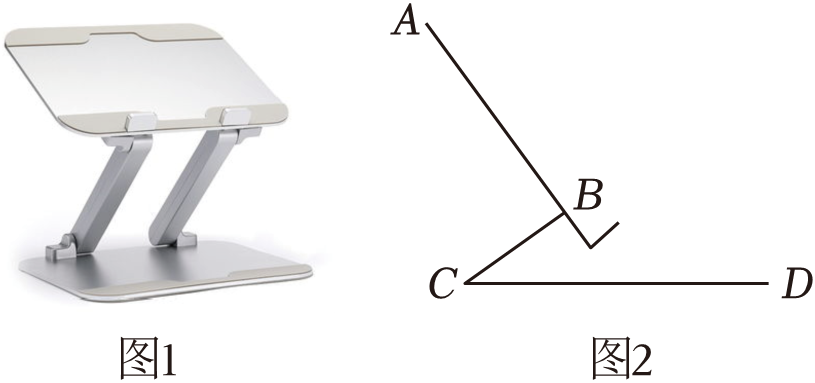22. 为号召学生积极实践创新，创设浓郁学科学氛围，活跃校园科技生活，我校开展了第十一届科技节．学校随机抽取了部分学生对科技节“最喜欢的活动”进行调查：A ． 中国古代科技发明；B ． 创意机器人；C ． 科技改变生活；D ． 立体模型制作．并将调查结果绘制成了两幅统计图，请你根据图中提供的信息回答以下问题：
(1)、本次调查共调查了名学生；(2)、请你补全条形统计图；(3)、计算扇形统计图中“立体模型制作”部分所对应的圆心角度数为°，“中国古代科技发明”部分所占的百分比是；(4)、我校共有2800名学生，估计最喜欢“科技改变生活”和“立体模型制作”的学生大约有多少名？五、解答题（每小题8分，共16分）
-
23. 我市莲池区开展了“阳光体育，强身健体”系列活动，小明积极参与，他每周末和哥哥一起练习赛跑．哥哥先让小明跑若干米 ， 哥哥追上小明后，小明的速度降为原来的一半，已知他们所跑的路程y（m）与哥哥跑步的时间x（s）之间的函数图象如图．
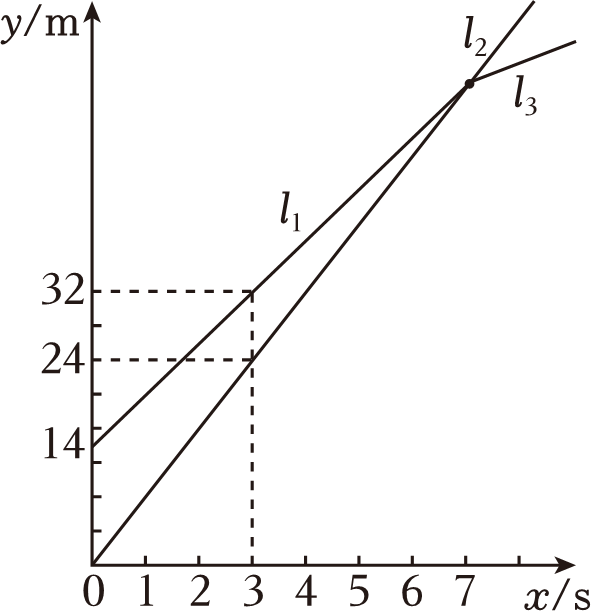(1)、哥哥的速度是m/s，哥哥让小明先跑了米，小明后来的速度为m/s．(2)、哥哥跑几秒时，哥哥追上小明？(3)、求哥哥跑几秒时，两人相距10米？24.(1)、【教材呈现】华师版八年级上册教材第69页的部分内容．例4 如图13.2.13，在△ABC中，D是边BC的中点，过点C画直线CE ， 使CE∥AB ， 交AD的延长线于点E ． 求证：AD＝ED ．
证明：∵CE∥AB（已知），
请根据教材内容，结合图①，补全证明过程．
(2)、【结论应用】如图②，在平行四边形ABCD中，点E是边AD的中点，连结CE ， 线段CE与BA边的延长线交于点F ， 点P、Q分别在线段CE、EF上，且CP＝FQ ．
求证：四边形APDQ是平行四边形．
(3)、如图③，在矩形ABCD中，AB＝2，AD＝4，分别取AB、CD边的中点E、F ， 连结EF ， 经过线段EF中点O任意作一条直线l ， 作点B关于直线l的对称点P ， 连结PE、PO、PF ， 过点E作PF的平行线交PO的延长线于点Q ， 连结FQ ， 得到四边形PEQF ． 则四边形PEQF面积的最大值为 ．六、解答题（每小题10分，共20分）
-
25. 如图①所示，在等腰直角三角形ABC中，∠BAC＝90°，AC＝8cm ， AD⊥BC于点D ， 点P从点A出发，沿A→C方向以1cm/s的速度运动到点C停止，在运动过程中，过点P作PQ∥AB交BC于点Q ， 以线段PQ为边作等腰直角三角形PQM ， 且∠PQM＝90°（点M ， C位于PQ异侧），设点P的运动时间为x（s），△PQM与△ADC重叠部分的面积为y（cm2）．
(1)、如图②，当点M落在AB上时，x＝；(2)、求点M落在AD上时x的值；(3)、若M点在AD下方时，求重叠部分面积y与运动时间x的函数表达式．26. 如图，一次函数与y轴交于点A ， 与x轴交于点B ， 抛物线经过点A、B ， 并与x轴交于另一点C ．
(1)、点A的坐标是 ， 点B的坐标是；(2)、求抛物线的解析式；(3)、在直线AB下方的抛物线上有一个点D ， 求这个四边形ACBD面积的最大值，并写出点D坐标；(4)、在x轴上有一个动点P（m ， 0），当线段OA绕点P逆时针旋转90°后得到线段MN ． 当线段MN与抛物线只有一个公共点时，请直接写出m的取值范围．