湖南省岳阳市汩罗市2023-2024学年九年级下学期开学考试数学试卷
试卷更新日期:2024-04-08 类型:开学考试
一、选择题(每小题3分,共24分)
-
1. 关于 的叙述不正确的是( )A、 =2 B、面积是8的正方形的边长是 C、 是有理数 D、在数轴上可以找到表示 的点2. 一个整数用科学记数法表示为 , 则原数中“0”的个数为( )A、4 B、6 C、7 D、103. 下面四个手机应用图标中,属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列计算中,结果是a7的是( )A、 B、 C、 D、5. 为考察甲、乙、丙、丁四种小麦的长势,在同一时期分别从中随机抽取部分麦苗,获得苗高(单位:)的平均数与方差为: , ; , .则麦苗长得又高又整齐的是( )A、甲 B、乙 C、丙 D、丁6. 下列命题是真命题的是()A、如果|a|=1,那么a=1 B、一组对边平行的四边形是平行四边形 C、如果a是有理数,那么a是实数 D、对角线相等的四边形是矩形7. 如图,两个边长相等的正方形ABCD和EFGH,正方形EFGH的顶点E固定在正方形ABCD的对称中心位置,正方形EFGH绕点E顺时针方向旋转,设它们重叠部分的面积为S,旋转的角度为θ,S与θ的函数关系的大致图象是( )
4. 下列计算中,结果是a7的是( )A、 B、 C、 D、5. 为考察甲、乙、丙、丁四种小麦的长势,在同一时期分别从中随机抽取部分麦苗,获得苗高(单位:)的平均数与方差为: , ; , .则麦苗长得又高又整齐的是( )A、甲 B、乙 C、丙 D、丁6. 下列命题是真命题的是()A、如果|a|=1,那么a=1 B、一组对边平行的四边形是平行四边形 C、如果a是有理数,那么a是实数 D、对角线相等的四边形是矩形7. 如图,两个边长相等的正方形ABCD和EFGH,正方形EFGH的顶点E固定在正方形ABCD的对称中心位置,正方形EFGH绕点E顺时针方向旋转,设它们重叠部分的面积为S,旋转的角度为θ,S与θ的函数关系的大致图象是( )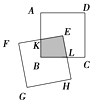 A、
A、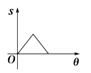 B、
B、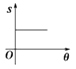 C、
C、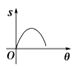 D、
D、 8. 观察下列等式:21=2,22=4,23=8,24=16,25=32,26=64,…,根据这个规律,则21+22+23+24+…+22020的末位数字是( )A、0 B、2 C、4 D、6
8. 观察下列等式:21=2,22=4,23=8,24=16,25=32,26=64,…,根据这个规律,则21+22+23+24+…+22020的末位数字是( )A、0 B、2 C、4 D、6二、填空题(每小题4分,共32分)
-
9. 如果m是最大的负整数,n是绝对值最小的有理数,c是倒数等于它本身的自然数,那么代数式 的值为.10. 分解因式: .11. 关于x的一元二次方程x2+2x+k=0有两个不相等的实数根,则k的取值范围是 .12. 抛物线的顶点坐标是.13. 某药店在防治新型冠状病毒期间,市场上抗病毒药品紧缺的情况下将某药品提价100%,物价部门查处后,限定其提价幅度只能是原价的10%,则该药品现在降价的幅度是.(填百分数)14. 如图,无人机在空中C处测得地面A、B两点的俯角分别为600、450 , 如果无人机距地面高度CD为米,点A、D、E在同一水平直线上,则A、B两点间的距离是米.(结果保留根号)
 15. 我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为a,b,c,则该三角形的面积为S = 现已知△ABC的三边长分别为1,2, ,则△ABC的面积为16. 如图,直线 , 点坐标为(1,0),过点作轴的垂线交直线于点 , 以原点为圆心, 长为半径画弧交轴于点;再过点作轴的垂线交直线于点 , 以原点为圆心,长为半径画弧交轴于点;…,按此做法进行下去,点的坐标为.
15. 我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为a,b,c,则该三角形的面积为S = 现已知△ABC的三边长分别为1,2, ,则△ABC的面积为16. 如图,直线 , 点坐标为(1,0),过点作轴的垂线交直线于点 , 以原点为圆心, 长为半径画弧交轴于点;再过点作轴的垂线交直线于点 , 以原点为圆心,长为半径画弧交轴于点;…,按此做法进行下去,点的坐标为.
三、解答题(本大题共8小题,满分64分.解答应写出必要的文字说明、证明过程或演算步骤.)
-
17. 计算:18. 先化简, , 然后从—1、0、1、2中选择一个合适的数代入求值。19. 如图,一次函数 的图象与反比例函数 ( 为常数且 )的图象交于 , 两点,与 轴交于点 .
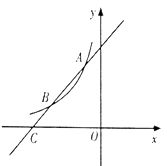 (1)、求此反比例函数的表达式;(2)、若点 在 轴上,且 ,求点 的坐标.20. 中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
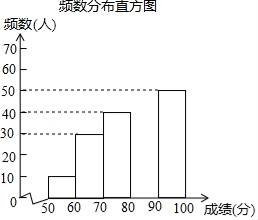
(1)、求此反比例函数的表达式;(2)、若点 在 轴上,且 ,求点 的坐标.20. 中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:频数频率分布表
成绩x(分)
频数(人)
频率
50≤x<60
10
0.05
60≤x<70
30
0.15
70≤x<80
40
n
80≤x<90
m
0.35
90≤x≤100
50
0.25
根据所给信息,解答下列问题:
(1)、m= , n=;(2)、补全频数分布直方图;(3)、这200名学生成绩的中位数会落在分数段;(4)、若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?21. 预防新型冠状病毒期间,某种消毒液A县需要6吨,B县需要8吨,正好C县储备有10吨,D县储备有4吨,市预防新型冠状病毒领导小组决定将这14吨消毒液调往A县和B县, 消毒液的运费价格如下表(单位:元/吨),设从C县调运x吨到A县.起点 \ 终点
A县
B县
C县
60
100
D县
35
70
(1)、求调运14吨消毒液的总运费y关于x的函数关系式.(2)、求出总运费最低的调运方案,最低运费是多少?22. 如图所示,C城市在A城市正东方向,现计划在A、C两城市间修建一条高速公路(即线段AC),经测量,森林保护区的中心P在A城市的北偏东60°方向上,在线段AC上距A城市120km的B处测得P在北偏东30°方向上,已知森林保护区是以点P为圆心,100km为半径的圆形区域,请问计划修建的这条高速公路是否穿越保护区,为什么?(参考数据: ≈1.73)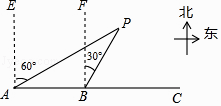 23. 已知正方形ABCD,点M是边AB的中点.
23. 已知正方形ABCD,点M是边AB的中点.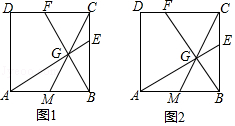 (1)、如图1,点G为线段CM上的一点,且∠AGB=90°,延长AG、BG分别与边BC、CD交于点E、F.
(1)、如图1,点G为线段CM上的一点,且∠AGB=90°,延长AG、BG分别与边BC、CD交于点E、F.①求证:BE=CF;②求证:BE2=BC•CE.
(2)、如图2,在边BC上取一点E,满足BE2=BC•CE,连接AE交CM于点G,连接BG并延长CD于点F,求tan∠CBF的值.24. 如图,已知二次函数 的图象经过点 ,与 轴分别交于点 ,点 .点 是直线 上方的抛物线上一动点.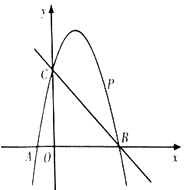 (1)、求二次函数 的表达式;(2)、连接 , ,并把 沿 轴翻折,得到四边形 .若四边形 为菱形,请求出此时点 的坐标;(3)、当点 运动到什么位置时,四边形 的面积最大?求出此时 点的坐标和四边形 的最大面积.
(1)、求二次函数 的表达式;(2)、连接 , ,并把 沿 轴翻折,得到四边形 .若四边形 为菱形,请求出此时点 的坐标;(3)、当点 运动到什么位置时,四边形 的面积最大?求出此时 点的坐标和四边形 的最大面积.