湖南省师大附中教育集团2024年中考数学三检试卷

试卷更新日期：2024-04-08 类型：中考模拟

进入出卷网下载

一、选择题（本大题共10个小题，每小题3分，共30分）

1. 如所示4个图形中，是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 抛物线y=（x﹣1）²+3的对称轴是（）

A、直线x=1 B、直线x=3 C、直线x=﹣1 D、直线x=﹣3

查看试题解析
3. 在双曲线 $y = \frac{k}{x}$ 的任意一支上，y都随x的增大而减小，则k的值可以是（　　）

A、﹣2 B、0 C、2 D、﹣1

查看试题解析

4. 县林业部门考察银杏树苗在一定条件下移植的成活率，所统计的银杏树苗移植成活的相关数据如下表所示：

移植的棵数a	100	300	600	1000	7000	15000
成活的棵数b	84	279	505	847	6337	13581
成活的频率 $\frac{b}{a}$	0.84	0.93	0.842	0.847	0.905	0.905

根据表中的信息，估计银杏树苗在一定条件下移植成活的概率为（精确到0.1）（　　）

A、0.905 B、0.90 C、0.9 D、0.8

查看试题解析

5. 如图，在平面直角坐标系中，△OAB的顶点为O（0，0），A（4，3），B（3，0）．以点O为位似中心，在第三象限内得到与△OAB的位似比为 $\frac{1}{3}$ 的位似图形△OCD ，则点C的坐标为（　　）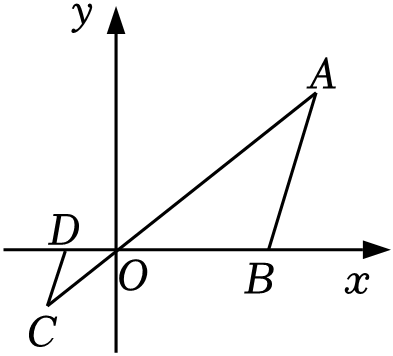

A、（﹣1，﹣1） B、 $(- \frac{4}{3} ， - 1)$ C、 $(- 1 ， - \frac{4}{3})$ D、（﹣2，﹣1）

查看试题解析
6. 如图，在△ABC中，DE∥AB，且 $\frac{C D}{B D}$ ＝ $\frac{3}{2}$ ，则 $\frac{C E}{C A}$ 的值为（　　）

A、 $\frac{3}{5}$ B、 $\frac{2}{3}$ C、 $\frac{4}{5}$ D、 $\frac{3}{2}$

查看试题解析
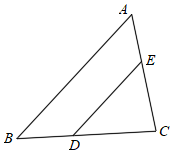7. 已知反比例函数 $y = \frac{- 2}{x}$ 的图象上有点A（2，y₁），B（1，y₂），C（﹣3，y₃），则关于y₁ ， y₂ ， y₃大小关系正确的是（　　）

A、y₁＞y₂＞y₃ B、y₂＞y₁＞y₃ C、y₁＞y₃＞y₂ D、y₃＞y₁＞y₂

查看试题解析
8. 如图，△ABC的内切圆⊙O分别与AB ， BC ， AC相切于点D ， E ， F ，且AD＝3，BE＝2，CF＝4，则△ABC的周长为（　　）

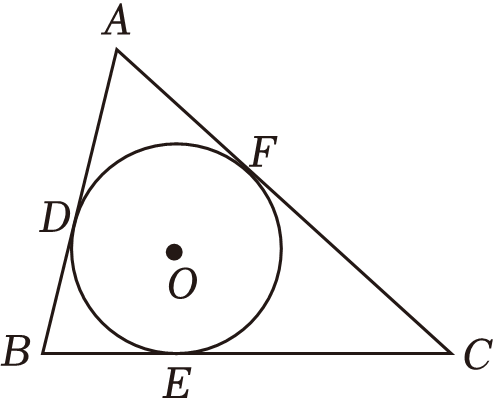A、18 B、17 C、16 D、15

查看试题解析
9. 元旦将至，九（1）班全体学生互赠贺卡，共赠贺卡1980张，问九（1）班共有多少名学生？设九（1）班共有x名学生，那么所列方程为（　　）

A、x²＝1980 B、x（x+1）＝1980 C、 $\frac{1}{2}$ x（x﹣1）＝1980 D、x（x﹣1）＝1980

查看试题解析
10. 如图，在平面直角坐标系中，O为原点，OA＝OB＝3 $\sqrt{5}$ ，点C为平面内一动点，BC＝ $\frac{3}{2}$ ，连接AC ，点M是线段AC上的一点，且满足CM：MA＝1：2．当线段OM取最大值时，点M的坐标是（　　）

A、 $(\frac{3}{5} ， \frac{6}{5})$ B、 $(\frac{3}{5} \sqrt{5} ， \frac{6}{5} \sqrt{5})$ C、 $(\frac{6}{5} ， \frac{12}{5})$ D、 $(\frac{6}{5} \sqrt{5} ， \frac{12}{5} \sqrt{5})$

查看试题解析

二、填空题（本大题共6个小题，每小题3分，共18分）

11. 已知点A（﹣2，b）与B（a ， 3）点关于原点对称，则a+b＝．

查看试题解析
12. 如图，四边形ABCD是圆内接四边形，∠C＝120°，求∠A的度数为度．

查看试题解析
13. 已知扇形的半径为2cm ，圆心角为120°，则此扇形的弧长是cm ．

查看试题解析
14. 如图， $A$ 、 $B$ 、 $C$ 、 $D$ 为一个正多边形的顶点， $O$ 为正多边形的中心，若 $∠ A D B = 20 °$ ，则这个正多边形的边数为.

查看试题解析
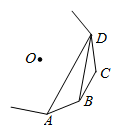15. 如图，在网格中，每个小正方形的边长均为1，每个小正方形的顶点称为格点．点A、B、C三点都在格点上，则 $s i n ∠ A B C =$ ．

查看试题解析
16. 如图，平行于x轴的直线与函数 $y = \frac{k_{1}}{x}$ （k₁＞0，x＞0）和 $y = \frac{k_{2}}{x}$ （k₂＞0，x＞0）的图象分别相交于A ， B两点．点A在点B的右侧，C为x轴上的一个动点，若△ABC的面积为4，则k₁﹣k₂的值为．

查看试题解析

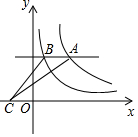
三、解答题（本大题共9个小题，第17、18、19题每题6分，第20、21题每题8分，第22、23题每题9分，第24、25题每题10分，共72分）

17. 计算： $\sqrt{3} t a n 3 0^{°} + {(\frac{1}{2})}^{- 2} + | \sqrt{2} - 1 | + \sqrt[3]{- 64}$ ．

查看试题解析
18. 如图，在平面直角坐标系中，一次函数 $y = - \frac{3}{2} x + b$ 与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 交于A（m ， 6），B（4，﹣3）两点，与y轴交于点C ，连接OA ， OB ．

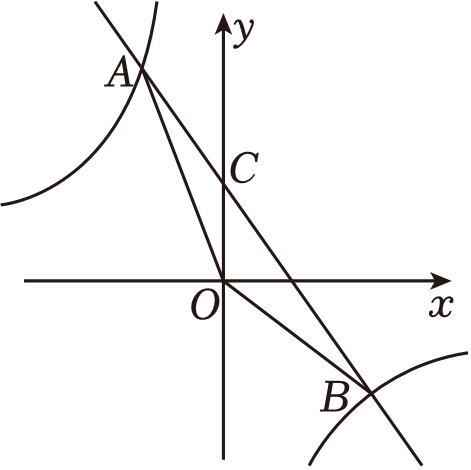(1)、求反比例函数和一次函数的表达式；

(2)、求△AOB的面积．

查看试题解析
19. 如图，灯塔B位于港口A的北偏东58°方向，且A ， B之间的距离为30km ，灯塔C位于灯塔B的正东方向，且B ， C之间的距离为10km ．一艘轮船从港口A出发，沿正南方向航行到达D处，测得灯塔C在北偏东37°方向上，灯塔B到直线AD的距离为BE ．

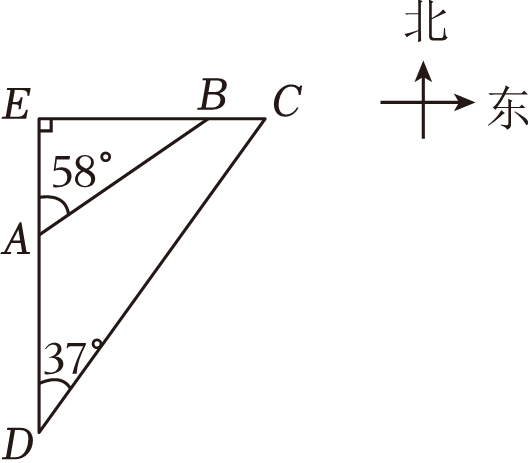(1)、求BE的长；

(2)、求DE的长（结果精确到0.1）．
（参考数据：sin58°≈0.85，cos58°≈0.53，tan58°≈1.60，sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

查看试题解析
20. 为了丰富学生们的课余生活，学校准备开展第二课堂，有四类课程可供选择，分别是“A．书画类、B．文艺类、C．社会实践类、D．体育类”．现随机抽取了七年级部分学生对报名意向进行调查，并根据调查结果绘制了两幅不完整的统计图，请你根据图表信息回答下列问题：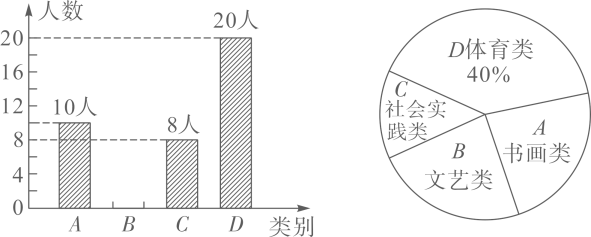

(1)、本次被抽查的学生共有名，扇形统计图中“A．书画类”所占扇形的圆心角的度数为度；

(2)、请你将条形统计图补全；

(3)、若该校七年级共有600名学生，请根据上述调查结果估计该校学生选择“C．社会实践类”的学生共有多少名？

(4)、本次调查中抽中了七（1）班王芳和小颖两名学生，请用列表法或画树状图法求她们选择同一个项目的概率．

查看试题解析
21. 如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于点D ．

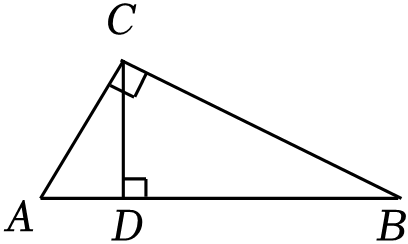(1)、求证：△ADC∽△CDB；

(2)、若AD＝2，BD＝8，求CD ．

查看试题解析
22. 如图，AB ， CD为⊙O的直径，C为⊙O上一点，过点C的切线与AB的延长线交于点P ， ∠ABC＝2∠BCP ，点E是 $\hat{B D}$ 的中点，弦CE ， BD相交于点F ．

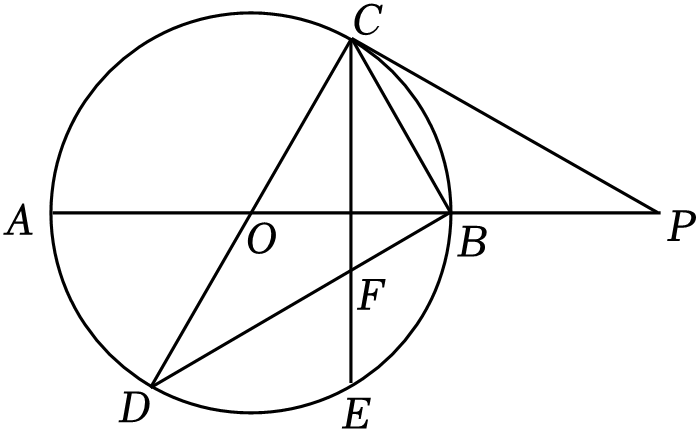(1)、求∠OCB的度数；

(2)、若EF＝3，求⊙O直径的长．

查看试题解析
23. 为纪念爱国诗人屈原，人们有了端午节吃粽子的习俗．下表列出了小欢妈妈、小乐妈妈端午节前在超市购买粽子的数量（单位：个）和付款金额（单位：元）．

豆沙粽数量
肉粽数量
付款金额
小欢妈妈
20
30
270
小乐妈妈
30
20
230

(1)、求豆沙粽和肉粽的单价；

(2)、为进一步提升粽子的销量，超市将两种粽子打包成A ， B两种包装销售，每包都是40个粽子（包装成本忽略不计），每包的销售价格按其中每个粽子的单价合计．A ， B两种包装中分别有m个豆沙粽，m个肉粽，A包装中的豆沙粽数量不超过肉粽的一半．端午节当天统计发现，A ， B两种包装的销量分别为（80﹣4m）包，（4m+8）包，A ， B两种包装的销售总额为17280元，求m的值．

查看试题解析
24. 若两条抛物线相交于A（x₁ ， y₁），B（x₂ ， y₂）两点，并满足y₁﹣kx₁＝y₂﹣kx₂ ，其中k为常数，我们不妨把k叫做这两条抛物线的“依赖系数”．

(1)、若两条抛物线相交于A（﹣2，2），B（﹣4，4）两点，求这两条抛物线的“依赖系数”；

(2)、若抛物线1：y＝2ax²+x+m与抛物线2：y＝ax²﹣x﹣n相交于A（x₁ ， y₁），B（x₂ ， y₂）两点，其中a＞0，求抛物线1与抛物线2的“依赖系数”；

(3)、如图，在（2）的条件下，设抛物线1和2分别与y轴交于C ， D两点，AB所在的直线与y轴交于E点，若点A在x轴上，m≠0，DA＝DC ，抛物线2与x轴的另一个交点为点F ，以D为圆心，CD为半径画圆，连接EF ，与圆相交于G点，求tan∠ECG ．

查看试题解析

	豆沙粽数量	肉粽数量	付款金额
小欢妈妈	20	30	270
小乐妈妈	30	20	230