广东省惠州市尚书实验分校2023-2024学年八年级上册12月月考数学试题
试卷更新日期:2024-04-08 类型:月考试卷
一、选择题(本题共10个小题,每小题3分,共30分)
-
1. 在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 以下列各组数据为三角形的三边,能构成三角形的是( )A、4,8,7 B、3,4,7 C、2,3,7 D、5,2,23. 若一个多边形的每个外角都是 , 则这个多边形的边数为( )A、6 B、8 C、10 D、124. 下列计算正确的是( )A、(ab) 2=a2b2 B、2(a+1)=2a+1 C、a2+a3=a6 D、a6÷a2=a35. 如图,点F、C在上,且 . 若 , 则的长为( )
2. 以下列各组数据为三角形的三边,能构成三角形的是( )A、4,8,7 B、3,4,7 C、2,3,7 D、5,2,23. 若一个多边形的每个外角都是 , 则这个多边形的边数为( )A、6 B、8 C、10 D、124. 下列计算正确的是( )A、(ab) 2=a2b2 B、2(a+1)=2a+1 C、a2+a3=a6 D、a6÷a2=a35. 如图,点F、C在上,且 . 若 , 则的长为( ) A、2 B、5 C、7 D、126. 分式 中的x,y都扩大2倍,则分式的值( )A、不变 B、扩大2倍 C、扩大4倍 D、缩小2倍7. 如图,在中, , 平分 , 交于点 , , 垂足为点 , 若 , 则的长为( )
A、2 B、5 C、7 D、126. 分式 中的x,y都扩大2倍,则分式的值( )A、不变 B、扩大2倍 C、扩大4倍 D、缩小2倍7. 如图,在中, , 平分 , 交于点 , , 垂足为点 , 若 , 则的长为( ) A、 B、 C、 D、8. 已知(a+b)2=49,a2+b2=25,则ab=( )A、24 B、48 C、12 D、29. 如图所示,现要在一块三角形草坪上建一凉亭供大家休息,使凉亭到草坪三个顶点的距离相等,凉亭的位置应选在( )
A、 B、 C、 D、8. 已知(a+b)2=49,a2+b2=25,则ab=( )A、24 B、48 C、12 D、29. 如图所示,现要在一块三角形草坪上建一凉亭供大家休息,使凉亭到草坪三个顶点的距离相等,凉亭的位置应选在( ) A、三条角平分线的交点 B、三条高所在直线的交点 C、三条中线的交点 D、三边的垂直平分线的交点10. 如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则下列四个结论:①PA平分∠BAC;②AS=AR;③QP∥AR;④△BRP≌△CSP,其中结论正确的的序号为( )
A、三条角平分线的交点 B、三条高所在直线的交点 C、三条中线的交点 D、三边的垂直平分线的交点10. 如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则下列四个结论:①PA平分∠BAC;②AS=AR;③QP∥AR;④△BRP≌△CSP,其中结论正确的的序号为( ) A、①②③ B、①②④ C、②③④ D、①②③④
A、①②③ B、①②④ C、②③④ D、①②③④二、填空题(本题共6小题,每题3分,共18分)
-
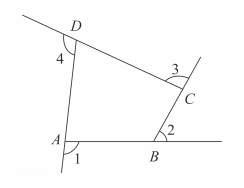
11. 计算: .12. 在中, , , 则的值是 .13. 设ΔABC 三边分别为 a、b、c,其中 a,b 满足 +(a-b-4)2 =0,则第三边 c的取值范围为 .14. 如图是由射线、、、组成的平面图形,则°.
 15. 如图,菱形的边长为 , 点E为边的中点,点P为对角线上一动点,则的最小值为 .
15. 如图,菱形的边长为 , 点E为边的中点,点P为对角线上一动点,则的最小值为 . 16. 如图所示,在△ABC中,AB=6,AC=4,AD是△ABC的中线,若AD的长为偶数,则AD=.
16. 如图所示,在△ABC中,AB=6,AC=4,AD是△ABC的中线,若AD的长为偶数,则AD=.
三、解答题(一)(本大题共4小题,17、18每题4分,19、20每题6分,共20分)
-
17. 计算:18. 已知:如图, , 求证: .
 19. 先化简,再求值: , 其中 , .20. 如图,在中, .
19. 先化简,再求值: , 其中 , .20. 如图,在中, . (1)、用直尺和圆规作的中垂线,交于点D;(要求保留作图痕迹)(2)、连接 , 若 , , 求的周长.
(1)、用直尺和圆规作的中垂线,交于点D;(要求保留作图痕迹)(2)、连接 , 若 , , 求的周长.四、解答题(二)(本大题共3小题,21题8分,22、23每题10分,共28分)
-
21. 中, , 是中点,于 , 于 , 求证: .
 22. 如图,于于F,若 ,
22. 如图,于于F,若 ,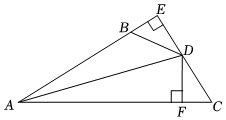 (1)、求证:平分;(2)、已知 , 求的长.
(1)、求证:平分;(2)、已知 , 求的长.五、解答题(三)(本大题共2小题,每题12分,共24分)
-
23. 小明在学习有关整式的知识时,发现一个有趣的现象:关于的多项式 , 由于 , 所以当取任意一对互为相反数的数时,多项式的值是相等的,例如,当 , 即或时,的值均为3;当 , 即或-1时,的值均为6,于是小明给出一个定义:关于的多项式,若当取任意一对互为相反数的数时,该多项式的值相等,就称该多项式关于对称,例如关于对称.
请结合小明的思考过程,运用此定义解决下列问题:
(1)、多项式关于对称;(2)、若关于的多项式关于对称,求的值;(3)、若整式关于对称,试直接写出实数的值.24. 在△ABC中,∠ABC与∠ACB的平分线相交于点P. (1)、如图①,若∠BPC=α,则∠A=;(用α的代数式表示,请直接写出结论)(2)、如图②,作△ABC外角∠MBC、∠NCB的角平分线交于点Q,试探究∠Q与∠BPC之间的数量关系,并说明理由;(3)、如图③,延长线段CP、QB交于点E,△CQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.
(1)、如图①,若∠BPC=α,则∠A=;(用α的代数式表示,请直接写出结论)(2)、如图②,作△ABC外角∠MBC、∠NCB的角平分线交于点Q,试探究∠Q与∠BPC之间的数量关系,并说明理由;(3)、如图③,延长线段CP、QB交于点E,△CQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.