广西壮族自治区钦州市浦北县2023-2024学年八年级下学期3月月考数学试题

试卷更新日期：2024-04-08 类型：月考试卷

进入出卷网下载

一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中只有一项是符合要求的，请用2B铅笔把答题卡上对应题目的答案标号涂黑．）

1. 下列二次根式是最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{7}$ C、 $\sqrt{8}$ D、 $\sqrt{0.3}$

查看试题解析
2. 下列各组数据中的三个数作为三角形的边长，其中能构成直角三角形的是（）

A、 $\sqrt{3}$ 、 $\sqrt{4}$ 、 $\sqrt{5}$ B、2、3、4 C、6、7、8 D、9、12、15

查看试题解析
3. 式子 $\sqrt{n + 1}$ 在实数范围内有意义，则n的取值范围为（）

A、 $n \leq - 1$ B、 $n < 1$ C、 $n \geq - 1$ D、 $n > 1$

查看试题解析
4. 下列计算错误的是（　　）

A、 $4 \sqrt{3} + 2 \sqrt{3} = 6 \sqrt{3}$ B、 $4 \sqrt{3} - 2 \sqrt{3} = 2 \sqrt{3}$ C、 $4 \sqrt{3} \div 2 \sqrt{3} = 2$ D、 $4 \sqrt{3} \times 2 \sqrt{3} = 8 \sqrt{3}$

查看试题解析
5. 如图，在边长为1的正方形网格中，点A ， B ， C均在格点上，则对 $△ A B C$ 的形状描述最准确的是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰直角三角形

查看试题解析
6. 用代数式表示“一个圆柱的高为5，体积为V ．求它的底面半径r”正确的是（）

A、 $\sqrt{\frac{V}{5 π}}$ B、 $\frac{V}{5 π}$ C、 $\frac{\sqrt{V}}{5 π}$ D、 $\frac{V}{\sqrt{5 π}}$

查看试题解析
7. 若直角三角形一条直角边长为6，斜边长为10，则斜边上的高是（　　）

A、 $\frac{12}{5}$ B、 $\frac{24}{5}$ C、5 D、10

查看试题解析
8. 已知 $a < b$ ，且 $a b \neq 0$ ，化简二次根式 $\sqrt{- a^{3} b}$ 的结果是（）

A、 $- a \sqrt{- a b}$ B、 $- a \sqrt{a b}$ C、 $a \sqrt{a b}$ D、 $a \sqrt{- a b}$

查看试题解析
9. 如图，点O为数轴的原点，点A和B分别对应的实数是-1和1．过点B作 $B C ⊥ A B$ ，以点B为圆心，OB长为半径画弧，交BC于点D；以点A为圆心，AD长为半径画弧，交数轴的正半轴于点E ，则点E对应的实数是（）

A、 $\sqrt{5} - 1$ B、 $\sqrt{5}$ C、 $\sqrt{3}$ D、 $\sqrt{3} - 1$

查看试题解析
10. 如图所示，将一根 $24 c m$ 的筷子，置于底面直径为 $15 c m$ ，高 $8 c m$ 的圆柱形水杯中，设筷子露在杯子外面的长度 $h c m$ ，则h的取值范围是（）

A、 $h \leq 17 c m$ B、 $h \geq 8 c m$ C、 $15 c m \leq h \leq 16 c m$ D、 $7 c m \leq h \leq 16 c m$

查看试题解析
11. 已知 $0 < x < 1$ ，且 $x + \frac{1}{x} = 7$ ，则 $\sqrt{x} - \frac{1}{\sqrt{x}}$ 的值为（）

A、 $- \sqrt{10}$ B、 $- \sqrt{5}$ C、 $\sqrt{5}$ D、 $\sqrt{10}$

查看试题解析
12. 如图，在赵爽弦图中，已知直角三角形的短直角边长为 $a$ ，长直角边长为 $b$ ，大正方形的面积为20，小正方形的面积为4，则 $a b$ 的值是（）

A、10 B、9 C、8 D、7

查看试题解析

二、填空题（本大题共6小题，每小题2分，共12分．）

13. 计算： $\sqrt{{(- 2)}^{2}}$ ＝．

查看试题解析
14. 命题“两直线平行，同位角相等．”的逆命题是．

查看试题解析
15. 比较大小： $3 \sqrt{2}$ $2 \sqrt{5}$ （填“＞”或“＜”或“=”）.

查看试题解析
16. 已知 $\sqrt{20 n}$ 是整数，则满足条件的最小正整数n为

查看试题解析
17. 如图， $∠ C A B = 45 °$ ，点D在射线AB上，且 $A D = 4$ ，点P在射线AC上运动，当 $△ A D P$ 是直角三角形时，PD的长为．

查看试题解析
18. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $∠ A B C = 30 °$ ， $A C = 3$ ．点D为 $△ A B C$ 外一点，满足 $∠ B A D = 15 °$ ， $∠ A B D = 30 °$ ，则 $△ A B D$ 的面积是．

查看试题解析

三、解答题（本大题共8小题，共72分．解答应写出文字说明、证明过程或演算步骤．）

19. 化简：

(1)、 $\sqrt{100}$ ；

(2)、 $\sqrt{16 x}$ ；

(3)、 $\frac{\sqrt{a^{3} b}}{2}$ （a≥0，b≥0）

查看试题解析
20. 计算：

(1)、 $\sqrt{12} - \sqrt{18} \times \sqrt{\frac{3}{2}}$ ；

(2)、 $(4 \sqrt{2} - 3 \sqrt{6}) \div 2 \sqrt{2}$ ．

查看试题解析
21. 已知 $x = \sqrt{3} - \sqrt{7}$ ， $y = \sqrt{7} + \sqrt{3}$ ，求 ${(x + y)}^{2} - 3 x y$ 的值．

查看试题解析
22. 如图，在△ABC中，AD⊥BC，垂足为D，∠B=60°，∠C=45°．

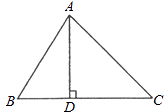(1)、求∠BAC的度数．

(2)、若AC=2，求AD的长．

查看试题解析
23. 如图，学校有一块三角形空地 $A B C$ ，计划将这块三角形空地分割成四边形 $A B D E$ 和 $△ E D C$ ，分别摆放“秋海棠”和“天竺葵”两种不同的花卉，经测量， $∠ E D C = 90 °$ ， $D C = 3$ ， $C E = 5$ ， $B D = 7$ ， $A B = 8$ ， $A E = 1$ ，求四边形 $A B D E$ 的面积．

查看试题解析
24. 木工师傅为了让直尺经久耐用，常常在直尺的直角顶点与斜边之间加一根小木条，如左图所示，右图为其示意图．若 $∠ B A C = 90 °$ ，线段 $A B$ 的长为15cm，线段 $A C$ 的长为20cm，试求出小木条 $A D$ 的最短长度．

查看试题解析
25. 先阅读材料，然后回答问题．

(1)、小张同学在研究二次根式的化简时，遇到了一个问题：化简 $\sqrt{5 - 2 \sqrt{6}}$ ．
经过思考，小张解决这个问题的过程如下：
$\sqrt{5 - 2 \sqrt{6}} = \sqrt{2 - 2 \sqrt{2 \times 3} + 3}$ ①
$= \sqrt{(\sqrt{2})^{2} - 2 \sqrt{2} \times \sqrt{3} + (\sqrt{3})^{2}}$ ②
$= \sqrt{(\sqrt{2} - \sqrt{3})^{2}}$ ③
$= \sqrt{2} - \sqrt{3}$ ． ④
在上述化简过程中，第步出现了错误，化简的正确结果为；

(2)、请根据你从上述材料中得到的启发，化简 $\sqrt{3 - 2 \sqrt{2}} =$ ；

(3)、在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $B C = 1$ ， $A C = 2 + \sqrt{3}$ ，求 $A B$ 的长．

查看试题解析
26. 如图，四边形 $C E D F$ ， $∠ C E D = ∠ E D F = ∠ D F C = ∠ F C E = 90 °$ ， $C E = D E = D F = C F$ ， A是边DE上一点，过点C作 $B C ⊥ A C$ 交 $D F$ 延长线于点B ．

(1)、求证： $B D = A E + C E$ ；

(2)、设 $△ A C E$ 三边分别为a、b、c ，利用此图证明勾股定理．

查看试题解析