广西壮族自治区钦州市浦北县2024年中考一模数学模拟试题

试卷更新日期：2024-04-08 类型：中考模拟

进入出卷网下载

一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中只有一项是符合要求的，请用2B铅笔把答题卡上对应题目的答案标号涂黑．）

1. 如图是一个几何体的展开图，则该几何体是（）

A、三棱柱 B、三棱锥 C、四棱锥 D、四棱柱

查看试题解析
2. 下列说法中，正确的是（）

A、所有的正方形都相似 B、所有的菱形都相似 C、底边相等的两个等腰三角形相似 D、对角线相等的两个矩形相似

查看试题解析
3. 下列关系式中，是反比例函数的是（）

A、 $y = 2 x + 1$ B、 $y = x^{2} - 4$ C、 $y = \frac{4}{x}$ D、 $y = \frac{x}{2}$

查看试题解析
4. 长方形的正投影不可能是（）

A、正方形 B、长方形 C、线段 D、梯形

查看试题解析
5. 如图，小兵同学从A处出发向正东方向走x米到达B处，再向正北方向走到C处，已知 $∠ B A C = α$ ，则A ， C两处相距为（）

A、 $\frac{x}{s i n α}$ 米 B、 $\frac{x}{c o s α}$ 米 C、 $x \cdot s i n α$ 米 D、 $x \cdot c o s α$ 米

查看试题解析
6. 如图，下列条件不能判定 $△ B D C ∽ △ A B C$ 的是（）

A、 $∠ B D C = ∠ A B C$ B、 $∠ D B C = ∠ B A C$ C、 $B C^{2} = D C \cdot A C$ D、 $\frac{A D}{A B} = \frac{A B}{B C}$

查看试题解析
7. 在 $△ A B C$ 中， $∠ C = 90 °, A C = B C$ ，则 $s i n A$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、1

查看试题解析
8. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $B C = 3$ ， $A C = \sqrt{3}$ ，则 $∠ A$ 的度数是（）

A、 $30 °$ B、 $40 °$ C、 $45 °$ D、 $60 °$

查看试题解析
9. 已知反比例函数 $y = - \frac{4}{x}$ ，则下列描述正确的是（）

A、图象位于第一、三象限 B、y随x的增大而增大 C、图象不可能与坐标轴相交 D、图象必经过点 $(\frac{3}{2}, \frac{8}{3})$

查看试题解析
10. 如图，小树AB在路灯O的照射下形成投影BC．若树高AB=2m，树影BC=3m，树与路灯的水平距离BP=4.5m．则路灯的高度OP为（）

A、3m B、4m C、4.5m D、5m

查看试题解析
11. 一次函数 $y = - a x - a$ 与反比例函数 $y = \frac{a}{x}$ 在同一平面直角坐标系中的图象可能是（）

A、 B、 C、 D、

查看试题解析
12. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C = 4, C D ⊥ A B$ 于点D ， P是 $A B$ 上的一个动点，以点P为直角顶点向右作等腰 $R t △ C P E$ ，连接 $D E$ ，则 $D E$ 的最小值为（）

A、1 B、 $\sqrt{2}$ C、2 D、 $2 \sqrt{2} - 1$

查看试题解析

二、填空题（本大题共6小题，每小题2分，共12分．）

13. 主视图、左视图和俯视图完全相同的几何体是（写出一种即可）．

查看试题解析
14. 已知一个小球由地面沿着坡度为 $i = 1 : 2$ 的坡面向上前进 $10 c m$ ，则此时小球距离地面的高度为 $c m$ ．

查看试题解析
15. 如图， $A B ∥ C D ∥ E F, A C = 3, C E = 5, B D = 2$ ，则 $B F$ 的长是．

查看试题解析
16. 某电路中，电源的电压为定值，电流 $I (A)$ 与电阻 $R (Ω)$ 成反比例，如图表示的是该电路中电流I与电阻R之间关系的图象，则用R表示I的函数解析式为．

查看试题解析
17. 如果 $△ A B C ∽ △ D E F$ ，且 $△ A B C$ 的三边长分别为3，5，6， $△ D E F$ 的最短边长为9，那么 $△ D E F$ 的周长为．

查看试题解析
18. 如图，点A ， B在反比例函数 $y = \frac{1}{x} (x > 0)$ 的图象上，点C ， D在反比例函数 $y = \frac{k}{x} (k > 0, x > 0)$ 的图象上， $A C ∥ B D ∥ y$ 轴，已知点A ， B的横坐标分别为2，4， $△ O A C$ 与 $△ A B D$ 的面积之差为1，则k的值为．

查看试题解析

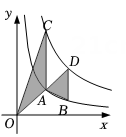
三、解答题（本大题共8小题，共72分，解答应写出文字说明、证明过程或演算步骤．）

19. 计算：

(1)、 $s i n^{2} 60 ° + c o s^{2} 60 °$ ；

(2)、 $c o s 45 ° + t a n 60 ° c o s 30 °$ ．

查看试题解析
20. 如图，在Rt△ABC中，∠C＝90°，BC＝2，AC＝2 $\sqrt{3}$ ．解这个直角三角形．

查看试题解析
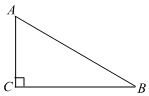21. 如图，在平面直角坐标系中， $△ A B C$ 各顶点的坐标为 $A (- 1, 1)$ ， $B (2, 3), C (0, 3)$ ．

(1)、以坐标原点O为位似中心，在x轴上方作与 $△ A B C$ 的位似比为2的位似图形 $△ A^{'} B^{'} C^{'}$ ．

(2)、顶点 $A^{'}$ 的坐标为， $△ A^{'} B^{'} C^{'}$ 与 $△ A B C$ 的面积之比为．

查看试题解析
22. 一个几何体的三视图如图所示．

(1)、写出这个几何体的名称；

(2)、求这个几何体侧面展开图的圆心角；

(3)、求这个几何体的全面积（结果保留π）．

查看试题解析
23. 已知反比例函数 $y = \frac{k + 1}{x}$ ．

(1)、若该函数的图象经过点 $A (2, - 2)$ ，求k的值，并在平面直角坐标系中画出该函数的大致图象；

(2)、当 $x > 0$ 时，y随x的增大而减小，求k的取值范围．

查看试题解析
24. 如图，在 $△ A B C$ 中， $∠ B A C = 90 °$ ， M是斜边 $B C$ 的中点， $B N ⊥ A M$ ，垂足为点N ，且 $B N$ 的延长线交 $A C$ 于点D．

(1)、求证 $△ A B C ∽ △ A D B$ ；

(2)、如果 $B C = 20, B D = 15$ ，求 $A B$ 的长度．

查看试题解析
25. 百惠超市从果农处购进柚子的成本价为3元/千克，在销售过程中发现，每天的销售量y（千克）与销售单价x（元/千克）之间的关系如图所示，其中 $A B$ 为反比例函数图象的一部分， $B C$ 为一次函数图象的一部分．

(1)、求y与x的函数关系式；

(2)、当销售单价为多少元时，该超市每天的销售利润最大？最大利润是多少元？

查看试题解析
26. 综合与实践．
李老师善于通过合适的主题整合教学内容，帮助同学们用整体的、联系的、发展的眼光看问题，形成科学的思维习惯．下面是李老师在“相似”主题下设计的问题，请你解答．
【问题情境】
在 $△ A B C$ 中， $A B = A C, D$ 是 $B C$ 边上一点， $∠ A D E = ∠ B, D E$ 与 $A C$ 交于点E ．
【初步探究】
图1 图2

(1)、如图1，若 $D E ∥ A B, E F ⊥ A D$ 于点F ．
①求证 $A B^{2} = B D \cdot B C$ ；
②求 $\frac{D F}{C D}$ 的值．

(2)、【拓展延伸】
如图2，G是 $D E$ 延长线上一点，若 $G A ⊥ A D, G D = G C$ ，已知 $A B = 10, B C = 16$ ，求 $B D$ 的长．

查看试题解析