湖南省长沙市重点中学2023-2024学年八年级下学期开学考试数学试题

试卷更新日期：2024-04-08 类型：开学考试

进入出卷网下载

一、单选题（共10小题，每小题2分．共20分）

1. 现实世界中，对称现象无处不在，中国的方块字中有些也具有对称性，下列美术字是轴对称图形的是（）

A、诚 B、信 C、友 D、善

查看试题解析
2. 要使分式 $\frac{x}{x - 2}$ 有意义，则 $x$ 的取值应满足（）

A、 $x \neq 2$ B、 $x \neq - 2$ C、 $x = 2$ D、 $x = - 2$

查看试题解析
3. 下列计算正确的是（）

A、 $b^{3} \cdot b^{3} = 2 b^{3}$ B、 ${(a b^{2})}^{3} = a^{3} b^{6}$ C、 $a^{10} \div a^{2} = a^{5}$ D、 $a^{2} + a^{3} = a^{5}$

查看试题解析
4. 化简 $\sqrt{54} \times \sqrt{\frac{1}{2}} + \sqrt{12}$ 的结果是( ).

A、 $5 \sqrt{2}$ B、 $6 \sqrt{3}$ C、 $\sqrt{3}$ D、 $5 \sqrt{3}$

查看试题解析
5. 下列各组数中，以它们为边长能构成直角三角形的是（）

A、1，3，3 B、2，3，4 C、6，8，9 D、5，12，13

查看试题解析
6. 已知： $(2 x + 1) (x - 3) = 2 x^{2} + p x + q$ ，则p ， q的值分别为（）

A、5，3 B、5，－3 C、－5，3 D、－5，－3

查看试题解析
7. 若 $(a + b)^{2} = 49$ ， $a b = 12$ ，则 $a^{2} + b^{2}$ 的值为（）

A、 $20$ B、 $25$ C、 $30$ D、 $35$

查看试题解析
8. 某工厂计划x天内生产120件零件，由于采用新技术，每天增加生产3件，因此提前2天完成计划，列方程为（）

A、 $\frac{120}{x} = \frac{120}{x - 2} + 3$ B、 $\frac{120}{x - 2} = \frac{120}{x} + 3$ C、 $\frac{120}{x + 2} = \frac{120}{x} + 3$ D、 $\frac{120}{x} = \frac{120}{x + 2} + 3$

查看试题解析
9. 若 $\frac{a}{2} = \frac{b}{3} \neq 0$ ，则 $\frac{a + b}{a - 2 b}$ 的值是（）

A、 $\frac{4}{5}$ B、 $- \frac{4}{5}$ C、 $\frac{5}{4}$ D、 $- \frac{5}{4}$

查看试题解析
10. 如图，已知在等边 $△ A B C$ 中， $A D ⊥ B C$ ， $A B = 8 \sqrt{3}$ ，若点P在线段AD上运动，当 $\frac{1}{2} A P + B P$ 有最小值时，最小值为（）

A、 $4 \sqrt{3}$ B、 $8 \sqrt{3}$ C、10 D、12

查看试题解析

二、填空题（共6小题，每小题3分，共18分）

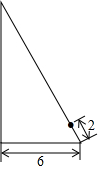
11. 点A（－3，2）关于 $y$ 轴对称的点的坐标是．

查看试题解析
12. 数0.0000046用科学记数法表示为：．

查看试题解析
13. 分解因式：mn²+6mn+9m= ．

查看试题解析
14. 若y $= \sqrt{x - 2} + \sqrt{2 - x} + \sqrt{3}$ ，则xy＝．

查看试题解析
15. 如图，小明想知道学校旗杆的高度，他将升旗的绳子拉到旗杆底端，并在绳子上打了一个结，然后将绳子拉到离旗杆底端 $6 m$ 处，发现此时绳子底端距离打结处 $2 m$ ，则旗杆的高度为 $m .$

查看试题解析
16. 如果关于x的方程 $\frac{2 x + m}{x - 1} = 1$ 的解是正数，那么m的取值范围是．

查看试题解析

三、解答题（共9小题．17、18、19每题6分，20、21每题8分，22、23每题9分，24，25每题10分，共72分）

17. 计算： ${(- \frac{1}{3})}^{- 2} - (π - 5)^{0} - \sqrt{8} + | - 2 \sqrt{2} |$ ．

查看试题解析
18. 先化简．再求值： $(a + b) (a - b) + {(a + b)}^{2}$ ，其中 $a = - 1 ， b = \frac{1}{2}$

查看试题解析
19. 解方程： $\frac{x}{x - 3} - \frac{1}{x + 3} = 1$ ．

查看试题解析
20. 某校为了解疫情期间学生在家上网课的学习情况，随机抽取了该校部分学生对其学习效果进行调查，根据相关数据，绘制成如图不完整的统计图．

(1)、此次调查的样本容量为，学习效果“较差”的部分对应的圆心角度数为；

(2)、补全条形图；

(3)、请估计该校3000名学生疫情期间网课学习效果“一般”的学生人数．

查看试题解析
21. 如图．在△ABC中，AB＝AC ， ∠BAC＝90°，AE是过点A的一直线，且B ， C在AE的两侧，BD⊥AE于D ， CE⊥AE于E ．

(1)、求证： $△ A B D ≌ △ C A E$

(2)、若DE＝3，CE＝2，求BD ．

查看试题解析
22. 某公司计划购买A，B两种型号的机器人搬运材料．已知A型机器人比B型机器人每小时多搬运30kg材料，且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同．

(1)、求A，B两种型号的机器人每小时分别搬运多少材料；

(2)、该公司计划采购A，B两种型号的机器人共20台，要求每小时搬运材料不得少于2800kg，则至少购进A型机器人多少台？

查看试题解析
23. 在△ABC中，∠B＝∠C ，点D在边AB上，过点D作DE⊥BC于点E ．

(1)、如图1，求证： $∠ A = 2 ∠ B D E$ ；

(2)、如图2，点F在AC边上，连接EF ，使∠FED＝∠B ，若 $2 ∠ F D E + ∠ B = 180 °$ ，求证： $B C = B D + C F$ ；

(3)、如图3，在（2）的条件下，过点D作 $D G ⊥ D E$ ，交边AC于G ，点G是AF中点，求证：△ADG是等边三角形．

查看试题解析
24. 若三个非零实数x、y、z满足：若其中一个数的倒数等于另外两个数的倒数的和，则称这三个实数x、y、z构成“和谐三数组”。例如：因为 $\frac{1}{2}$ 、 $\frac{1}{5}$ 、 $\frac{1}{3}$ 的倒数能够满足 $2 + 3 = 5$ ，所以数组－ $\frac{1}{2}$ 、 $\frac{1}{5}$ 、 $\frac{1}{3}$ 构成“和谐三数组”

(1)、下列三组数构成“和谐三数组”的有；（填序号）
①1、2、3；②1、 $\frac{1}{2}$ 、 $\frac{1}{3}$ ；③ $\sqrt{3} + 1$ 、 $\frac{\sqrt{3}}{3}$ 、 $\sqrt{3} - 1$ ．

(2)、若 $\frac{k}{t}$ 、 $\frac{k}{t + 1}$ 、 $\frac{k}{t + 2} (k \neq 0)$ 构成“和谐三数组”，求实数 $t$ 的值；

(3)、若非零实数 $\frac{c}{a}$ 、 $\frac{c}{b}$ 、 $- 1$ 构成“和谐三数组”，且满足以下三个条件：① $a + b + c = 0$ ；②点 $P (\frac{c}{a} ， \frac{b}{a})$ 到原点的距离记为 $n$ ；③不等式 $\frac{3 m - 6}{m + 1} + \frac{1}{2} < n^{2}$ 恒成立。求实数 $m$ 的取值范围．

查看试题解析
25. 如图，在△ABC中， $∠ A C B = 90 °$ ， AB＝5，BC＝3，若动点P从点A出发，以1个单位每秒的速度沿折线 $A - C - B - A$ 运动，设运动时间为t秒．

(1)、若点P在AC上，且满足PA＝PB ，求出此时 $t$ 的值；

(2)、若点P恰好在∠BAC的平分线上，求 $t$ 的值；

(3)、在运动过程中，直接写出当 $t$ 为何值时，△BCP为等腰三角形．

查看试题解析