广西钦州市浦北县2023-2024学年七年级下学期3月月考数学试题

试卷更新日期：2024-04-08 类型：月考试卷

进入出卷网下载

一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中只有一项是符合要求的，请用2B铅笔把答题卡上对应题目的答案标号涂黑．）

1. 下列选项中，是无理数的是（　　）

A、 $\sqrt{4}$ B、3.14 C、 $\sqrt[3]{2}$ D、 $\frac{2}{7}$

查看试题解析
2. 体育课上老师按照如图所示的方式测量同学的跳远成绩，这里面蕴含的数学原理是（）

A、垂线段最短 B、两点之间，线段最短 C、平面内，过一点有且只有一条直线与已知直线垂直 D、两点确定一条直线

查看试题解析
3.
如图，直线a，b被直线c所截，则下列说法中错误的是（　　）

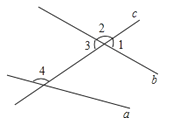A、∠1与∠2是邻补角 B、∠1与∠3是对顶角 C、∠2与∠4是同位角 D、∠3与∠4是内错角

查看试题解析
4. 下列说法正确的是（）

A、4的算术平方根是2 B、0.16的平方根是0.4 C、0没有立方根 D、1的立方根是±1

查看试题解析
5. 下列各式计算正确的是（）

A、 $\sqrt{36} = \pm 6$ B、 $\pm \sqrt{16} = \pm 4$ C、 $\sqrt{(- 5)^{2}} = - 5$ D、 $\sqrt{- 100} = 10$

查看试题解析
6. 如图，直线 $A B$ 、 $C D$ 相交于点O， $∠ A O E = 2 ∠ A O C$ ，若 $∠ 1 = 38 °$ ，则 $∠ D O E$ 等于（）

A、 $66 °$ B、 $76 °$ C、 $90 °$ D、 $144 °$

查看试题解析
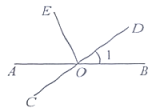7. 如图，下列条件中不能判定 $A B ∥ C D$ 的是（）

A、 $∠ 3 = ∠ 4$ B、 $∠ 3 = ∠ 5$ C、 $∠ 1 + ∠ 4 = 180 °$ D、 $∠ 1 = ∠ 5$

查看试题解析
8. 如图， $△ A B C$ 向右平移2cm得到 $△ D E F$ ，如果四边形 $A B F D$ 的周长是20cm，那么 $△ A B C$ 的周长是（）

A、14cm B、16cm C、18cm D、20cm

查看试题解析
9. 如图，数轴上的点A可以用实数a表示，下面式子成立的是（）

A、 $| a | > 1$ B、 $| a - 1 | = 1 - a$ C、 $a + 1 < 0$ D、 $- \frac{1}{a} < 1$

查看试题解析
10. 已知 $\sqrt[3]{7} = a$ ，则 $\sqrt[3]{0.007} + \sqrt[3]{7000}$ 的值是（）

A、 $0.1 a$ B、 $a$ C、 $1.1 a$ D、 $10.1 a$

查看试题解析
11. 如图a是长方形纸带，∠DEF=26°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数是（）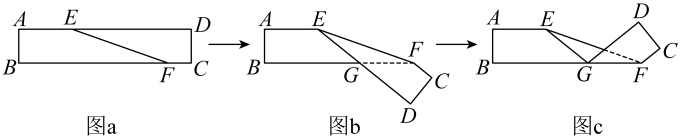

A、102° B、108° C、124° D、128°

查看试题解析
12. 十六世纪，意大利数学家塔尔塔利亚把大正方形分割成11个小正方形．若图中所给的三个小正方形的面积分别为4，9和16，则这个大正方形的边长为（）

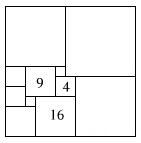A、11 B、12 C、13 D、14

查看试题解析

二、填空题（本大题共6小题，每小题2分，共12分．）

13. 一个数的平方根等于它本身，则这个数是．

查看试题解析
14. 比较大小 $\sqrt{5}$ $\sqrt{6}$ （填“ $>$ ”、“ $<$ ”或“ $=$ ”）．

查看试题解析
15. 将命题“对顶角相等”改写成“如果……，那么……”的形式：.

查看试题解析
16. 从A沿北偏东60°的方向行驶到B ，再从B沿南偏西20°方向行驶到 $C$ ，则 $∠ A B C =$ 度．

查看试题解析
17. 如图，二阶魔方为 $2 \times 2 \times 2$ 的正方体结构，本身只有8个方块，没有其他结构的方块，已知二阶魔方的体积约为 $72 c m^{3}$ （方块之间的缝隙忽略不计），那么每个方块的棱长为 $c m$ ．

查看试题解析
18. 如图，直线 $A B ∥ C D$ ，点 $E$ 在 $A B$ 上，点 $F$ 在 $C D$ 上，点 $P$ 在 $A B, C D$ 之间， $∠ A E P$ 和 $∠ C F P$ 的角平分线相交于点 $M, ∠ D F P$ 的角平分线交 $E M$ 的反向延长线于点 $N$ ，下列四个结论：
① $∠ E P F = ∠ A E P + ∠ C F P$ ；
② $∠ E P F = 2 ∠ M$ ；
③若 $E P ∥ F N$ ，则 $∠ A E M = ∠ C F M$ ；
④ $∠ M N F + ∠ P E M = 90 ° - ∠ P F M$ ．
其中正确的结论是（填写序号）．

查看试题解析

三、解答题（本大题共8小题，共72分．解答应写出文字说明、证明过程或演算步骤．）

19. 计算：

(1)、 $\sqrt[3]{8} + \sqrt{0} - \sqrt{\frac{1}{4}}$

(2)、 $5 \sqrt{3} - 6 \sqrt{3} + | 1 - \sqrt{3} |$

查看试题解析
20. 求下列各式中x的值.

(1)、 ${(x - 4)}^{2} = 9$ ；

(2)、 $27 x^{3} + 8 ＝ 0$ .

查看试题解析
21. 如图，直线 $A B$ ， $C D$ 相交于点 $O$ ， $E O ⊥ A B$ ，垂足为 $O$ .

(1)、若 $∠ E O C = 35 °$ ，求 $∠ A O D$ 的度数；

(2)、若 $∠ B O C = 2 ∠ A O C$ ，求 $∠ D O E$ 的度数.

查看试题解析
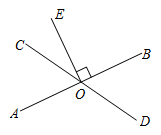22. 勤俭节约是中国人民的传统美德，涛涛的爷爷是能工巧匠，他先做了一张边长为 $13 d m$ 的正方形桌子，结果涛涛说桌子太大，想让爷爷做成面积为 $144 d m^{2}$ 的桌子，于是爷爷在原有桌子的基础上，在两边等距消去宽为 $x$ 的阴影部分，于是空白部分成为了涛涛想要的为 $144 d m^{2}$ 的桌子，请问 $x$ 的长度为多少？

查看试题解析
23. 如图，在边长为1个单位长度的小正方形组成的网格中．

(1)、把三角形 $A B C$ 平移至 $A^{'}$ 的位置，使点 $A$ 与 $A^{'}$ 对应，得到三角形 $A^{'} B^{'} C^{'}$ ；

(2)、连接 $A A^{^{'}}, B B^{^{'}}$ ，线段 $A A^{'}$ 与 $B B^{'}$ 的位置及数量关系是；

(3)、求三角形 $A B C$ 的面积．

查看试题解析
24. 已知某正数的平方根分别是2a-7和a+4，b-7的立方根为-2．

(1)、求a，b的值；

(2)、求a+b的算术平方根．

查看试题解析
25. 如图，已知 $∠ 1 = ∠ 2$ ， $∠ 3 = ∠ 4$ ， $∠ 5 = ∠ A$ ，试说明： $B E ∥ C F$ ．
完善下面的解答过程，并填写理由或数学式：解：
∵ $∠ 3 = ∠ 4$ （已知）
∴ $A E ∥$ _▲_（_▲_）
∴ $∠ E D C = ∠ 5$ （_▲_）
∵ $∠ 5 = ∠ A$ （已知）
∴ $∠ E D C =$ _▲_（等量代换）
∴ $D C ∥ A B$ （_▲_）
∴ $∠ 5 + ∠ A B C = 180 °$ （_▲_）
即 $∠ 5 + ∠ 2 + ∠ 3 = 180 °$
∵ $∠ 1 = ∠ 2$ （已知）
∴ $∠ 5 + ∠ 1 + ∠ 3 = 180 °$ （_▲_）
即 $∠ B C F + ∠ 3 = 180 °$
∴ $B E ∥ C F$ （_▲_）．

查看试题解析
26. 综合实践．
我们发现平行线具有“等角转化”的功能，通过添加平行线可将不同位置的角“凑”在一起，得出角之间的关系．根据平行线的“等角转化”功能，解答下列问题：

(1)、阅读理解：如图1， $A P, C P$ 相交于点 $P$ ，请说明 $∠ A P C = ∠ A + ∠ C$ ．阅读并补充下面推理过程．

解：如图1，过点 $P$ 作 $P Q ∥ A B$ ．
$∴ ∠ A =$ _▲_．
$∵ A B ∥ C D$ ，
$∴$ _▲_．
$∴ ∠ C =$ _▲_．
$∴ ∠ A P Q + ∠ C P Q = ∠ A + ∠ C$ ．
即 $∠ A P C = ∠ A + ∠ C$ ．

(2)、方法掌握：如图2，已知 $∴ A B ∥ C D, A M, C M$ 交于点 $M$ ．请写出 $∠ A, ∠ A M C, ∠ C$ 之间的数量关系，并证明你的结论；

(3)、拓展运用：如图3，已知 $A B ∥ C D$ ，点 $P$ 在直线 $A B$ 上， $C E$ 平分 $∠ P C D, D E$ 平分 $∠ P D C$ ．若 $∠ C P D = n °$ ，求 $∠ C E D$ 度数（用含 $n$ 的式子表示）．

查看试题解析