广西北部湾经济区2024年中考数学模拟试卷(4月份)
试卷更新日期:2024-04-08 类型:中考模拟
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 的相反数是( )A、 B、 C、 D、2. 在下列现象中,属于平移的是( )A、小亮荡秋千运动 B、升降电梯由一楼升到八楼
C、时针的运行过程 D、卫星绕地球运动3. 下列说法不正确的是( )A、为了审核书稿中的错别字,选择普查
B、为了解春节联欢晚会的收视率,选择抽样调查
C、为了清楚地反映事物的变化情况,可选用扇形统计图
D、频数与总次数的比值是频率4. 下列命题是真命题的有个.( )
直线外一点到这条直线的垂线段叫做点到直线的距离;
过一点有且只有一条直线与已知直线垂直;
过一点有且只有一条直线与已知直线平行;
有理数与数轴上的点一一对应;
圆周率是一个无理数.A、 B、 C、 D、5. 如图,数轴上表示的解集是下列哪个不等式的解集( ) A、 B、 C、 D、6. 如图,于 , , 若 , 则等于( )
A、 B、 C、 D、6. 如图,于 , , 若 , 则等于( ) A、 B、 C、 D、7. 下列说法中,正确的是( )A、一组数据 , , , , , 的中位数是
A、 B、 C、 D、7. 下列说法中,正确的是( )A、一组数据 , , , , , 的中位数是
B、质检部门要了解一批灯泡的使用寿命,应当采用普查的调查方式
C、购买一张福利彩票中奖是一个确定事件
D、分别写有三个数字 , , 的三张卡片卡片的大小形状都相同 , 从中任意抽取两张,则卡片上的两数之积为正数的概率为8. 如图,市政府准备修建一座高的过街天桥,已知天桥的坡面与地面的夹角的余弦值为 , 则坡面的长度为( ) A、 B、 C、 D、9. 下列计算正确的是( )A、 B、 C、 D、10. 甲、乙两人加工某种机械零件,已知甲每小时比乙多加工个,甲加工个所用的时间与乙加工个所用的时间相等设甲每小时加工个零件,则可列方程为( )A、 B、 C、 D、11. 如图,点A在反比例函数第一象限内的图象上,点B在x轴的正半轴上,OA=AB,△AOB的面积为2,则a的值为( )
A、 B、 C、 D、9. 下列计算正确的是( )A、 B、 C、 D、10. 甲、乙两人加工某种机械零件,已知甲每小时比乙多加工个,甲加工个所用的时间与乙加工个所用的时间相等设甲每小时加工个零件,则可列方程为( )A、 B、 C、 D、11. 如图,点A在反比例函数第一象限内的图象上,点B在x轴的正半轴上,OA=AB,△AOB的面积为2,则a的值为( )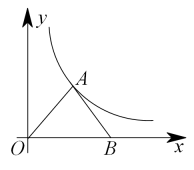 A、 B、 C、2 D、112. 在平面直角坐标系中,函数与的图象大致是( )A、
A、 B、 C、2 D、112. 在平面直角坐标系中,函数与的图象大致是( )A、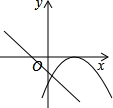 B、
B、
C、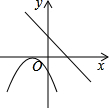 D、
D、
二、填空题:本题共6小题,每小题3分,共18分。
-
13. .14. 若分式的值为 , 则 .15. 掷一个骰子,观察向上的面的点数,则点数为奇数的概率为 .16. 如图是小孔成像原理的示意图,根据图中所标注的尺寸,蜡烛在暗盒中所成的像的高度是 .
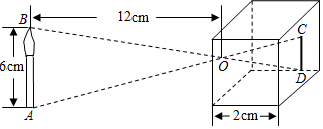 17. 已知a、b、c都是实数,若 , 则 .18. 直线常数和双曲线的图象有且只有一个交点 , 一次函数与轴交于点 , 点是线段上的动点,点在反比例函数图象上,且满足设与线段的交点为 , 若 , 则的值为 .
17. 已知a、b、c都是实数,若 , 则 .18. 直线常数和双曲线的图象有且只有一个交点 , 一次函数与轴交于点 , 点是线段上的动点,点在反比例函数图象上,且满足设与线段的交点为 , 若 , 则的值为 .
三、计算题:本大题共2小题,共12分。
-
19. 计算:20. 计算:
(1)、;(2)、;(3)、 .四、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
-
21. 有一个平分角的仪器如图所示,其中AB=AD,BC=DC.求证:AC平分∠BAD.
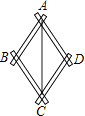 22. 为了了解秦兵马俑的身高状况,某考古队随机调查了尊秦兵马俑,它们的高度单位:如下:
22. 为了了解秦兵马俑的身高状况,某考古队随机调查了尊秦兵马俑,它们的高度单位:如下:
, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , .
(1)、这尊秦兵马俑高度的平均数、中位数和众数分别是多少?(2)、你能据此估计出秦兵马俑的平均高度吗?23. 有这样一个问题:探究函数的图象与性质一位同学根据学习函数的经验,对函数的图象与性质进行了探究.
(1)、下面是这位同学的探究过程,请补充完整:
函数的自变量的取值范围是_▲_;
如表是与的几组对应值,则的值是_▲_;如图,在平面直角坐标系中,描出以补全后的表中各对对应值为坐标的点,并画出该函数的图象:
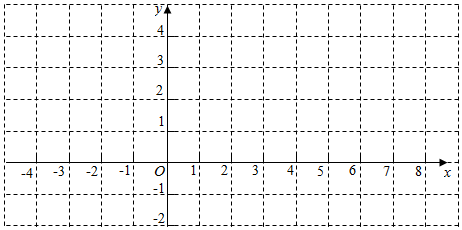
观察此函数图象,写出一个正确的函数性质或者函数图象性质:_▲_.(2)、直接写出:当 时, .24. 如图,在中, , 以为直径的半圆交于点 , 过点作交于点 , 连结 , .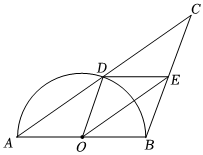 (1)、求证:;(2)、填空:
(1)、求证:;(2)、填空:
当 时,四边形是菱形;
当 时,四边形的面积最大.25. 综合与探究
如图,已知抛物线与轴交于 , 两点点位于点的右边 , 与轴交于点 , 连接 , 是抛物线上的一动点,点的横坐标为 .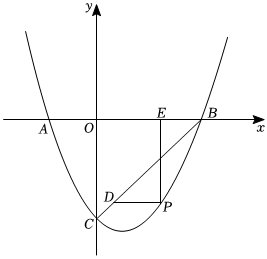 (1)、求 , 两点的坐标.(2)、若 , 点位于第四象限,过点作轴的平行线交于点 , 过点作轴的平行线交轴于点 , 求的最大值及此时点的坐标.(3)、在中取得最大值的条件下,将该抛物线沿水平方向向左平移个单位长度,为点的对应点,平移后的抛物线与轴交于点 , 为平移后的抛物线的对称轴上一点在平移后的抛物线上确定一点 , 使得以 , , , 为顶点的四边形是平行四边形,直接写出所有符合条件的点的坐标.26. 如图,在▱中,点是对角线的中点,点在上,且 , 连接并延长交于点过点作的垂线,垂足为 , 交于点 .
(1)、求 , 两点的坐标.(2)、若 , 点位于第四象限,过点作轴的平行线交于点 , 过点作轴的平行线交轴于点 , 求的最大值及此时点的坐标.(3)、在中取得最大值的条件下,将该抛物线沿水平方向向左平移个单位长度,为点的对应点,平移后的抛物线与轴交于点 , 为平移后的抛物线的对称轴上一点在平移后的抛物线上确定一点 , 使得以 , , , 为顶点的四边形是平行四边形,直接写出所有符合条件的点的坐标.26. 如图,在▱中,点是对角线的中点,点在上,且 , 连接并延长交于点过点作的垂线,垂足为 , 交于点 . (1)、求证:;(2)、若 .
(1)、求证:;(2)、若 .
求证:;
探索与的数量关系,并说明理由.