广西壮族自治区南宁天桃教育集团2023-2024学年九年级下学期第二次月考数学试题
试卷更新日期:2024-04-08 类型:月考试卷
一、选择题(本大题共12小题,每小题3分,共36分.每小题给出的四个选项中只有一项是符合要求的,用2B铅笔把答题卡上对应题目的答案标号涂黑.)
-
1. -2的倒数是( )A、2 B、 C、 D、-22. 我国古代典籍《周易》用“卦”描述万物的变化.下图为部分“卦”的符号,其中是中心对称图形的是( )A、
 B、
B、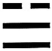 C、
C、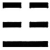 D、
D、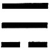 3. 今年春节电影《热辣滚烫》《飞驰人生2》《熊出没逆转时空》《第二十条》在网络上持续引发热议,据国家电影局2月18日发布数据,我国2024年春节档电影票房达8016000000元,创造了新的春节档票房纪录.其中数据8016000000用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、3a2﹣a23 B、(a2)3a6 C、a2•a3a6 D、a6÷a2a35. 以下调查中,最适合用来全面调查的是( )A、调查邕江流域水质情况 B、了解全国中学生的心理健康状况 C、了解全班学生的身高情况 D、调查春节联欢晚会收视率6. 使二次根式有意义的x的取值范围是( )A、x≥1 B、x>1 C、x≠1 D、x<17. 已知圆锥的母线长为10,侧面展开图面积为60π,则该圆锥的底面圆的半径长等于( )A、4 B、6 C、8 D、128. 某学校开设了劳动教育课程.小韦从感兴趣的“种植”“烹饪”“陶艺”“木工”4门课程中随机选择一门学习,每门课程被选中的可能性相等.小韦恰好选中“烹饪”的概率为( )A、 B、 C、 D、9. 2024年春节联欢晚会为海内外受众奉上了一道心意满满、暖意融融的除夕“文化大餐”.截至2月10日2时,总台春晚中“竖屏看春晚”直播播放量4.2亿次.据统计,2022年首次推出的“竖屏看春晚”累计观看2亿次,设“竖屏看春晚”次数的年平均增长率为 , 则可列出关于的方程( )A、 B、 C、 D、10. 如图, , 点和点是对应顶点,点和点是对应顶点,过点作 , 垂足为点 , 若 , 则的度数为( )
3. 今年春节电影《热辣滚烫》《飞驰人生2》《熊出没逆转时空》《第二十条》在网络上持续引发热议,据国家电影局2月18日发布数据,我国2024年春节档电影票房达8016000000元,创造了新的春节档票房纪录.其中数据8016000000用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、3a2﹣a23 B、(a2)3a6 C、a2•a3a6 D、a6÷a2a35. 以下调查中,最适合用来全面调查的是( )A、调查邕江流域水质情况 B、了解全国中学生的心理健康状况 C、了解全班学生的身高情况 D、调查春节联欢晚会收视率6. 使二次根式有意义的x的取值范围是( )A、x≥1 B、x>1 C、x≠1 D、x<17. 已知圆锥的母线长为10,侧面展开图面积为60π,则该圆锥的底面圆的半径长等于( )A、4 B、6 C、8 D、128. 某学校开设了劳动教育课程.小韦从感兴趣的“种植”“烹饪”“陶艺”“木工”4门课程中随机选择一门学习,每门课程被选中的可能性相等.小韦恰好选中“烹饪”的概率为( )A、 B、 C、 D、9. 2024年春节联欢晚会为海内外受众奉上了一道心意满满、暖意融融的除夕“文化大餐”.截至2月10日2时,总台春晚中“竖屏看春晚”直播播放量4.2亿次.据统计,2022年首次推出的“竖屏看春晚”累计观看2亿次,设“竖屏看春晚”次数的年平均增长率为 , 则可列出关于的方程( )A、 B、 C、 D、10. 如图, , 点和点是对应顶点,点和点是对应顶点,过点作 , 垂足为点 , 若 , 则的度数为( ) A、 B、 C、 D、11. 若点在抛物线上,则下列各点在抛物线上的是( )A、 B、 C、 D、12. 如图,已知点A是一次函数的图象上一点,过点A作x轴的垂线l , B是l上一点(B在A上方),在的右侧以为斜边作等腰直角三角形 , 反比例函数的图象过点B , C , 若的面积为16,则的面积是( )
A、 B、 C、 D、11. 若点在抛物线上,则下列各点在抛物线上的是( )A、 B、 C、 D、12. 如图,已知点A是一次函数的图象上一点,过点A作x轴的垂线l , B是l上一点(B在A上方),在的右侧以为斜边作等腰直角三角形 , 反比例函数的图象过点B , C , 若的面积为16,则的面积是( ) A、3 B、4 C、6 D、12
A、3 B、4 C、6 D、12二、填空题(本大题共6小题,每小题2分,共12分.)
-
13. 单项式-3ab的系数是 .14. 分解因式:a2-36= .15. 如图,在RtABC中, , , 则为 .
 16. 若正多边形的一个中心角为60°,则这个正多边形的一个内角等于°.17. 如图,矩形中, , , 将矩形沿对角线对折,的对应边与相交于点 , 则的长为 .
16. 若正多边形的一个中心角为60°,则这个正多边形的一个内角等于°.17. 如图,矩形中, , , 将矩形沿对角线对折,的对应边与相交于点 , 则的长为 . 18. 如图,等边三角形的边长为 , 动点从点出发以的速度沿向点匀速运动,过点作 , 交边于点 , 以为边作等边三角形 , 使点 , 在异侧,当点落在边上时,点需移动 .
18. 如图,等边三角形的边长为 , 动点从点出发以的速度沿向点匀速运动,过点作 , 交边于点 , 以为边作等边三角形 , 使点 , 在异侧,当点落在边上时,点需移动 .
三、解答题(本大题共8小题,共72分.解答应写出文字说明、证明过程或演算步骤.)
-
19. 计算:.20. 解不等式组: , 并用数轴确定不等式组的解集.
 21. 如图,已知中,为的中点.
21. 如图,已知中,为的中点. (1)、请用尺规作边的垂直平分线,交AC于点 , 交BC于点F,并连接(保留作图痕迹,不要求写作法).(2)、在(1)的条件下,若的周长为3,求的周长 .22. 为了解中学生的视力情况,某区卫健部门决定随机抽取本区部分初、高中学生进行调查,并对他们的视力数据进行整理,得到如下统计表和统计图.
(1)、请用尺规作边的垂直平分线,交AC于点 , 交BC于点F,并连接(保留作图痕迹,不要求写作法).(2)、在(1)的条件下,若的周长为3,求的周长 .22. 为了解中学生的视力情况,某区卫健部门决定随机抽取本区部分初、高中学生进行调查,并对他们的视力数据进行整理,得到如下统计表和统计图.初中学生视力情况统计表
视力
人数
百分比
0.6及以下
8
0.7
16
0.8
28
0.9
34
1.0
1.1及以上
46
合计
200
 (1)、 , ;(2)、被调查的高中学生视力情况的样本容量为;(3)、约定:视力达到1.0及以上视为视力良好.若该区有10000名中学生,估计该区有多少名中学生视力良好?并对视力保护提出一条合理化建议.23. 如图,在中, , , 以为直径的与相交于点 , 为上一点,且 .
(1)、 , ;(2)、被调查的高中学生视力情况的样本容量为;(3)、约定:视力达到1.0及以上视为视力良好.若该区有10000名中学生,估计该区有多少名中学生视力良好?并对视力保护提出一条合理化建议.23. 如图,在中, , , 以为直径的与相交于点 , 为上一点,且 . (1)、求的长;(2)、若 , 求证:为的切线.24. 为提升学生身体素质,落实教育部门“在校学生每天锻炼时间不少于1小时”的文件精神.某校利用课后服务时间,在九年级开展“体育赋能,助力成长”班级篮球赛,共13个班级参加.(1)、比赛积分规定:每场比赛都要分出胜负,胜一场积3分,负一场积1分.某班级在12场比赛中获得总积分为32分,问该班级胜负场数分别是多少?(2)、投篮得分规则:在3分线外投篮,投中一球可得3分,在3分线内(含3分线)投篮,投中一球可得2分,某班级在其中一场比赛中,共投中22个球(只有2分球和3分球),所得总分不少于50分,问该班级这场比赛中至少投中了多少个3分球?25. 综合与实践:
(1)、求的长;(2)、若 , 求证:为的切线.24. 为提升学生身体素质,落实教育部门“在校学生每天锻炼时间不少于1小时”的文件精神.某校利用课后服务时间,在九年级开展“体育赋能,助力成长”班级篮球赛,共13个班级参加.(1)、比赛积分规定:每场比赛都要分出胜负,胜一场积3分,负一场积1分.某班级在12场比赛中获得总积分为32分,问该班级胜负场数分别是多少?(2)、投篮得分规则:在3分线外投篮,投中一球可得3分,在3分线内(含3分线)投篮,投中一球可得2分,某班级在其中一场比赛中,共投中22个球(只有2分球和3分球),所得总分不少于50分,问该班级这场比赛中至少投中了多少个3分球?25. 综合与实践:

问题背景:数学小组发现国旗上五角星的五个角都是顶角为的等腰三角形,对此三角形产生了极大兴趣并展开探究.
探究发现:如图1,在中, , .
(1)、操作发现:将折叠,使边落在边上,点的对应点是点 , 折痕交于点 , 连接 , ,①;
②设 , 则(用含的式子表示);
(2)、进一步探究发现: , 这个比值被称为黄金比.请你在(1)的条件下,证明: .(3)、拓展应用:当等腰三角形的底与腰的比等于黄金比时,这个三角形叫黄金三角形.如图1中的是黄金三角形.
如图2,在菱形中, , , 求菱形较长对角线的长.
26. 如图,在平面直角坐标系中,抛物线过点 , 且交轴于点 , 两点,交轴于点 . (1)、求抛物线的表达式;(2)、点是直线上方抛物线上的一动点,过点作于点 , 过点作轴的平行线交直线于点 .
(1)、求抛物线的表达式;(2)、点是直线上方抛物线上的一动点,过点作于点 , 过点作轴的平行线交直线于点 .①当点P运动到抛物线顶点时,求此时的面积.
②点在运动的过程中,是否存在周长的最大值,若存在,请求出周长的最大值及此时点的坐标;若不存在,请说明理由.