贵州省名校协作体2024届高三下学期联考(二)数学试题
试卷更新日期:2024-04-08 类型:高考模拟
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 设集合 , , 则( )A、 B、 C、 D、2. 某同学一学期七次模拟考试数学成绩(满分150分)依次为88,98,112,106,122,118,110,则这名同学七次数学成绩的分位数为( )A、110 B、112 C、115 D、1183. 已知双曲线渐近线方程为 , 则的值为( )A、1 B、 C、 D、44. 已知数列满足 , 则( )A、0 B、1 C、 D、25. 若一圆锥的内切球半径为2,该圆锥的侧面展开图为一个半圆,则该圆锥的体积为( )A、 B、 C、 D、6. 已知 , , , 下列选项正确的是( )A、 B、 C、 D、7. 已知椭圆的左右焦点分别为 , , 点在直线上运动,则的最小值为( )A、7 B、9 C、13 D、158. 如图,射线与圆 , 当射线从开始在平面上按逆时针方向绕着原点匀速旋转( , 分别为和上的点,转动角度不超过)时,它被圆截得的线段长度为 , 其导函数的解析式为( )
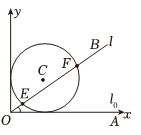 A、 B、 C、 D、
A、 B、 C、 D、二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
-
9. 已知复数 , 满足 , , 且 , 则( )A、 B、 C、若 , 则 D、10. 已知函数 , 则( )A、
 值域为
B、的最小正周期为
C、在上单调递减
D、
11. 已知正项数列满足 , 则( )A、为递增数列 B、 C、若 , 则存在大于1的正整数 , 使得 D、已知 , 则存
值域为
B、的最小正周期为
C、在上单调递减
D、
11. 已知正项数列满足 , 则( )A、为递增数列 B、 C、若 , 则存在大于1的正整数 , 使得 D、已知 , 则存 , 使得
, 使得
三、填空题:本题共3小题,每小题5分,共15分.
-
12. 已知命题 , 命题:函数有极小值点2,则是的条件(填“充要”、“充分不必要”、“必要不充分”、“既不充分也不必要”之一).13. 已知棱长为的正方体中,为棱上一动点,则的最小值为.14. 已知 , 分别为定义在上的偶函数和奇函数,且 , 若函数有唯一的零点,则.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
-
15. 在平面四边形中,平分 , .(1)、证明:与相等或互补;(2)、若 , 求的值.16. 如图,已知正方体 , 为的中点.
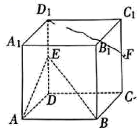 (1)、过作出正方体的截面 , 使得截面平行于平面 , 并说明理由;(2)、为线段上一点,且直线与截面所成角的正弦值为 , 求.17. 一枚质地均匀的小正方体,其中两个面标有数字1,两个面标有数字2,两个面标有数字3. 现将此正方体任意抛掷次,下落后均水平放置于桌面,记次上底面的数字之和为.(1)、当时,求的分布列与期望;(2)、设表示能被整除的概率,探索与的关系并求.18. 已知焦点在轴的等轴双曲线的虚轴长为 , 直线与交于 , 两点,线段的中点为.
(1)、过作出正方体的截面 , 使得截面平行于平面 , 并说明理由;(2)、为线段上一点,且直线与截面所成角的正弦值为 , 求.17. 一枚质地均匀的小正方体,其中两个面标有数字1,两个面标有数字2,两个面标有数字3. 现将此正方体任意抛掷次,下落后均水平放置于桌面,记次上底面的数字之和为.(1)、当时,求的分布列与期望;(2)、设表示能被整除的概率,探索与的关系并求.18. 已知焦点在轴的等轴双曲线的虚轴长为 , 直线与交于 , 两点,线段的中点为. (1)、若直线过的右焦点且 , 都在右支,求弦长的最小值;(2)、如图所示,虚线部分为双曲线与其渐近线之间的区域,点能否在虚线部分的区域内?请说明理由.19. 伯努利不等式又称贝努力不等式,由著名数学家伯努利发现并提出. 伯努利不等式在证明数列极限、函数的单调性以及在其他不等式的证明等方面都有着极其广泛的应用. 伯努利不等式的一种常见形式为:
(1)、若直线过的右焦点且 , 都在右支,求弦长的最小值;(2)、如图所示,虚线部分为双曲线与其渐近线之间的区域,点能否在虚线部分的区域内?请说明理由.19. 伯努利不等式又称贝努力不等式,由著名数学家伯努利发现并提出. 伯努利不等式在证明数列极限、函数的单调性以及在其他不等式的证明等方面都有着极其广泛的应用. 伯努利不等式的一种常见形式为:当 , 时, , 当且仅当或时取等号.
(1)、假设某地区现有人口100万,且人口的年平均增长率为 , 以此增长率为依据,试判断6年后该地区人口的估计值是否能超过107万?(2)、数学上常用表示 , , , 的乘积, , .(ⅰ)证明:;
(ⅱ)已知直线与函数的图象在坐标原点处相切,数列满足: , , 证明:.