四川省凉山州2024届高三二诊理科数学试题

试卷更新日期：2024-04-08 类型：高考模拟

进入出卷网下载

一、选择题（本大题共12小题，每题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）

1. 已知复数 $z = 1 + i$ ，则 $| \frac{z}{\bar{z}} | =$ （）

A、 $\frac{1}{2}$ B、1 C、 $\sqrt{2}$ D、2

查看试题解析
2. 已知集合 $A = {y | y = x + 1, - 1 \leq x \leq 1}$ ， $B = {x | x \leq a}$ ，若 $A \cup B = B$ ，则 $a$ 的取值范围为（）

A、 $[0, 2]$ B、 $[2, + \infty)$ C、 $(- \infty, 2]$ D、 $(- \infty, 1]$

查看试题解析
3. 已知 $A (2, 2)$ 在抛物线 $C : y^{2} = 2 p x$ 上，则 $A$ 到 $C$ 的焦点的距离为（）

A、 $1$ B、 $\frac{3}{2}$ C、 $2$ D、 $\frac{5}{2}$

查看试题解析
4. 已知 $X ∼ N (1, σ^{2})$ ，且 $P (x \leq a - 1) = P (x \geq 2)$ ，则在 ${(\sqrt{x} + 2 a)}^{5}$ 的展开式中， $x^{2}$ 的系数为（）

A、5 B、10 C、15 D、20

查看试题解析
5. 已知命题“ $\forall x \in R$ ， $s i n^{2} (π + x) + 2 c o s x + m \leq 0$ ”是假命题，则m的取值范围为（）

A、 $[- 2, + \infty)$ B、 $(- 2, + \infty)$ C、 $(- \infty, - 1)$ D、 $(- \infty, - 2]$

查看试题解析
6. 为了传承和弘扬雷锋精神，凝聚榜样力量.3月5日学雷锋纪念日来临之际，凉山州某中学举办了主题为“传承雷锋精神，践行时代力量”的征文比赛．此次征文共5个题目，每位参赛学生从中随机选取一个题目准备作文，则甲、乙，丙三位同学选到互不相同题目的概率为（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{9}{25}$ D、 $\frac{12}{25}$

查看试题解析
7. 已知正数 $a, b$ 满足 $a + 2 b = \int_{1}^{e} \frac{1}{x} d x$ ，则 $\frac{a b}{a^{2} + b}$ 的最大值为（）

A、 $\sqrt{2}$ B、 $2 \sqrt{2}$ C、 $\frac{1}{2 \sqrt{2} + 1}$ D、 $2 \sqrt{2} + 1$

查看试题解析
8. 若曲线 $y = \sqrt{x}$ 在 $x = 1$ 处的切线与圆C： $x^{2} + y^{2} = 4$ 交于A ， B两点，则 $| A B |$ 为（）

A、 $\sqrt{5}$ B、 $2 \sqrt{5}$ C、 $\frac{\sqrt{95}}{5}$ D、 $\frac{2 \sqrt{95}}{5}$

查看试题解析
9. 若实数x ， y满足不等式 $| x | + | y | \leq 2$ ，则 $x^{2} + y^{2} \leq 1$ 的概率为（）

A、 $\frac{π}{8}$ B、 $\frac{π}{6}$ C、 $\frac{π}{4}$ D、 $\frac{π}{3}$

查看试题解析
10. 已知在三棱锥 $P - A B C$ 中， $P A = \sqrt{3}$ ， $P B = P C = 2$ ，底面 $A B C$ 是边长为1的正三角形，则该三棱锥的外接球表面积为（）

A、 $3 π$ B、 $\frac{13 π}{3}$ C、 $4 π$ D、 $6 π$

查看试题解析
11. 若 $f (x) = x s i n x + c o s x - 1$ ， $x \in [- \frac{π}{2}, π]$ ，则函数 $f (x)$ 的零点个数为（）

A、0 B、1 C、2 D、3

查看试题解析
12. 已知点 $P (x, y)$ 是曲线 $y = x^{2}$ 上任意一点，则 $\frac{\sqrt{3} x + y + 1}{\sqrt{x^{2} + {(y + 1)}^{2}}}$ 的最大值为（）

A、 $\frac{2 \sqrt{5} - \sqrt{15}}{10}$ B、 $\frac{2 \sqrt{5} - \sqrt{15}}{5}$ C、 $\frac{\sqrt{15} + 2 \sqrt{5}}{10}$ D、 $\frac{\sqrt{15} + 2 \sqrt{5}}{5}$

查看试题解析

二、填空题（本题共4小题，每小题5分，共20分）

13. 设等差数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，若 $a_{3} + a_{5} = 10$ ， $a_{4} a_{9} = 50$ ，则 $S_{6} =$ ．

查看试题解析
14. 设 $△ A B C$ 的内角A ， B ， C的对边分别为a ， b ， c ，若 $\frac{a c o s B - b c o s A}{a c o s B + b c o s A} + \frac{b}{c} = 1$ ，则 $A =$ ．

查看试题解析
15. 如图，在平行四边形 $A B C D$ 中，E ， F分别是AD ， CD的中点，且 $B E = 6$ ， $B F = 3$ ， $〈 \vec{B E}, \vec{B F} 〉 = \frac{π}{3}$ ，则平行四边形 $A B C D$ 的面积为．

查看试题解析
16. 已知双曲线C： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0, b > 0)$ 的左、右焦点分别为 $F_{1}$ ， $F_{2}$ ．点A在C上，点B在y轴． ${\vec{F_{1} A}}^{2} = \vec{F_{1} A} \cdot (\vec{O A} - \vec{O B})$ ， $\vec{F_{2} A} = \frac{2}{5} \vec{B A}$ ，则C的渐近线方程为．

查看试题解析

三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17~21题为必考题，每个题考生都必须作答．第22、23题为选考题，考生根据要求作答．

17. 设等比数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ， $a_{1} = \frac{1}{2}$ ， $8 S_{6} = 7 S_{3}$ ．

(1)、求 $a_{n}$ ；

(2)、设 $b_{n} = \frac{l o g_{\frac{1}{2}} | a_{n} |}{| a_{n} |}$ ，求数列 ${b_{n}}$ 的前n项和 $T_{n}$ ．

查看试题解析
18. 常言道：文史不分家，其实数学与物理也不分家．“近代物理学之父”——牛顿大约在1671年，完成了《流数法和无穷级数》这部书，标志着微积分的正式创立．某学校课题小组针对“高中学生物理学习成绩与数学学习成绩的关系”进行了一系列的研究，得到了高中学生两学科的成绩具有线性相关的结论．现从该校随机抽取6名学生在一次考试中的物理和数学成绩，如表（单位：分）
物理成绩x
63
68
74
76
85
90
数学成绩y
90
95
110
110
125
130

(1)、经过计算，得到学生物理学习成绩x与数学学习成绩y满足回归方程 $\hat{y} = 1.5 x + m$ ．若某位学生的物理成绩为95分，请预测他的数学成绩；

(2)、若要从抽取的这6名学生中随机选出3名学生参加一项问卷调查，记数学成绩不低于100分的学生人数为X ，求X的分布列和数学期望．

查看试题解析
19. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为正方形， $P D ⊥ A D$ ，平面 $P A D ⊥$ 平面 $A B C D$ ， $P D = A D = 2$ ， $E$ 是 $P C$ 的中点，作 $E F ⊥ P B$ 交 $P B$ 于 $F$ ．

(1)、求证： $P A / /$ 平面 $B D E$ ；

(2)、求二面角 $F - C D - B$ 的正切值．

查看试题解析
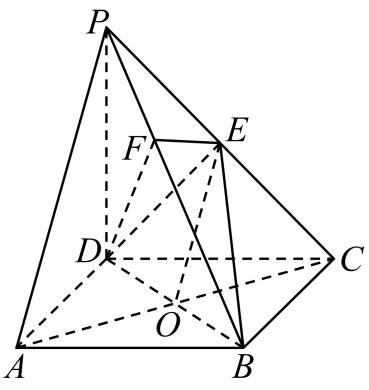20. 古希腊数学家阿基米德用“逼近法”得到：椭圆面积的4倍除以圆周率等于椭圆的长轴长与短轴长的积．已知 $F_{1}$ 是椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左焦点，且椭圆C的面积为 $2 \sqrt{3} π$ ，离心率为 $\frac{1}{2}$ ．

(1)、求椭圆C的标准方程；

(2)、设点 $A (t, 0)$ ， $(t > - 1)$ ，以 $F_{1} A$ 为直径的圆与椭圆C在x轴上方交于M ， N两点，求 $\frac{1}{t + 1} (| F_{1} M | + | F_{1} N |)$ 的值

查看试题解析
21. 已知函数 $f (x) = x + a s i n x$ ．

(1)、若函数 $f (x)$ 在R上是增函数，求a的取值范围；

(2)、设 $g (x) = x - \frac{1}{2} s i n x - l n x$ ，若 $g (x_{1}) = g (x_{2}) (x_{1} \neq x_{2})$ ，证明： $\sqrt{x_{1} x_{2}} < 2$ ．

查看试题解析
22. 在平面直角坐标系xOy中，曲线C的参数方程为 ${\begin{array}{l} x = \frac{2 - 2 t^{2}}{1 + t^{2}} \\ y = \frac{2 t}{1 + t^{2}} \end{array}$ ，（t为参数）．以坐标原点O为极点，x轴正半轴为极轴的极坐标系中，直线 $l_{1}$ 的极坐标方程为 $ρ c o s (θ - \frac{π}{4}) - 4 \sqrt{2} = 0$ ．

(1)、求曲线C的普通方程与直线 $l_{1}$ 的直角坐标方程；

(2)、若与直线 $l_{1}$ 垂直的直线 $l_{2}$ 交曲线C于A ， B两点，求 $| A B |$ 的最大值．

查看试题解析
23. 已知函数 $f (x) = | x |$ ．

(1)、求不等式 $f (l n x) \leq 1$ 的解集；

(2)、若函数 $g (x) = f (x) - f (x - 1)$ 的最小值为m ，且正数a ， b ， c满足 $a + b + c + 2 m = 0$ ，求 $a^{2} + 2 b^{2} + c^{2}$ 的最小值．

查看试题解析

物理成绩x	63	68	74	76	85	90
数学成绩y	90	95	110	110	125	130