吉林省长春市朝阳区七校联考2023-2024学年九年级下学期期初数学试题
试卷更新日期:2024-04-08 类型:月考试卷
一、选择题(每小题3分,共24分)
-
1. 中国人最早使用负数,可追溯到两千多年前的秦汉时期,-2的相反数是( )A、2 B、 C、-2 D、2. “奋斗者”号载人潜水器此前在马里亚纳海沟创造了10909米的我国载人深潜纪录,10909这个数用科学记数法表示为( )A、 B、 C、 D、3. 如图,由四个小正方体叠成的一个立体图形,它的俯视图是( )
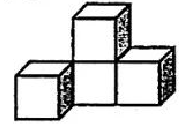 A、
A、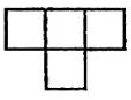 B、
B、 C、
C、 D、
D、 4. 不等式组的解集为( )A、 B、 C、 D、5. 已知一次函数 , 当时,函数y的最大值是( )A、3 B、5 C、0 D、76. 如图,已知直线 , 直线l与直线a、b分别交于点A、B , 分别以点A、B为圆心,大于的长为半径画弧,两弧相交于点M、N , 作直线MN , 交直线b于点C , 连接AC . 若 , 则∠ACB的大小为( )
4. 不等式组的解集为( )A、 B、 C、 D、5. 已知一次函数 , 当时,函数y的最大值是( )A、3 B、5 C、0 D、76. 如图,已知直线 , 直线l与直线a、b分别交于点A、B , 分别以点A、B为圆心,大于的长为半径画弧,两弧相交于点M、N , 作直线MN , 交直线b于点C , 连接AC . 若 , 则∠ACB的大小为( ) A、90° B、95° C、100° D、105°7. 如图,点A、B、C、D、E在上, , , 则圆心角∠AOB的大小为( )
A、90° B、95° C、100° D、105°7. 如图,点A、B、C、D、E在上, , , 则圆心角∠AOB的大小为( )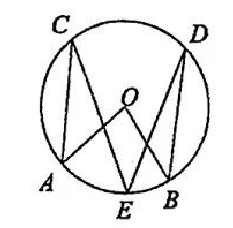 A、90° B、85° C、80° D、40°8. 如图,已知正方形ABCD的面积为4,它的两个顶点B , D是反比例函数的图象上两点.若点D的坐标是 , 则的值为( )
A、90° B、85° C、80° D、40°8. 如图,已知正方形ABCD的面积为4,它的两个顶点B , D是反比例函数的图象上两点.若点D的坐标是 , 则的值为( ) A、3 B、2 C、-3 D、-2
A、3 B、2 C、-3 D、-2二、填空题(每小题3分,共18分)
-
9. 有a名男生和b名女生在社区做义工,他们为建花坛搬砖.男生每人搬了40块,女生每人搬了30块,这a名男生和b名女生一共搬了块砖(用含a、b的代数式表示)10. 计算: .11. 二次函数与x轴有个交点.12. 如图,是有一个公共顶点O的两个全等正五边形,若将它们的其中一边都放在直线a上,则∠AOB的大小为 .
 13. 如图,在矩形ABCD中, , . 将此矩形折叠,使点C与点A重合,点D落在点处,折痕为EF , 则的面积为 .
13. 如图,在矩形ABCD中, , . 将此矩形折叠,使点C与点A重合,点D落在点处,折痕为EF , 则的面积为 . 14. 若抛物线恒在x轴下方,且符合条件的整数a有且只有一个,则实数c的最小值为 .
14. 若抛物线恒在x轴下方,且符合条件的整数a有且只有一个,则实数c的最小值为 .三、解答题(本大题共10小题,共78分)
-
15. 先化简,再求值: , 其中 .16. 在一个不透明的袋子中装有三个球,上面分别标有数字1、2、3,每个小球除数字不同外其余都相同.先将小球搅匀,小刚从袋中随机取出一个小球,记下数字后放回;再将小球搅匀,又从袋中随机取出一个小球记下数字,用画树状图(或列表)的方法,求小刚两次所记的数字之和等于4的概率.17. 小明准备抄写600个汉字练习书法,原计划每天抄写相同数量的汉字.在抄写100个汉字后,为了提前完成任务,每天的练字数量是原来的2倍,结果共用7天完成了任务.求小明原来每天抄写汉字的个数.18. 如图是由小正方形组成的6×7网格,每个小正方形的边长为1,每个小正方形的顶点称为格点.格点A、B、C在同一个圆上,只用无刻度直尺在分别在给定网格中按照下列要求作图,保留作图痕迹.
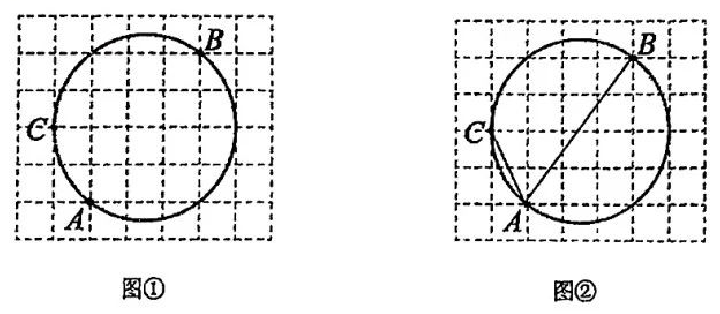 (1)、图①中,先画出圆心O , 然后在上画点D , 使 .(2)、图②中,在弧BC上画点E , 连接AE , 使AE平分∠CAB .19. 某校数学兴趣小组对九年级同学体育成绩进行调查,他们随机抽查n名同学体育测试成绩(由高到低分A、B、C , D四个等级),根据调查的数据绘制成如下的两幅统计图.
(1)、图①中,先画出圆心O , 然后在上画点D , 使 .(2)、图②中,在弧BC上画点E , 连接AE , 使AE平分∠CAB .19. 某校数学兴趣小组对九年级同学体育成绩进行调查,他们随机抽查n名同学体育测试成绩(由高到低分A、B、C , D四个等级),根据调查的数据绘制成如下的两幅统计图. (1)、n的值为 .(2)、扇形统计图中A所占的百分比a的值为 .(3)、若某校九年级共有1200名同学,请估计九年级同学体育测试成绩在B级以上(含B级)的约有多少名.20. 如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,海轮沿正南方向航行一段时间后,到达位于灯塔P的南偏东64°方向上的B处,求海轮所在的B处与灯塔P的距离.(结果精确到0.1海里)【参考数据: , , 】
(1)、n的值为 .(2)、扇形统计图中A所占的百分比a的值为 .(3)、若某校九年级共有1200名同学,请估计九年级同学体育测试成绩在B级以上(含B级)的约有多少名.20. 如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,海轮沿正南方向航行一段时间后,到达位于灯塔P的南偏东64°方向上的B处,求海轮所在的B处与灯塔P的距离.(结果精确到0.1海里)【参考数据: , , 】 21. 某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准,该市的用户每月应交水费y(元)与用水量x(立方米)之间的函数关系如图所示.
21. 某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准,该市的用户每月应交水费y(元)与用水量x(立方米)之间的函数关系如图所示. (1)、当用水18立方米以上时,求y与x之间的函数关系式.(2)、若小敏家某月交水费81元,求这个月用水量为多少立方米.22.
(1)、当用水18立方米以上时,求y与x之间的函数关系式.(2)、若小敏家某月交水费81元,求这个月用水量为多少立方米.22. (1)、【证明体验】如图①,AD为的角平分线, . 点E在AB上, .
(1)、【证明体验】如图①,AD为的角平分线, . 点E在AB上, .求证:DE平分∠ADB .
(2)、【思考探究】如图②,在(1)的条件下,F为AB上一点,连结FC交AD于点G . 若 , , , 求BC的长.
(3)、【拓展延伸】如图③.在四边形ABCD中,对角线AC平分∠BAD , . 点E在AC上, . 若 , . 直接写出CE的长.
23. 如图,在中, , , . 点P从点B出发,以每秒1个单位长度的速度沿BC向终点C运动.同时,点Q也从点B出发,以每秒3个单位长度的速度沿射线BC运动,当点,到达点C时,P、Q同时停止运动.以PQ为对角线作矩形PNQM , . 设矩形PNQM和重叠部分面积为 , 点P运动的时间为t秒. (1)、线段PQ的长为(用含t的代数式表示).(2)、当点N落在AC上时,求t的值.(3)、当点N在内部时,球S与t的之间函数关系式.(4)、连结AM , 当线段AM将矩形PNQM分成两部分的面积比1∶3时,直接写出t的值.24. 抛物线的顶点为 , 与y轴交于点 , 点D为抛物线对称轴上的一点,以AB , AD为邻边构造菱形ABCD .(1)、求抛物线的表达式.(2)、求点D坐标.(3)、点P为抛物线上的一个动点,设其横坐标为m .
(1)、线段PQ的长为(用含t的代数式表示).(2)、当点N落在AC上时,求t的值.(3)、当点N在内部时,球S与t的之间函数关系式.(4)、连结AM , 当线段AM将矩形PNQM分成两部分的面积比1∶3时,直接写出t的值.24. 抛物线的顶点为 , 与y轴交于点 , 点D为抛物线对称轴上的一点,以AB , AD为邻边构造菱形ABCD .(1)、求抛物线的表达式.(2)、求点D坐标.(3)、点P为抛物线上的一个动点,设其横坐标为m .①当与的面积之差的绝对值为定值时,求该定值.
②设点P关于抛物线对称轴的对称点为 , 当点P在第四象限,且等于菱形ABCD的一个内角时,直接写出m的值.