吉林省四平市伊通满族自治县2024年中考第一次模拟考试数学模拟试题

试卷更新日期：2024-04-08 类型：中考模拟

进入出卷网下载

一、选择题（每小题2分，共12分）

1. 长春市2月18日至2月21日天气预报的最高气温与最低气温如下表：
日期
2月18日
2月19日
2月20日
2月21日
最高气温/℃
8
$- 4$
$- 10$
$- 7$
最低气温/℃
$- 6$
$- 16$
$- 16$
$- 15$
其中温差最大的日期是（）

A、2月18日 B、2月19日 C、2月20日 D、2月21日

查看试题解析
2. m是两位数，n是一位数，若把m直接写在n后面，就成为一个三位数，这个三位数可表示成（）

A、 $10 n + m$ B、mn C、 $100 n + m$ D、 $100 m + n$

查看试题解析
3. 如图是一个几何体的表面展开图，则该几何体是（）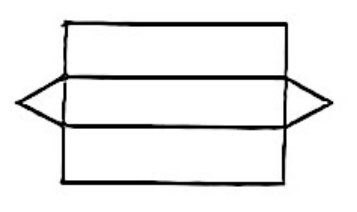

A、三棱锥 B、三棱柱 C、圆锥 D、长方体

查看试题解析
4. 如图是一款手推车的平面示意图，其中 $A B ∥ C D$ ， $∠ 1 = 30 °$ ， $∠ 2 = 70 °$ ，则 $∠ 3$ 的度数为（）

A、 $120 °$ B、 $130 °$ C、 $140 °$ D、 $150 °$

查看试题解析
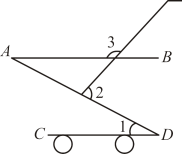5. 我国古代数学著作《九章算术》中有一道几何问题，其译文为：今有小城，东西7里，南北9里，各方中央开有城门．出东门15里有树．问出南门多少里见到树？如图，设AH为x里，则下面所列方程正确的是（）

A、 $\frac{x}{15} = \frac{3.5}{4.5}$ B、 $\frac{x}{4.5} = \frac{3.5}{15}$ C、 $\frac{4.5}{x + 4.5} = \frac{3.5}{15}$ D、 $\frac{x}{4.5} = \frac{3.5}{3.5 + 15}$

查看试题解析
6. 如图，在 $△ A O B$ 中， $∠ B = 30 °, A B = 3$ 以 $O$ 为圆心， $O A$ 为半径的 $⊙ O$ 交 $O B$ 于点 $C$ ，点D在⊙O上，连接CD、AD ．若 $∠ A D C = 30 °$ ．则⊙O的半径为（）

A、 $\sqrt{5}$ B、2 C、 $\sqrt{3}$ D、1

查看试题解析

二、填空题（每小题3分，共24分）

7. 计算： $(3 - π)^{0} + 2 s i n 30 ° =$ ．

查看试题解析
8. 分解因式： $a^{2} - 9 b^{2} =$ ．

查看试题解析
9. 若不等式 $x + 2 > 0$ 的解集在数轴上表示如图所示，则a的值为．

查看试题解析
10. 请填写一个常数，使得关于x的方程 $x^{2} - 4 x +$ =0有两个不相等的实数根．

查看试题解析
11. 如图，在 $△ A B C$ 中， $A B = A C, B C = 10$ ，由尺规作图的痕迹可求出BD的长为．

查看试题解析
12. 如图，在平面直角坐标系中，将直角三角板的 $60 °$ 角的顶点与坐标原点O重合，直角顶点B在x轴的负半轴上，顶点A在第三象限．将 $△ O A B$ 绕点O逆时针旋转一定角度得到 $△ O A^{'} B^{'}$ 使点B的对应点 $B^{'}$ 落在边OA上．若 $O B = 1$ ，则点 $A^{'}$ 的坐标为．

查看试题解析
13. 将一副三角尺按如图所示的方式摆放，使一块三角尺； $30 °$ 角的顶点和另一块三角尺的直角顶点重合，记为点O ，点C在边OB上，点A、D在OB的两侧，以O为圆心，3cm长为半径画⊙O ，分别交OA、OD于点E、F ，则 $\overset{⌢}{E F}$ 的长为（结果保留π）．

查看试题解析
14. 如图，在矩形ABCD中， $A D > A B$ ，将此矩形折叠，使点C与点A重合，折痕分别交BC、AD于点E、F ，连接EF ，点D的对应点为点 $D^{'}$ ．若AE平分 $∠ B A D, A B = 1$ ，则AF的长为．

查看试题解析

三、解答题（每小题5分，共20分）

15. 先化简，再求值： $\frac{a^{2} - 3 a}{a - 1} \div \frac{a^{2} - 9}{a - 1},$ 其中 $α = 2 .$

查看试题解析
16. 电动车操作简单、方便快捷、省时省力、性价比高，满足了人们对于短途出行的需要．小勇收集到四张正面分别印有台铃、小刀、爱玛、雅迪电动车图标的卡片（除图标外，其他完全相同），并在图标下方依次标记字母A、B、C、D ．将这四张卡片背面朝上，洗匀放好，从中随机抽取一张，不放回，再从中随机抽取一张．请用列表或画树状图的方法求抽到的两张卡片标记的字母恰好是C、D的概率．

查看试题解析
17. 2024年4月22日是第三十二届“世界水日”，长春市某校举行了主题为“强化依法治水，携手共护母亲河”的水资源保护知识宣传活动，学校为表彰在此次活动中表现突出的学生，购买了20个笔袋，30个笔筒，60个圆规作为奖品，共花费1020元，已知每个笔袋比每个圆规贵9元，每个笔筒的单价是每个圆规单价的2倍，求圆规的单价．

查看试题解析
18. 如图，AD⊥AE，AB⊥AC， AD＝AE，AB＝AC.求证：△ABD≌△ACE.

查看试题解析

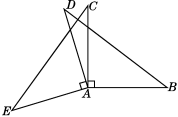
四、解答题（每小题7分，共28分）

19. 图①、图②、图③均是 $5 \times 5$ 的正方形网格，每个小正方形的顶点称为格点，小正方形的边长均为1．线段AB的端点在格点上．在图①、图②、图③中以AB为边各画一个三角形，使其面积依次为3、5和 $\frac{13}{2}$ ．只用无刻度的直尺按下列要求在给定的网格中画图，所画的图形的顶点均在格点上．不要求写出画法．保留作图痕迹．

查看试题解析
20. 如图，在平面直角坐标系中，O为坐标原点，线段AB的端点A、B的坐标分别为 $(1, 4)$ 、 $(4, 4)$ ，函数 $y = \frac{k}{x} (x > 0)$ 的图象交线段AB于点C ，且 $A C = 2 B C .$

(1)、求k的值；

(2)、将线段AB向上平移 $m (m > 0)$ 个单位长度后，得到线段 $A^{'} B^{'}$ ，若线段 $A^{'} B^{'}$ 的中点D在函数 $y = \frac{k}{x} (x > 0)$ 的图象上，求m的值．

查看试题解析
21. 为了解2018—2022年国有建设用地供应情况，根据统计信息绘制如下统计图．
根据统计图、回答以下问题：

(1)、2018—2022年国有建设用地中位数为万公顷；

(2)、2022年国有建设用地中，商服用地所占的百分比为；

(3)、对下列说法进行判断，正确的画“√”，错误的画“×”．
①从2019年开始国有建设用地逐年增加，增长量最高的年份为2019年（）
②在扇形统计图中，工矿仓储用地约占20万公顷（）

查看试题解析
22. 吉林市革命烈士纪念塔，是神圣而庄严的红色景点，是全国重点烈士纪念塔建筑物保护单位．某校数学兴趣活动小组来到此地测量塔高，如图，利用无人机获得相关数据如下：无人机在空中点P处，测得到地面的垂直距离PC为45m，测得塔顶A的俯角 $∠ A P D$ 的度数为61°，无人机到塔的水平距离PD为10m，求塔高AB（参考数据： $s i n 61 ° \approx 0.8746, c o s 61 ° \approx 0.4848, t a n 61 ° \approx 1.804$ ，结果精确到1m）．

查看试题解析

五、解答题（每小题8分，共16分）

23. 在一条笔直公路上A、B两地相距120km，甲骑自行车从A地驶往B地，乙骑自行车从B地驶往A地，甲比乙先出发．设甲、乙两人距A地的路程为y（千米），甲行驶的时间为x（小时）．y与x之间的关系如图所示．

(1)、甲骑自行车的速度是千米/小时，乙骑自行车的速度是千米/小时；

(2)、求乙骑自行车距A地的路程y（千米）与甲骑自行车行驶的时间x（小时）之间的函数关系式；

(3)、当甲、乙两人相距20千米时，直接写出x的值．

查看试题解析
24. 在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，点D为边BC上一点，连接AD ．

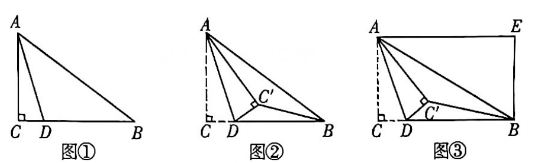(1)、【感知】如图①，若 $△ A B D$ 是等腰三角形， $A C = 6, A B = 10$ ，则CD的长为；

(2)、【探究】如图②，将 $△ A C D$ 沿AD翻折，得到 $△ A C^{'} D$ ，连接 $B C^{'}$ ．若 $△ B D C^{'}$ 是以 $D C^{'}$ 为直角边的直角三角形， $A C = 6, A B = 10$ ，求CD的长；

(3)、【拓展】如图③，将 $△ A C D$ 沿AD翻折，得到 $△ A C^{'} D$ ，连接 $B C^{'}$ ．以AC、BC为边作矩形ACBE ．若点D、 $C^{'}$ 、E在一条直线上，且 $A C = 6, B C = 10$ ，直接写出CD的长．

查看试题解析

六、解答题（每小题10分，共20分）

25. 如图，在菱形ABCD中，对角线 $B D = 6, ∠ A = 60 °$ ．点P从点A出发，沿AB以每秒1个单位长度的速度匀速运动，到点B停止．过点P作 $P Q ⊥ A B$ ，交折线 $A D - D B$ 于点Q ，以PQ、PB为边作矩形PQEB ，设矩形PQEB与 $△ A B D$ 重叠部分图形的面积为S ，点P的运动时间为 $t (s) (0 < t < 6)$ ．

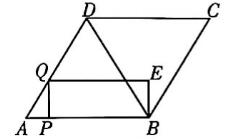(1)、用含t的代数式表示PB的长；

(2)、求S与t之间的函数关系式，并写出自变量t的取值范围；

(3)、作射线CE ，当CE截矩形PQEB所得的图形存在轴对称图形时，直接写出t的值．

查看试题解析
26. 如图，在平面直角坐标系中， $O$ 为坐标原点，点P、Q均在抛物线 $y = x^{2} + b x - 3$ 上，其横坐标分别为m、 $1 - 2 m$ ，抛物线上点P、Q之间的部分记为图象G ．过点Q作 $Q A ⊥ x$ 轴于点A ．该抛物线的顶点B的横坐标为1．

(1)、求此抛物线的解析式；

(2)、连接OP ，当 $O P ⊥ x$ 轴时，求点Q的坐标；

(3)、当点B是图象G的最低点，且 $A Q = 3$ 时，求图象G最高点与最低点的纵坐标的差；

(4)、当点B是图象G的最低点，且点P到AQ的距离等于AQ时，直接写出m的值．

查看试题解析

日期	2月18日	2月19日	2月20日	2月21日
最高气温/℃	8	$- 4$	$- 10$	$- 7$
最低气温/℃	$- 6$	$- 16$	$- 16$	$- 15$