吉林省长春市榆树市红星乡2023-2024学年九年级下学期月考数学试卷(3月)
试卷更新日期:2024-04-08 类型:月考试卷
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 方程3+9=0的根为( )A、3 B、-3 C、±3 D、无实数根2. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、3. 下列说法正确的是( )A、“买中奖率为的奖券张,一定中奖”是必然事件 B、“汽车累积行驶 , 从未出现故障”是不可能事件 C、天气预报说“明天的降水概率为”,意味着明天一定下雨 D、“清明时节雨纷纷”为随机事件4. 如图,张老汉想用长为米的栅栏,再借助房屋的外墙外墙足够长围成一个面积为平方米的矩形羊圈 , 并在边上留一个米宽的门建在处,门用其他材料 , 设的长为米,则下面所列方程正确的是( )
 A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 如图,四边形 和四边形 是以点 为位似中心的位似图形,若 ,四边形 的面积等于4,则四边形 的面积为( )
A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 如图,四边形 和四边形 是以点 为位似中心的位似图形,若 ,四边形 的面积等于4,则四边形 的面积为( ) A、3 B、4 C、6 D、97. 如图,中, , 利用尺规在 , 上分别截取 , , 使;分别以 , 为圆心、以大于的长为半径作弧,两弧在内交于点;作射线交于点若 , , , 为上一动点,则的最小值为( )
A、3 B、4 C、6 D、97. 如图,中, , 利用尺规在 , 上分别截取 , , 使;分别以 , 为圆心、以大于的长为半径作弧,两弧在内交于点;作射线交于点若 , , , 为上一动点,则的最小值为( )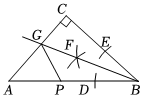 A、 B、 C、 D、8. 若抛物线的对称轴为轴,且点在该抛物线上,则的值为( )A、 B、 C、 D、
A、 B、 C、 D、8. 若抛物线的对称轴为轴,且点在该抛物线上,则的值为( )A、 B、 C、 D、二、填空题:本题共6小题,每小题3分,共18分。
-
9. 若关于x的一元二次方程x2+mx+2n=0有一个根是2,则m+n= .10. 如果关于的一元二次方程有两个同号实数根,则的取值范围是 .11. 已知二次函数的函数值与自变量的部分对应值如表:
则这个二次函数图象的对称轴是直线 .
12. 如图,是的切线,是切点,连结、若 , 则的大小为 度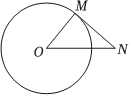 13. 如图,在平面直角坐标系中,P是第一象限的点,其坐标为(x , 8),且OP与x轴正半轴的夹角α的正切值为 , 则x的值为 .
13. 如图,在平面直角坐标系中,P是第一象限的点,其坐标为(x , 8),且OP与x轴正半轴的夹角α的正切值为 , 则x的值为 . 14. 如图,△ABC与△DEF是位似图形,点O是位似中心,OB:BE=1,若S△ABC=2,则S△DEF= .
14. 如图,△ABC与△DEF是位似图形,点O是位似中心,OB:BE=1,若S△ABC=2,则S△DEF= .
三、计算题:本大题共1小题,共5分。
-
15. 解方程: .
四、解答题:本题共11小题,共73分。解答应写出文字说明,证明过程或演算步骤。
-
16. 计算: .17. 先化简,再求值: , 其中 .18. 甲、乙两人同在如图所示的地下车库等电梯,已知他们分别在至层的任意一层出电梯.
车库
(1)、如果甲在层出电梯,那么乙和甲在同一层楼出电梯的概率是;(2)、请你用画树状图或列表法求出甲、乙在同一楼层出电梯的概率.19. 即将到来的年是中国农历甲辰龙年某商场用元购进了一批“小金龙”布偶玩具,面市后供不应求,商场又用元购进了第二批这种玩具,所购数量是第一批购进数量的倍,但每件的进价贵了元求商场购进第一批“小金龙”每件的进价.20. 如图,在平面直角坐标系中,每个小正方形的边长都为 , 和的顶点都在格点上,回答下列问题: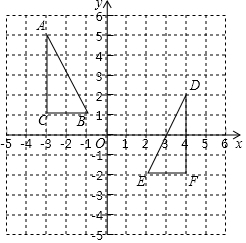 (1)、可以看作是经过若干次图形的变化平移、轴对称、旋转得到的,写出一种由得到的过程:;(2)、画出绕点逆时针旋转的图形;(3)、在中,点所形成的路径的长度为 .21. 某校生物小组有一块长32m,宽20m的矩形试验田,为了管理方便,准备沿平行于两边的方向纵、横各开辟一条等宽的小道.要使种植面积为540m2 , 小道的宽应是多少?
(1)、可以看作是经过若干次图形的变化平移、轴对称、旋转得到的,写出一种由得到的过程:;(2)、画出绕点逆时针旋转的图形;(3)、在中,点所形成的路径的长度为 .21. 某校生物小组有一块长32m,宽20m的矩形试验田,为了管理方便,准备沿平行于两边的方向纵、横各开辟一条等宽的小道.要使种植面积为540m2 , 小道的宽应是多少? 22. 如图, , 直线 , 交于点 , 且分别与直线 , , 交于点、、和点、、 , 已知 , , , , 求的长度是?
22. 如图, , 直线 , 交于点 , 且分别与直线 , , 交于点、、和点、、 , 已知 , , , , 求的长度是? 23. 已知如图,抛物线的顶点D的坐标为(1,-4),且与y轴交于点C(0,-3).
23. 已知如图,抛物线的顶点D的坐标为(1,-4),且与y轴交于点C(0,-3). (1)、求该函数的关系式;(2)、求该抛物线与x轴的交点A,B的坐标.24. 如图,是等腰直角三角形, , 点为的中点,与相切于点 , 连结交于点 .
(1)、求该函数的关系式;(2)、求该抛物线与x轴的交点A,B的坐标.24. 如图,是等腰直角三角形, , 点为的中点,与相切于点 , 连结交于点 .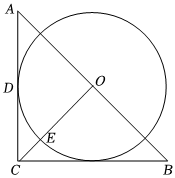 (1)、判断所在直线与的位置关系,并说明理由.(2)、若的半径为 , 求的长结果保留25. 如图,一位足球运动员在距离球门中心水平距离8米的A处射门,球沿一条抛物线运动.当球运动的水平距离为6米时,达到最大高度3米.
(1)、判断所在直线与的位置关系,并说明理由.(2)、若的半径为 , 求的长结果保留25. 如图,一位足球运动员在距离球门中心水平距离8米的A处射门,球沿一条抛物线运动.当球运动的水平距离为6米时,达到最大高度3米. (1)、建立图中所示的平面直角坐标系,求抛物线所对应的函数表达式;(2)、已知球门高为2.44米,通过计算判断这位运动员能否将球射进球门.26. 已知抛物线、、是常数, , 自变量与函数值的部分对应值如表:
(1)、建立图中所示的平面直角坐标系,求抛物线所对应的函数表达式;(2)、已知球门高为2.44米,通过计算判断这位运动员能否将球射进球门.26. 已知抛物线、、是常数, , 自变量与函数值的部分对应值如表: (1)、根据以上信息,可知抛物线开口向 ,对称轴为直线 .(2)、求抛物线的解析式和的值.(3)、将抛物线的图象记为 , 将绕点旋转后的图象记为 , 、合起来得到的图象记为 , 完成以下问题:
(1)、根据以上信息,可知抛物线开口向 ,对称轴为直线 .(2)、求抛物线的解析式和的值.(3)、将抛物线的图象记为 , 将绕点旋转后的图象记为 , 、合起来得到的图象记为 , 完成以下问题:
若直线与函数有且只有两个交点,直接写出的取值范围.
若对于函数上的两点、 , 当 , 时,总有 , 直接写出的取值范围.
-