吉林省2023-2024学年八年级下学期第一次月考数学试题
试卷更新日期:2024-04-08 类型:月考试卷
一、选择题
-
1. 若二次根式在实数范围内有意义,则m的取值范围是( )A、 B、 C、 D、2. 计算的结果是( )A、6 B、 C、 D、3. 下列根式是最简二次根式的是( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,在中, , 平分交边于点D , 若 , 则线段的长为( )
 A、 B、1 C、2 D、36. 如图①,四个全等的直角三角形围成一个大正方形,中间是个小正方形,这个图形是我国汉代赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.连接四条线段得到如图②的新的图案,如果图①中的直角三角形的长直角边为 , 短直角边为 , 则图中的阴影部分的周长为( )
A、 B、1 C、2 D、36. 如图①,四个全等的直角三角形围成一个大正方形,中间是个小正方形,这个图形是我国汉代赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.连接四条线段得到如图②的新的图案,如果图①中的直角三角形的长直角边为 , 短直角边为 , 则图中的阴影部分的周长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每小题3分,共24分)
-
7. 计算: = .8. 计算的结果是 .9. 化简: .10. 若最简二次根式与可以合并,则11. 如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形B、C、D的面积依次为4、3、9,则正方形A的面积为 .
 12. 如图,在平面直角坐标系中,点A的坐标为 , 以点O为圆心,的长为半径画弧,交y轴的正半轴于点B , 则点B的坐标为 .
12. 如图,在平面直角坐标系中,点A的坐标为 , 以点O为圆心,的长为半径画弧,交y轴的正半轴于点B , 则点B的坐标为 . 13. 如图,正方形的顶点A在数轴上对应的数为2,以点A为圆心,长为半径画圆弧,交数轴于点E(点E位于点A的左侧).若正方形的面积为2,则点E表示的数为 .
13. 如图,正方形的顶点A在数轴上对应的数为2,以点A为圆心,长为半径画圆弧,交数轴于点E(点E位于点A的左侧).若正方形的面积为2,则点E表示的数为 . 14. 如图,在中, , 点、为边上
14. 如图,在中, , 点、为边上 点,连接、 , 将边沿翻折,使点的对称点在边上的点处;再将边沿翻折,使点的对称点落在的延长线上的点处.若 , , 则的长为 .
点,连接、 , 将边沿翻折,使点的对称点在边上的点处;再将边沿翻折,使点的对称点落在的延长线上的点处.若 , , 则的长为 . 
三、解答题(每小题5分,共20分)
-
15. 计算:16. 计算:()().17. 计算:18. 若 , , 求的值.
四、解答题(每小题7分,共28分)
-
19. 某工程队需穿过某座大山修一条隧道 , 如图,为了测量隧道的长度,在山的另一侧水平地面上取了一点C、在隧道的延长线上取了点D , 测量得知, , 米,米,请你求出隧道的长.
 20. 图①、图②、图③均是的正方形网格,每个小正方形的边长均为1.线段的端点均在格点上,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上.
20. 图①、图②、图③均是的正方形网格,每个小正方形的边长均为1.线段的端点均在格点上,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上. (1)、在图①中以为边画一个等腰三角形,使它的三边长均是无理数;(2)、在图②中以为边画一个直角三角形,使它的直角边之比为;(3)、在图③中以为边画一个钝角三角形,使它的钝角为 .21. 在中, , , , , 为垂足.求的长.
(1)、在图①中以为边画一个等腰三角形,使它的三边长均是无理数;(2)、在图②中以为边画一个直角三角形,使它的直角边之比为;(3)、在图③中以为边画一个钝角三角形,使它的钝角为 .21. 在中, , , , , 为垂足.求的长. 22. 如图在四边形中,为对角线, , , , .
22. 如图在四边形中,为对角线, , , , . (1)、求四边形的周长;(2)、求四边形的面积.
(1)、求四边形的周长;(2)、求四边形的面积.五、解答题(每小题8分,共16分)
-
23. 阅读下列解题过程
例:若代数式的值是2,求a的取值范围
解:原式 ,
当时,原式 , 解得(舍去);
当时,原式 , 符合条件;
当时,原式 , 解得(舍去).
的取值范围是 .
上述解题过程主要运用了分类讨论的方法,请你根据上述理解,解答下列问题:
(1)、当时,化简: .(2)、若 , 求a的取值范围.24.(1)、【感知】如图①,在中, , 点D为边上的一点,连接 . 若是等腰三角形, , , 则的长为;(2)、【探究】如图②,将沿翻折,得到 , 连接 . 若是以为直角边的直角三角形, , , 求的长.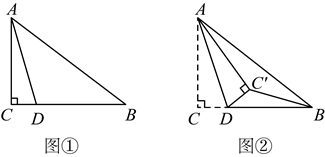
六、解答题(每小题10分,共20分)
-
25.
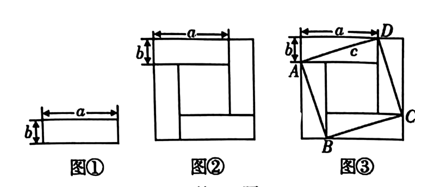 (1)、【操作】将如图①所示的四张大小形状完全相同的长方形纸片按如图②方式拼成一个大正方形,利用面积的不同表示方法可以表示的代数恒等式;(2)、【应用】按图③方式顺次连接图②中四张长方形纸片的对角线,得到正方形 , 设 , 利用正方形的面积的表示方法证明勾股定理;(3)、【拓展】如图③,若 , 中间小正方形的面积是 , 求的值.26. 如图,在中, , 的面积为 , 是边上的高,动点P从点B出发,以每秒1个单位长度的速度沿匀速向终点A运动,点P不与点A、B重合,连接、 . 设点P的运动时间为t秒.
(1)、【操作】将如图①所示的四张大小形状完全相同的长方形纸片按如图②方式拼成一个大正方形,利用面积的不同表示方法可以表示的代数恒等式;(2)、【应用】按图③方式顺次连接图②中四张长方形纸片的对角线,得到正方形 , 设 , 利用正方形的面积的表示方法证明勾股定理;(3)、【拓展】如图③,若 , 中间小正方形的面积是 , 求的值.26. 如图,在中, , 的面积为 , 是边上的高,动点P从点B出发,以每秒1个单位长度的速度沿匀速向终点A运动,点P不与点A、B重合,连接、 . 设点P的运动时间为t秒. (1)、求的长;(2)、用含t的代数式表示的长;(3)、在点P运动的过程中,不再添加其他辅助线的情况下,当图中存在等腰直角三角形时,求的面积;(4)、点P在上运动,不再添加其他辅助线的情况下,当图中存在以点P为顶点的等腰三角形.且不是直角三角形时,直接写出t的值.
(1)、求的长;(2)、用含t的代数式表示的长;(3)、在点P运动的过程中,不再添加其他辅助线的情况下,当图中存在等腰直角三角形时,求的面积;(4)、点P在上运动,不再添加其他辅助线的情况下,当图中存在以点P为顶点的等腰三角形.且不是直角三角形时,直接写出t的值.