初中数学同步训练必刷培优卷（北师大版七年级下册 4.5利用三角形全等测距离）

试卷更新日期：2024-04-03 类型：同步测试

进入出卷网下载

一、选择题

1. 王强同学用10块高度都是2cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚可以放进一个等腰直角三角板（AC=BC ，　∠ACB=90°）点C在DE上，点A和B分别与木墙的顶端重合，则两堵木墙之间的距离为（）

A、10cm B、14cm C、20cm D、6cm

查看试题解析
2. 程老师制作了如图1所示的学具，用来探究“边边角条件是否可确定三角形的形状”问题，操作学具时，点Q在轨道槽AM上运动，点P既能在以A为圆心、以8为半径的半圆轨道槽上运动，也能在轨道槽QN上运动，图2是操作学具时，所对应某个位置的图形的示意图．

有以下结论：

①当∠PAQ=30°，PQ=6时，可得到形状唯一确定的△PAQ

②当∠PAQ=30°，PQ=9时，可得到形状唯一确定的△PAQ

③当∠PAQ=90°，PQ=10时，可得到形状唯一确定的△PAQ

④当∠PAQ=150°，PQ=12时，可得到形状唯一确定的△PAQ

其中所有正确结论的序号是（）

A、②③ B、③④ C、②③④ D、①②③④

查看试题解析
3. 如图，小明站在堤岸的A点处，正对他的S点停有一艘游艇.他想知道这艘游艇距离他有多远，于是他沿堤岸走到电线杆B旁，接着再往前走相同的距离到达C点.然后他向左直行，当看到电线杆与游艇在一条直线上时停下来，此时他位于D点.那么C，D两点间的距离就是在A点处小明与游艇的距离.在这个问题中，可作为证明 $△ S A B ≌ △ D C B$ 的依据的是（）

A、 $S A S$ 或 $S S S$ B、 $A A S$ 或 $S S S$ C、 $A S A$ 或 $A A S$ D、 $A S A$ 或 $S A S$

查看试题解析
4. 某大学计划为新生配备如图①所示的折叠凳.图②是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计)，其中凳腿AB和CD的长相等，O是它们的中点.为了使折叠凳坐着舒适，厂家将撑开后的折叠凳宽度AD设计为30 cm，则由以上信息可推得CB的长度也为30 cm，依据是（）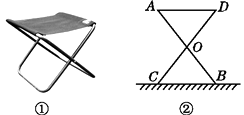

A、SAS B、ASA C、SSS D、AAS

查看试题解析
5. 如图，强强想测量旗杆AB的高度，旗杆对面有一高为18米的大楼CD ，大楼与旗杆相距28米（BD＝28米），在大楼前10米的点P处，测得∠APC＝90°，且AB⊥BD ， CD⊥BD ，则旗杆AB的高为（　　）

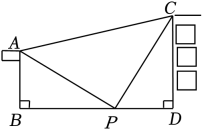A、8米 B、10米 C、12米 D、18米

查看试题解析
6. 题目：“如图，∠B＝45°，BC＝2，在射线BM上取一点A ，设AC＝d ，若对于d的一个数值，只能作出唯一一个△ABC ，求d的取值范围．”对于其答案，甲答： $d \geq 2$ ，乙答：d＝1.6，丙答： $d = \sqrt{2}$ ，则正确的是（）

A、只有甲答的对 B、甲、丙答案合在一起才完整 C、甲、乙答案合在一起才完整 D、三人答案合在一起才完整

查看试题解析
7. 如图，在 $3 \times 3$ 的网格中，每一个小正方形的边长都是1，点 $A$ ， $B$ ， $C$ ， $D$ 都在格点上，连接 $A C$ ， $B D$ 相交于 $P$ ，那么 $∠ A P B$ 的大小是（）

A、 $80 °$ B、 $60 °$ C、 $45 °$ D、 $30 °$

查看试题解析
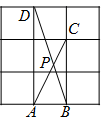8.
如图，正方形ABCD中，点E，F分别在BC，CD上，△AEF是等边三角形，连接AC交EF于点G，下列结论：①CE=CF，②∠AEB=75°，③AG=2GC，④BE+DF=EF，⑤S_△_CEF=2S_△_ABE ，其中结论正确的个数为（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

9.
如图，在正n边形（n为整数，且n≥4）绕点A顺时针旋转60°后，发现旋转前后两图形有另一交点O，连接AO，我们称AO为“叠弦”；再将“叠弦”AO所在的直线绕点A逆时针旋转60°后，交旋转前的图形于点P，连接PO，我们称∠OAB为正n边形的“叠弦角”，△AOP为“叠弦三角形”．以下说法，正确的是．（填番号）
①在图1中，△AOB≌△AOD'；
②在图2中，正五边形的“叠弦角”的度数为360°；
③“叠弦三角形”不一定都是等边三角形； ④正n边形的“叠弦角”的度数为60°﹣ $\frac{180 °}{n}$ ．

查看试题解析
10. 如图，已知长方形ABCD的边长AB=20cm，BC=16cm，点E在边AB上，AE=6cm，如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动，同时，点Q在线段CD上从点C到点D运动．则当△BPE与△CQP全等时，时间t为 s．

查看试题解析
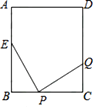11. 某数学兴趣小组利用全等三角形的知识测试某小河的宽度，如图，点 $A ， B ， C$ 是小河两边的三点，在河边 $A B$ 下方选择一点，使得 $∠ B A D = ∠ B A C ， ∠ A B D = ∠ A B C$ ，若测得 $A B = 10$ 米， $△ A B D$ 的面积为30平方米，则点 $C$ 到 $A B$ 的距离为米．

查看试题解析
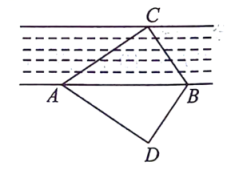12. 如图，两根旗杆间相距12m，某人从点B沿BA走向点A，一段时间后他到达点M，此时他仰望旗杆的顶点C和D，两次视线的夹角为90°，且CM=DM，已知旗杆AC的高为3m，该人的运动速度为1m/s，则这个人运动到点M所用时间是

查看试题解析

三、作图题

13. 如图，某公园有一个人工湖，王平和李楠两人想知道这个人工湖的长度 $A B$ ，但无法直接度量，于是他们准备用所学知识，设计测量方案进行测量．已知 $B P$ 为垂直于 $A B$ 的一条小路，且小路两侧除人工湖所占区域外，其他区域均可随意到达，他们两人所带的测量工具只有一根足够长的皮卷尺，请你帮王平和李楠两人设计一种测量方案：

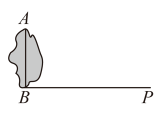(1)、请在图中画出测量示意图并写出测量数据（线段长度可用 $a$ 、 $b$ 、 $c$ ……表示）；（不要求写出测量过程）

(2)、根据你的测量方案数据，计算出这个人工湖的长度 $A B$ ．

查看试题解析

四、解答题

14.
【阅读理解题】初二（1）班同学到野外上数学活动课，为测量池塘两端A、B的距离，设计了如下方案：
（Ⅰ）如图1，先在平地上取一个可直接到达A、B的点C，连接AC、BC，并分别延长AC至D，延长BC至E，使 $D C = A C$ ， $E C = B C$ ，最后测出DE的距离即为AB的长；
（Ⅱ）如图2，先过B点作AB的垂线BF，再在BF上取C、D两点使 $B C = C D$ ，接着过D作BD的垂线DE，交AC的延长线于E，则测出DE的长即为AB的距离.
阅读后回答下列问题：

(1)、方案（Ⅰ）是否可行?请直接说出结论.

(2)、方案（Ⅱ）是否可行?请说明理由.

(3)、方案（Ⅱ）中作 $B F ⊥ A B$ ， $E D ⊥ B F$ 目的是；

(4)、若仅满足 $∠ A B D = ∠ B D E \neq 90 °$ ，方案（Ⅱ）是否成立?.

查看试题解析
15. 阿进在物理课上学习了发声物体的振动实验后，对其作了进一步的探究：如图，在一个支架的横杆点 $O$ 处用一根细绳悬挂一个小球 $A$ ，小球 $A$ 可以自由摆动， $O A$ 表示小球静止时的位置.当阿进用发声物体靠近小球时，小球从 $O A$ 摆到 $O B$ 位置，此时过点 $B$ 作 $B D ⊥ O A$ 于点 $D$ .当小球撰到 $O C$ 位置时， $O B$ 与 $O C$ 恰好垂直（图中的 $A$ ， $B$ ， $O$ ， $C$ 在同一平面上），过点 $C$ 作 $C E ⊥ O A$ 于点 $E$ .

(1)、求证： $∠ C O E = ∠ B$ ；

(2)、若阿进测得 $B D = 8 c m$ ， $O A = 17 c m$ ，求 $A E$ 的长.

查看试题解析
16. 如图

(1)、问题背景：如图 $1$ ，在四边形 $A B C D$ 中， $A B = A D$ ， $∠ B A D = 120 °$ ， $∠ B = ∠ A D C = 90 °$ ， $E$ ， $F$ 分别是 $B C$ ， $C D$ 上的点，且 $∠ E A F = 60 °$ ，探究图中线段 $B E$ ， $E F$ ， $F D$ 之间的数量关系．小王同学探究此问题的方法是：延长 $F D$ 到点 $G$ ，使 $D G = B E$ ，连接 $A G$ ，先证明 $△ A B E ≌ △ A D G$ ，再证明 $△ A E F ≌ △ A G F$ ，可得出结论，他的结论应是， ▲ ，请说明理由；

(2)、实际应用：如图 $2$ ，在新修的小区中，有块四边形绿化 $A B C D$ ，四周修有步行小径，且 $A B = A D$ ， $∠ B + ∠ D = 180 °$ ，在小径 $B C$ ， $C D$ 上各修一凉亭 $E$ ， $F$ ，在凉亭 $E$ 与 $F$ 之间有一池塘，不能直接到达．经测量得到 $∠ E A F = \frac{1}{2} ∠ B A D$ ， $B E = 10$ 米， $D F = 15$ 米，试求两凉亭之间的距离 $E F$ ．

查看试题解析