初中数学同步训练必刷基础卷(北师大版七年级下册 4.5利用三角形全等测距离)
试卷更新日期:2024-04-03 类型:同步测试
一、选择题
-
1. 如图,七1班同学要测量河两岸相对的两点、的距离,用合适的方法使 , , 因此测得的长就是的长,在这里判定 , 最恰当的理由是( )
 A、 B、 C、 D、2. 如图,将两根同样的钢条和的中点固定在一起,使其可以绕着点自由转动,就做成了一个测量工件内径的工具.这时根据 , 的长就等于工件内槽的宽 , 这里判定的依据是( )
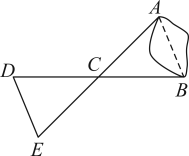
A、 B、 C、 D、2. 如图,将两根同样的钢条和的中点固定在一起,使其可以绕着点自由转动,就做成了一个测量工件内径的工具.这时根据 , 的长就等于工件内槽的宽 , 这里判定的依据是( ) A、边角边 B、角边角 C、边边边 D、角角边3. 如图,为了测出池塘两端A,B间的距离,小铱在地面上取一个可以直接到达A点和B点的点 , 连接并延长到 , 使;连接并延长到 , 使 , 连接并和测量出它的长度,小铱认为的长度就是A,B间的距离,她是根据来判断的 , 那么判定这两个三角形全等的依据是( ).
A、边角边 B、角边角 C、边边边 D、角角边3. 如图,为了测出池塘两端A,B间的距离,小铱在地面上取一个可以直接到达A点和B点的点 , 连接并延长到 , 使;连接并延长到 , 使 , 连接并和测量出它的长度,小铱认为的长度就是A,B间的距离,她是根据来判断的 , 那么判定这两个三角形全等的依据是( ).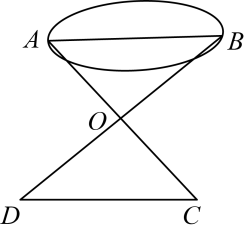 A、 B、 C、 D、4. 如图,要测量河两岸相对的两点A、B的距离,先在河岸BF上取两点C、D,使CD=BC,再作DE⊥BF,垂足为D,使A、C、E三点在一条直线上,测得ED=30米,因此AB的长是( )
A、 B、 C、 D、4. 如图,要测量河两岸相对的两点A、B的距离,先在河岸BF上取两点C、D,使CD=BC,再作DE⊥BF,垂足为D,使A、C、E三点在一条直线上,测得ED=30米,因此AB的长是( ) A、10米 B、20米 C、30米 D、40米5. 如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分线的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )
A、10米 B、20米 C、30米 D、40米5. 如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分线的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )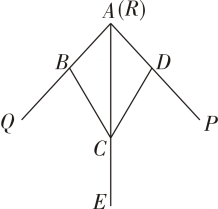 A、SAS B、ASA C、AAS D、SSS6. 在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=a,EF=b,圆形容器的壁厚是( )
A、SAS B、ASA C、AAS D、SSS6. 在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=a,EF=b,圆形容器的壁厚是( )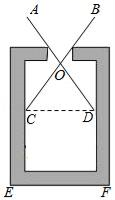 A、a B、b C、b﹣a D、 (b﹣a)7.
A、a B、b C、b﹣a D、 (b﹣a)7.如图,某同学把一块三角形的玻璃打破成了三块,现在他要到玻璃店去配一块完全一样形状的玻璃,那么最省事的办法是带( )去配.
 A、① B、② C、③ D、①和②8.
A、① B、② C、③ D、①和②8.一块三角形玻璃样板不慎被小强同学碰破,成了四片完整四碎片(如图所示),聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板.你认为下列四个答案中考虑最全面的是( )
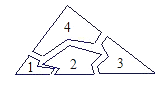 A、带其中的任意两块去都可以 B、带1、2或2、3去就可以了 C、带1、4或3、4去就可以了 D、带1、4或2、4或3、4去均可
A、带其中的任意两块去都可以 B、带1、2或2、3去就可以了 C、带1、4或3、4去就可以了 D、带1、4或2、4或3、4去均可二、填空题
-
9. 如图,小明与小红玩跷跷板游戏,如果跷跷板的支点(即跷跷板的中点)至地面的距离是50cm,当小红从水平位置下降30cm时,这时小明离地面的高度是cm.
 10. 有一座锥形小山,如图,要测量锥形小山两端、的距离,先在平地上取一个可以直接到达和的点 , 连接并延长到 , 使 , 连接并延长到 , 使 , 连接 , 量出的长为 , 则锥形小山两端、的距离为
10. 有一座锥形小山,如图,要测量锥形小山两端、的距离,先在平地上取一个可以直接到达和的点 , 连接并延长到 , 使 , 连接并延长到 , 使 , 连接 , 量出的长为 , 则锥形小山两端、的距离为 11. 小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块)你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带.依据
11. 小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块)你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带.依据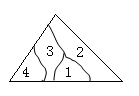 12. 如图,小明站在堤岸的A点处,正对他的S点停有一艘游艇.他想知道这艘游艇距离他有多远,于是他沿堤岸走到电线杆B旁,接着再往前走相同的距离,到达C点.然后他向左直行,当看到电线杆与游艇在一条直线上时停下来,此时他位于D点.小明测得C、D间的距离为90米,则在A点处小明与游艇的距离为米.
12. 如图,小明站在堤岸的A点处,正对他的S点停有一艘游艇.他想知道这艘游艇距离他有多远,于是他沿堤岸走到电线杆B旁,接着再往前走相同的距离,到达C点.然后他向左直行,当看到电线杆与游艇在一条直线上时停下来,此时他位于D点.小明测得C、D间的距离为90米,则在A点处小明与游艇的距离为米. 13. 用同种材料制成的金属框架如图所示,已知 , , , 其中的周长为24cm, , 则制成整个金属框架所需这种材料的长度为cm.
13. 用同种材料制成的金属框架如图所示,已知 , , , 其中的周长为24cm, , 则制成整个金属框架所需这种材料的长度为cm.
三、解答题