初中数学同步训练必刷培优卷(北师大版七年级下册 4.1认识三角形)
试卷更新日期:2024-04-03 类型:同步测试
一、选择题
-
1. 如图, , , , 若 , 则的度数为( )
 A、 B、 C、 D、2. 如图,下列命题:
A、 B、 C、 D、2. 如图,下列命题:
①若∠1=∠2,则∠D=∠4;
②若∠C=∠D,则∠4=∠C;
③若∠A=∠F,则∠1=∠2;
④若∠1=∠2,∠C=∠D,则∠A=∠F;
⑤若∠C=∠D,∠A=∠F,则∠1=∠2.
其中正确的个数为( )
A、1 B、2 C、3 D、43. 下列说法中:①三角形三边高线的交点一定在三角形内部;②八边形有20条对角线;③两个连续偶数的平方差一定是8的倍数;④无论x取何值,代数式的值一定是正数.正确的有( )A、②④ B、①② C、①③ D、③④4. 如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺ABC固定不动,将含角的三角尺DBE绕顶点顺时针转动(转动角度小于).当DE与三角尺ABC的其中一条边所在的直线互相平行时,的度数是( )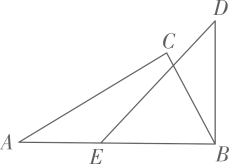 A、或或 B、或或 C、或或 D、或或5. 用12根等长的火柴棒拼成一个三角形,火柴棒不允许剩余,重叠和折断,则能摆出不同的三角形的个数是( )A、1个 B、2个 C、3个 D、4个6. 如图, , ∠M=44°,AN平分∠BAM,CN平分∠DCM,则∠N等于( )
A、或或 B、或或 C、或或 D、或或5. 用12根等长的火柴棒拼成一个三角形,火柴棒不允许剩余,重叠和折断,则能摆出不同的三角形的个数是( )A、1个 B、2个 C、3个 D、4个6. 如图, , ∠M=44°,AN平分∠BAM,CN平分∠DCM,则∠N等于( )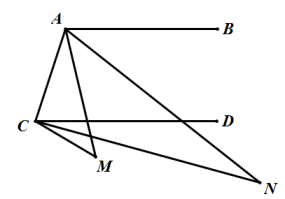 A、21.5° B、21° C、22.5° D、22°7. 平面内,将长分别为1,5,1,1,d的线段,顺次首尾相接组成凸五边形(如图),则d可能是()
A、21.5° B、21° C、22.5° D、22°7. 平面内,将长分别为1,5,1,1,d的线段,顺次首尾相接组成凸五边形(如图),则d可能是()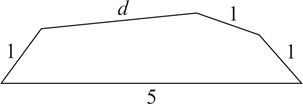 A、1 B、2 C、7 D、88. 将一副三角板按如图放置,有下列结论:①若∠2=30°,则AC∥DE;
A、1 B、2 C、7 D、88. 将一副三角板按如图放置,有下列结论:①若∠2=30°,则AC∥DE;②∠BAE+∠CAD=180°;③若BC∥AD,则∠2=30°;④若∠CAD=150°,则
∠4=∠C.其中正确的是( )
 A、①②④ B、①③④ C、②③④ D、①②③④
A、①②④ B、①③④ C、②③④ D、①②③④二、填空题
-
9. 如图,和分别是的内角平分线和外角平分线,是的角平分线,是的角平分线,是的角平分线,是的角平分线,若 , 则 .
 10. 如图,在四边形中,如果 , , P是边上一点,平分交边于点E,平分交边于点F.以下四个结论:①;②;③若 , 则;④若平分 , 则 . 其中正确的是(填写正确的序号).
10. 如图,在四边形中,如果 , , P是边上一点,平分交边于点E,平分交边于点F.以下四个结论:①;②;③若 , 则;④若平分 , 则 . 其中正确的是(填写正确的序号).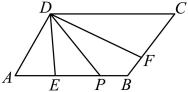 11. 如图,直线 , 一副三角板按如图1摆放,其中 , , . 保持三角板不动,现将三角板绕点以每秒的速度顺时针旋转,如图2,设旋转时间为t秒,且 , 则经过秒边与三角板的一条直角边(边 , )平行.
11. 如图,直线 , 一副三角板按如图1摆放,其中 , , . 保持三角板不动,现将三角板绕点以每秒的速度顺时针旋转,如图2,设旋转时间为t秒,且 , 则经过秒边与三角板的一条直角边(边 , )平行. 12. 图1是一款落地的平板支撑架,AB,BC是可转动的支撑杆.调整支撑杆使得其侧面示意图如图2所示,此时平板 , , , 则;现将支撑杆AB调整至图3所示位置,调整过程中 , 大小不变, , 再顺时针调整平板DE至 , 使得 , 则.
12. 图1是一款落地的平板支撑架,AB,BC是可转动的支撑杆.调整支撑杆使得其侧面示意图如图2所示,此时平板 , , , 则;现将支撑杆AB调整至图3所示位置,调整过程中 , 大小不变, , 再顺时针调整平板DE至 , 使得 , 则.

三、作图题
-
13. 仅用无刻度的直尺作出符合下列要求的图形.
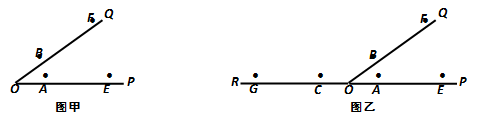 (1)、如图甲,在射线OP、OQ上已截取OA=OB,OE=OF.试过点O作射线OM,使得OM将∠POQ平分;(2)、如图乙,在射线OP、OQ、OR上已截取OA=OB=OC,OE=OF=OG(其中OP、OR在同一根直线上). 试过点O作一对射线OM、ON,使得OM⊥ON.
(1)、如图甲,在射线OP、OQ上已截取OA=OB,OE=OF.试过点O作射线OM,使得OM将∠POQ平分;(2)、如图乙,在射线OP、OQ、OR上已截取OA=OB=OC,OE=OF=OG(其中OP、OR在同一根直线上). 试过点O作一对射线OM、ON,使得OM⊥ON.四、综合题
-
14.
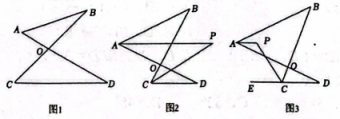 (1)、已知:如图(1)的图形我们把它称为“8字形”,请你说明:.(2)、如图(2),AP,CP分别平分 , 若 , 求的度数;(3)、如图(3),直线AP平分平分的外角 , 猜想与、的数量关系并证明.15. 阅读下列材料并解答问题:在一个三角形中,如果一个内角的度数是另一个内角度数的3倍,那么这样的三角形我们称为“梦想三角形”例如:一个三角形三个内角的度数分别是120°,40°,20°,这个三角形就是一个“梦想三角形”.反之,若一个三角形是“梦想三角形”,那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍.
(1)、已知:如图(1)的图形我们把它称为“8字形”,请你说明:.(2)、如图(2),AP,CP分别平分 , 若 , 求的度数;(3)、如图(3),直线AP平分平分的外角 , 猜想与、的数量关系并证明.15. 阅读下列材料并解答问题:在一个三角形中,如果一个内角的度数是另一个内角度数的3倍,那么这样的三角形我们称为“梦想三角形”例如:一个三角形三个内角的度数分别是120°,40°,20°,这个三角形就是一个“梦想三角形”.反之,若一个三角形是“梦想三角形”,那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍. (1)、如果一个“梦想三角形”有一个角为108°,那么这个“梦想三角形”的最小内角的度数为(2)、如图1,已知∠MON=60°,在射线OM上取一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(点C不与O、B重合),若∠ACB=80°.判定△AOB、△AOC是否是“梦想三角形”,为什么?(3)、如图2,点D在△ABC的边上,连接DC,作∠ADC的平分线交AC于点E,在DC上取一点F,使得∠EFC+∠BDC=180°,∠DEF=∠B.若△BCD是“梦想三角形”,求∠B的度数.
(1)、如果一个“梦想三角形”有一个角为108°,那么这个“梦想三角形”的最小内角的度数为(2)、如图1,已知∠MON=60°,在射线OM上取一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(点C不与O、B重合),若∠ACB=80°.判定△AOB、△AOC是否是“梦想三角形”,为什么?(3)、如图2,点D在△ABC的边上,连接DC,作∠ADC的平分线交AC于点E,在DC上取一点F,使得∠EFC+∠BDC=180°,∠DEF=∠B.若△BCD是“梦想三角形”,求∠B的度数.
-