湖南省衡阳市衡山县2023-2024学年八年级上学期数学期末考试试卷
试卷更新日期:2024-04-03 类型:期末考试
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 下列实数中,属于无理数的是( )A、 B、 C、 D、2. 如图,屋顶钢架外框是等腰三角形,其中 , 工人师傅在焊接立柱时,只用找到的中点 , 这就可以说明竖梁垂直于横梁了,工人师傅这种操作方法的依据是( )
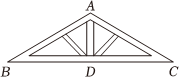 A、等边对等角 B、等角对等边
A、等边对等角 B、等角对等边
C、垂线段最短 D、等腰三角形“三线合一”3. 已知 , 则( )A、y B、 C、 D、4. 若多项式可因式分解为 , 则的值为( )A、 B、 C、 D、5. 下列各式中,不能用平方差公式计算的是( )A、 B、 C、 D、6. 如图,用直尺和圆规作已知角的平分线的示意图,则说明∠CAD=∠DAB的依据是( ) A、SAS B、ASA C、AAS D、SSS7. 若关于的多项式中不含一次项,则的值为( )A、 B、 C、 D、8. 如果多项式是一个完全平方式,则的值是( )A、 B、 C、 D、9. 如图,中, , 、的垂直平分线分别交于点、 , 则的度数为( )
A、SAS B、ASA C、AAS D、SSS7. 若关于的多项式中不含一次项,则的值为( )A、 B、 C、 D、8. 如果多项式是一个完全平方式,则的值是( )A、 B、 C、 D、9. 如图,中, , 、的垂直平分线分别交于点、 , 则的度数为( )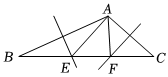 A、 B、 C、 D、10. 给出下列命题:
A、 B、 C、 D、10. 给出下列命题:
每个命题都有逆命题;
任意一个无理数的绝对值都是正数;
没有立方根;
有一个角是的三角形是等边三角形.
其中真命题的个数为( )A、个 B、个 C、个 D、个11. 计算:1252-50×125+252=( )A、100 B、150 C、10000 D、2250012. 在数学拓展课上,有两个全等的含角的直角三角板 , 重叠在一起李老师将三角板绕点顺时针旋转保持 , 延长线段 , 与线段的延长线交于点如图所示 , 随着的增大,的值( )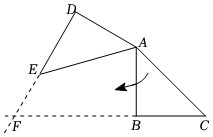 A、一直变小 B、保持不变 C、先变小,后变大 D、一直变大
A、一直变小 B、保持不变 C、先变小,后变大 D、一直变大二、填空题:本题共6小题,每小题3分,共18分。
-
13. 的算术平方根是 .14. .15. 计算: .16. 已知a+ =3,则a2+ 的值是 .17. 如图,在中, , , , 则的度数是 .
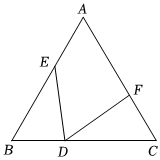 18. 如图所示, , , 则下列结论:
18. 如图所示, , , 则下列结论:
;≌;;;
≌其中正确的有 .
请把正确答案的序号填在横线上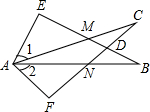
三、解答题:本题共6小题,共66分。解答应写出文字说明,证明过程或演算步骤。
-
19. 请将下列式子进行因式分解:
(1)、;
(2)、 .20. 已知: , 求代数式的值.21. 为了更好地开展课后服务,满足同学们的需求某中学在全校学生中随机抽查了部分学生参加音乐、体育、美术、书法等活动项目每人只限一项的情况下面是根据调查结果绘制的两幅不完整的统计图,请根据图中提供的信息,回答下列问题: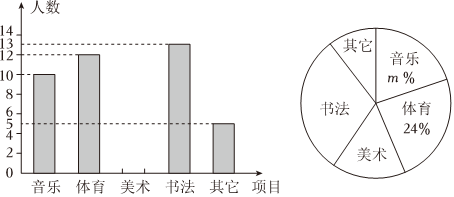 (1)、本次抽样调查中共抽取了名学生;(2)、扇形统计图中的值是;(3)、请求出扇形统计图中“美术”对应的扇形圆心角度数.22. 王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC , ∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合.
(1)、本次抽样调查中共抽取了名学生;(2)、扇形统计图中的值是;(3)、请求出扇形统计图中“美术”对应的扇形圆心角度数.22. 王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC , ∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合.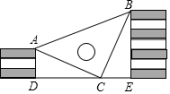 (1)、求证:△ADC≌△CEB;(2)、求两堵木墙之间的距离.23. 勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一.它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.
(1)、求证:△ADC≌△CEB;(2)、求两堵木墙之间的距离.23. 勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一.它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.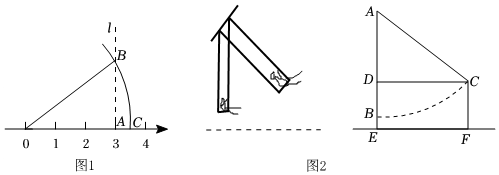 (1)、应用场景在数轴上画出表示无理数的点.
(1)、应用场景在数轴上画出表示无理数的点.
如图 , 在数轴上找出表示的点 , 过点作直线垂直于 , 在上取点 , 使 , 以原点为圆心,为半径作弧,则弧与数轴的交点表示的数是 .(2)、应用场景解决实际问题.
如图 , 秋千静止时,踏板离地的垂直高度 , 将它往前推至处时,水平距离 , 踏板离地的垂直高度 , 它的绳索始终拉直,求绳索的长.24. 综合与探究:问题情景:如图所示,已知,在中, , , 是的中线,过点作 , 垂足为 , 且交于点 .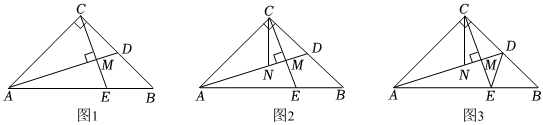 (1)、探究一小虎通过度量发现 , 请你帮他说明理由;
(1)、探究一小虎通过度量发现 , 请你帮他说明理由;
(2)、探究二小明在图中添加了一条线段 , 且平分交于点 , 如图所示,即可得 , 符合题意吗?请说明理由;
(3)、探究三小刚在的基础上,连接 , 如图所示,若 , , 求的面积.