吉林省延边朝鲜族自治州敦化市(第四学区)2023-2024学年七年级上学期数学期末考试试卷
试卷更新日期:2024-04-03 类型:期末考试
一、选择题(每小题2分,共12分)
-
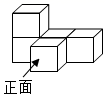
1. 若有理数a与3互为相反数,则a的值是( )A、3 B、-3 C、 D、-2. 在朱自清的《春》中描写春雨“像牛毛、像花针、像细丝,密密麻麻地斜织着”的语句,这里把雨看成了线,这说明了( )A、点动成线 B、线动成面 C、面动成体 D、两点确定一条直线3. 如图是由几个相同的小正方体堆砌成的几何体,从上面看到该几何体的形状图是( )
 A、
A、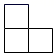 B、
B、 C、
C、 D、
D、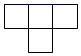 4. 如图所示,数轴上点A、点B对应的有理数分别为m、n , 下列说法中正确的是 ( )
4. 如图所示,数轴上点A、点B对应的有理数分别为m、n , 下列说法中正确的是 ( ) A、m+n<0 B、m-n>0 C、mn>0 D、∣m∣-∣n∣<05. 第19届亚运会于2023年9月23日至10月8日在中国浙江省杭州市举行,杭州奥体 博览城成为杭州2022年亚运会的主场馆. 杭州奥体博览城核心区占地154. 37公顷,建筑总面积2 720 000平方米,将数据2 720 000用科学记数法表示为( )A、0. 272×107 B、2. 72×106 C、27. 2×105 D、272×1046. 《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?设合伙人数为x人,所列方程正确的是( )A、5x - 45 = 7x - 3 B、5x + 45 = 7x + 3 C、 D、
A、m+n<0 B、m-n>0 C、mn>0 D、∣m∣-∣n∣<05. 第19届亚运会于2023年9月23日至10月8日在中国浙江省杭州市举行,杭州奥体 博览城成为杭州2022年亚运会的主场馆. 杭州奥体博览城核心区占地154. 37公顷,建筑总面积2 720 000平方米,将数据2 720 000用科学记数法表示为( )A、0. 272×107 B、2. 72×106 C、27. 2×105 D、272×1046. 《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?设合伙人数为x人,所列方程正确的是( )A、5x - 45 = 7x - 3 B、5x + 45 = 7x + 3 C、 D、二、填空题(每小题3分,共24分)
-
7. 中国人很早开始使用负数,中国古代数学著作《九章算术》的“方程”一章中,在世界数学史上首次正式引入负数.如果收入100元记作+100元,那么支出80元可以表示为.8. 若∠ α= 60°38' , 则它的补角的度数是.9. 如果2x2y与x2yb-1的和为单项式,那么b的值是.10. 如图,直线AB经过点O , 射线OA是北偏东40°方向,则射线OB的方位角是.
 11. 如果x = 5是关于x的方程mx-7(x-1)= m-2(x+m)的解,则m =.12. 若规定“※”的运算法则为:a※b =ab-1,例如: 2※3 = 2×3-1 = 5,则(-1)※4 =.13. 当时间8:30时,此刻钟表盘面上时针与分针的夹角是度.14. 两条线段,一条长6cm,另一条长10cm,将它们一端重合且放在同一条直线上,则这两条线段的中点之间的距离是cm.
11. 如果x = 5是关于x的方程mx-7(x-1)= m-2(x+m)的解,则m =.12. 若规定“※”的运算法则为:a※b =ab-1,例如: 2※3 = 2×3-1 = 5,则(-1)※4 =.13. 当时间8:30时,此刻钟表盘面上时针与分针的夹角是度.14. 两条线段,一条长6cm,另一条长10cm,将它们一端重合且放在同一条直线上,则这两条线段的中点之间的距离是cm.三、解答题(每小题5分,共20分)
-
15. 计算:20-11+(-10)-(-12).16. 计算:-14-18÷(-3)2×(-2)3.17. 解方程:.18. 根据下列要求画图:
 (1)、连接AB;(2)、画射线OA;(3)、作直线OB.19. 一个锐角的度数为x°,且比它的余角的2倍小30°.(1)、这个锐角的余角为度(用含x的式子表示);(2)、求这个锐角的度数.20. 先化简,再求值:6(x2-2x)+2(1+3x-2x2),其中x =.21. 如图,M是线段AC的中点,点B在线段AC上,且AB=4cm,BC=2AB,求线段MC和线段BM的长.
(1)、连接AB;(2)、画射线OA;(3)、作直线OB.19. 一个锐角的度数为x°,且比它的余角的2倍小30°.(1)、这个锐角的余角为度(用含x的式子表示);(2)、求这个锐角的度数.20. 先化简,再求值:6(x2-2x)+2(1+3x-2x2),其中x =.21. 如图,M是线段AC的中点,点B在线段AC上,且AB=4cm,BC=2AB,求线段MC和线段BM的长. 22. 某食品厂从生产的食品中抽出样品20袋,检测每袋的质量是否符合标准,超过的部分用正数表示,不足的部分用负数表示,记录如表:
22. 某食品厂从生产的食品中抽出样品20袋,检测每袋的质量是否符合标准,超过的部分用正数表示,不足的部分用负数表示,记录如表:与标准质量的差值(克)
-5
-2
0
1
3
6
袋数(袋)
2
4
5
5
1
3
(1)、若每袋标准质量为250克,则这批抽样检测的样品的总质量是多少克?;(2)、若该食品的包装袋上标有产品合格要求为“净重(250±2)克”,则这批样品的合格率为多少?23. 在某年全国足球甲级联赛的前11场比赛中,A队保持连续不败,共积分23分,按比赛规则,胜一场得3分,平一场得1分,那么该队比赛共胜了几场?(列方程解答)24. 问题:如图,已知△ACD和△BCE是两个直角三角形,∠ACD = 90°,∠BCE = 90°. (1)、证明:如图,因为∠ACD = 90°,∠BCE = 90°,
(1)、证明:如图,因为∠ACD = 90°,∠BCE = 90°,所以∠ACE+ ▲ = ∠BCD+ ▲ = 90°.
所以∠ACE = ▲ ;
(2)、解:因为∠ACB = 150°,∠ACD = 90°,所以∠BCD = ▲ - ▲ = ▲ °.
所以∠DCE = ▲ -∠BCD = ▲ °.
25. 已知点B、O、C在同一条直线上,∠AOB=α(0°<α<60°). (1)、如图①,若∠AOD= 90°,∠COD = 65°,则α =;(2)、如图②,若∠BOD = 90°,∠BOE = 50°,OA平分∠DOE , 求α;(3)、如图③,若∠AOD与∠AOB互余,∠BOE也与∠AOB互余,请在图③中画出 符合条件的射线OE加以计算后,直接写出∠DOE的度数(用含α的式子表示).26. 如图,已知数轴上点A表示的数为-2,点B是数轴上在点A右侧的一点,且A、B两点间的距离为4.动点Р从点A出发,以每秒3个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)、如图①,若∠AOD= 90°,∠COD = 65°,则α =;(2)、如图②,若∠BOD = 90°,∠BOE = 50°,OA平分∠DOE , 求α;(3)、如图③,若∠AOD与∠AOB互余,∠BOE也与∠AOB互余,请在图③中画出 符合条件的射线OE加以计算后,直接写出∠DOE的度数(用含α的式子表示).26. 如图,已知数轴上点A表示的数为-2,点B是数轴上在点A右侧的一点,且A、B两点间的距离为4.动点Р从点A出发,以每秒3个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒. (1)、数轴上点B表示的数是 , 点Р表示的数是(用含t的代数式表示);(2)、动点Q从点B出发,以每秒5个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,求:
(1)、数轴上点B表示的数是 , 点Р表示的数是(用含t的代数式表示);(2)、动点Q从点B出发,以每秒5个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,求:①当点Р运动多少秒时,点P与点Q重合?
②当点Р运动多少秒时,点P与点Q之间的距离为3个单位长度?(②直接写出t的值).