吉林省名校调研2023-2024学年九年级上学期数学期中考试试卷
试卷更新日期:2024-04-03 类型:期中考试
一、选择题:本题共6小题,每小题2分,共12分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 抛物线y=3(x+4)2+2的顶点坐标是( )A、(2,4) B、(2,-4) C、(4,2) D、(-4,2)2. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 一元二次方程:的根是( )A、 B、 C、 , D、 ,4. 如图,AB是⊙O的直径,C , D是⊙O上两点,若∠AOC=140°,则∠BDC=( )
3. 一元二次方程:的根是( )A、 B、 C、 , D、 ,4. 如图,AB是⊙O的直径,C , D是⊙O上两点,若∠AOC=140°,则∠BDC=( )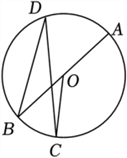 A、20° B、40° C、55° D、70°5. 如图,在中, , , , 将绕点按逆时针方向旋转得到 , 此时点恰好在边上,连接 , 则的长为( )
A、20° B、40° C、55° D、70°5. 如图,在中, , , , 将绕点按逆时针方向旋转得到 , 此时点恰好在边上,连接 , 则的长为( )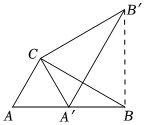 A、 B、 C、 D、6. 如图是二次函数的部分图象,顶点坐标为下列结论:;;;方程有两个相等的实数根其中所有正确结论的序号是( )
A、 B、 C、 D、6. 如图是二次函数的部分图象,顶点坐标为下列结论:;;;方程有两个相等的实数根其中所有正确结论的序号是( )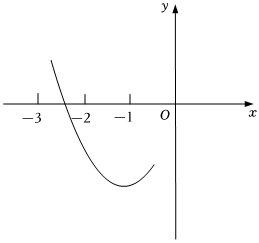 A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题共8小题,每小题3分,共24分。
-
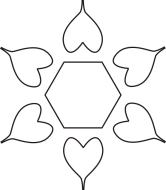
7. 在平面直角坐标系中,点关于原点对称的点的坐标是 .8. 若二次函数有最大值,则“”中可填的数字是 .9. 如图,该图形绕其中心旋转能与其自身完全重合,则其旋转角最小为 度
 10. 已知关于x的一元二次方程2x2-x+m=0有两个不相等的实数根,则m的取值范围是 .11. 如图,四边形是的内接四边形,是的直径, , 则的度数是 .
10. 已知关于x的一元二次方程2x2-x+m=0有两个不相等的实数根,则m的取值范围是 .11. 如图,四边形是的内接四边形,是的直径, , 则的度数是 . 12. 将抛物线先向左平移个单位长度,再向下平移个单位长度,得到的抛物线的解析式是 .13. 如图,直线、垂直相交于点 , 曲线关于点成中心对称,点的对称点是点 , 于点 , 于点 . 若 , , 则阴影部分的面积之和为 .
12. 将抛物线先向左平移个单位长度,再向下平移个单位长度,得到的抛物线的解析式是 .13. 如图,直线、垂直相交于点 , 曲线关于点成中心对称,点的对称点是点 , 于点 , 于点 . 若 , , 则阴影部分的面积之和为 . 14. 如图是一个圆弧形隧道的截面,若路面宽为 , 高为 , 则此圆弧形隧道的半径
14. 如图是一个圆弧形隧道的截面,若路面宽为 , 高为 , 则此圆弧形隧道的半径
三、解答题:本题共12小题,共84分。解答应写出文字说明,证明过程或演算步骤。
-
15. 用配方法解方程: .16. 如图,在中, , 求证: .
 17. 已知抛物线的顶点坐标是 , 且经过点求该抛物线的解析式.18. 图、图都是由边长为的小菱形构成的网格,每个小菱形的顶点称为格点.已知点、、均在格点上,分别按下列要求作一个四边形,使、、这三个点在这个四边形的边包括顶点上,且四边形的顶点在格点上.
17. 已知抛物线的顶点坐标是 , 且经过点求该抛物线的解析式.18. 图、图都是由边长为的小菱形构成的网格,每个小菱形的顶点称为格点.已知点、、均在格点上,分别按下列要求作一个四边形,使、、这三个点在这个四边形的边包括顶点上,且四边形的顶点在格点上.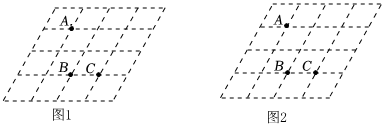 (1)、在图中作一个四边形,使其是中心对称图形,但不是轴对称图形;(2)、在图中作一个四边形,使其既是轴对称图形又是中心对称图形.19. 某水果商场经销一种高档水果,原价每千克元,连续两次降价后每千克元,若每次下降的百分率相同,求每次下降的百分率.20. 如图,在平面直角坐标系中,点 , 把绕原点逆时针旋转,得到 , 点分别为点、旋转后的对应点旋转角记为:
(1)、在图中作一个四边形,使其是中心对称图形,但不是轴对称图形;(2)、在图中作一个四边形,使其既是轴对称图形又是中心对称图形.19. 某水果商场经销一种高档水果,原价每千克元,连续两次降价后每千克元,若每次下降的百分率相同,求每次下降的百分率.20. 如图,在平面直角坐标系中,点 , 把绕原点逆时针旋转,得到 , 点分别为点、旋转后的对应点旋转角记为: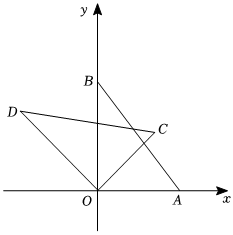 (1)、当时,求点的坐标;(2)、当轴时,直接写出的值.21. 如图,现打算用的篱笆围成一个“日”字形菜园含隔离栏 , 菜园的一面靠墙 , 墙可利用的长度为篱笆的宽度忽略不计(1)、菜园面积可能为吗?若可能,求边长的长,若不可能,说明理由.(2)、因场地限制,菜园的宽度不能超过 , 求该菜园面积的最大值.22. 如图,是的直径,是的中点,于 , 交于点 .
(1)、当时,求点的坐标;(2)、当轴时,直接写出的值.21. 如图,现打算用的篱笆围成一个“日”字形菜园含隔离栏 , 菜园的一面靠墙 , 墙可利用的长度为篱笆的宽度忽略不计(1)、菜园面积可能为吗?若可能,求边长的长,若不可能,说明理由.(2)、因场地限制,菜园的宽度不能超过 , 求该菜园面积的最大值.22. 如图,是的直径,是的中点,于 , 交于点 .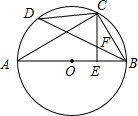 (1)、求证:;(2)、若 , , 求的半径.23. 如图,在平面直角坐标系中,点 , 抛物线交轴于 , 两点,交轴于点 .
(1)、求证:;(2)、若 , , 求的半径.23. 如图,在平面直角坐标系中,点 , 抛物线交轴于 , 两点,交轴于点 .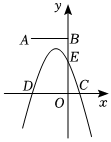 (1)、求抛物线的解析式;(2)、当时,求的最小值;(3)、连接 , 若二次函数的图象向上平移个单位时,与线段有一个公共点,结合函数图象,直接写出的取值范围.24. 旋转是一种重要的图形变换,当图形中有一组邻边相等时,往往可以通过旋转解决问题.如图 , 在四边形中, , , , , .
(1)、求抛物线的解析式;(2)、当时,求的最小值;(3)、连接 , 若二次函数的图象向上平移个单位时,与线段有一个公共点,结合函数图象,直接写出的取值范围.24. 旋转是一种重要的图形变换,当图形中有一组邻边相等时,往往可以通过旋转解决问题.如图 , 在四边形中, , , , , .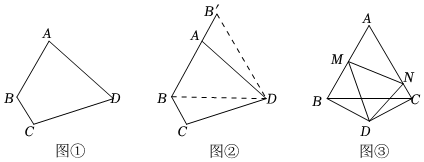 (1)、如图 , 在图的基础上连接 , 由于 , 所以可将绕点顺时针方向旋转 , 得到 , 则的形状是
(1)、如图 , 在图的基础上连接 , 由于 , 所以可将绕点顺时针方向旋转 , 得到 , 则的形状是
(2)、在的条件下,求四边形的面积;(3)、【类比应用】如图 , 等边的边长为 , 是顶角的等腰三角形,以为顶点作一个的角,角的两边分别交于点 , 交于点 , 连接 , 求的周长.25. 如图,在中, , , , 点为边的中点动点从点出发,以每秒个单位长度的速度沿边向终点运动,同时动点从点出发,以每秒个单位长度的速度沿边向终点运动,当点与点、不重合时,以、为邻边作▱ , 设点的运动时间为秒 .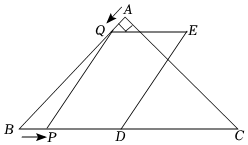 (1)、用含的代数式表示线段的长;(2)、当线段被边平分时,求的值;(3)、设▱的面积为 , 求与之间的函数关系式,并求出时的值.26. 如图,抛物线与轴交于、两点点在点的左侧 , 点的坐标为 , 与轴交于点 , 作直线动点在轴上运动,过点作轴,交抛物线于点 , 交直线于点 , 设点的横坐标为 .
(1)、用含的代数式表示线段的长;(2)、当线段被边平分时,求的值;(3)、设▱的面积为 , 求与之间的函数关系式,并求出时的值.26. 如图,抛物线与轴交于、两点点在点的左侧 , 点的坐标为 , 与轴交于点 , 作直线动点在轴上运动,过点作轴,交抛物线于点 , 交直线于点 , 设点的横坐标为 .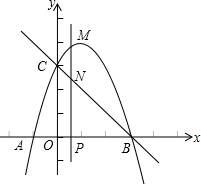 (1)、求抛物线的解析式和直线的解析式;(2)、当点在线段上运动时,求线段的最大值;(3)、当点在线段上运动时,若是以为腰的等腰直角三角形时,求的值;(4)、当以、、、为顶点的四边形是平行四边形时,直接写出的值.
(1)、求抛物线的解析式和直线的解析式;(2)、当点在线段上运动时,求线段的最大值;(3)、当点在线段上运动时,若是以为腰的等腰直角三角形时,求的值;(4)、当以、、、为顶点的四边形是平行四边形时,直接写出的值.