吉林省白山十六中、吉林五中2023-2024学年九年级上学期数学期末考试试卷
试卷更新日期:2024-04-03 类型:期末考试
一、选择题:本题共6小题,每小题2分,共12分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 下列图案中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列事件是随机事件的是( )A、长为 , , 的三条线段能围成一个三角形 B、射击运动员射击一次,命中靶心
2. 下列事件是随机事件的是( )A、长为 , , 的三条线段能围成一个三角形 B、射击运动员射击一次,命中靶心
C、平面内两直线相交,对顶角相等 D、直角三角形的两个锐角互余3. 下列各项中,是的反比例函数的是( )A、 B、 C、 D、4. 某农家前年水蜜桃亩产量为千克,今年的亩产量为千克,设从前年到今年的年平均增长率为 , 则可列方程( )A、 B、 C、 D、5. 如图,线段是的直径,是的弦,过点作的切线交的延长线于点 , , 则 ( ) A、 B、 C、 D、6. 如图 , 某建筑物的屋顶设计成横截面为抛物线形曲线的薄壳屋顶已知它的拱宽为米,拱高为米为了画出符合要求的模板,通常要先建立适当的平面直角坐标系求解析式图是以所在的直线为轴,所在的直线为轴建立的平面直角坐标系,则图中的抛物线的解析式为( )
A、 B、 C、 D、6. 如图 , 某建筑物的屋顶设计成横截面为抛物线形曲线的薄壳屋顶已知它的拱宽为米,拱高为米为了画出符合要求的模板,通常要先建立适当的平面直角坐标系求解析式图是以所在的直线为轴,所在的直线为轴建立的平面直角坐标系,则图中的抛物线的解析式为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题共8小题,每小题3分,共24分。
-
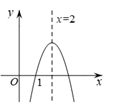
7. 一元二次方程的根的判别式的值是 .8. 若反比例函数的图象分布在第一、三象限,则的取值范围是 .9. 如图,在平面直角坐标系 中,抛物线 的对称轴为直线 ,与x轴的一个交点为 ,则关于x的方程 的解为 .
 10. 在一个不透明的布袋中装有个红球和若干个白球,除颜色外其他都相同,小华通过多次摸球试验后发现,摸到红球的频率稳定在左右,则布袋中白球可能有 个11. 如图,在平面直角坐标系中,直线与双曲线交于、两点,则关于的不等式的解集为 .
10. 在一个不透明的布袋中装有个红球和若干个白球,除颜色外其他都相同,小华通过多次摸球试验后发现,摸到红球的频率稳定在左右,则布袋中白球可能有 个11. 如图,在平面直角坐标系中,直线与双曲线交于、两点,则关于的不等式的解集为 . 12. 如图,是的直径,是的弦, , 垂足为点 , , , 则 .
12. 如图,是的直径,是的弦, , 垂足为点 , , , 则 . 13. 如图,将绕点逆时针旋转得到 , , 若 , , 则旋转角 度
13. 如图,将绕点逆时针旋转得到 , , 若 , , 则旋转角 度 14. 如图是明清时期女子主要裙式之一的马面裙,图马面裙可以近似地看作扇环,其中的长度为米,的长度为米,圆心角 , 则裙长为 米
14. 如图是明清时期女子主要裙式之一的马面裙,图马面裙可以近似地看作扇环,其中的长度为米,的长度为米,圆心角 , 则裙长为 米
三、解答题:本题共12小题,共84分。解答应写出文字说明,证明过程或演算步骤。
-
15. 解方程:x2-2x-4=0.16. 已知抛物线:是常数,且 .(1)、若抛物线在其对称轴左侧的部分是上升的,求的取值范围;
(2)、若抛物线有最低点,且与抛物线的形状相同,求的值.17. 如图,点是反比例函数的图象上的一点,过点作轴于点 , 连接 , 的面积为 . (1)、求反比例函数的解析式;
(1)、求反比例函数的解析式;
(2)、若 , 点是反比例函数上的点,当时,直接写出点的坐标.18. 有张卡片,正面分别印有“祖”用字母代替、“国”用字母代替、“强”用字母代替的字样,卡片的形状、大小、质地等都相同,放在一个不透明的盒子中,将卡片洗匀先从盒子中随机取出一张卡片,记录后不放回,再从剩余的卡片中随机取出一张卡片,请用画树状图或列表的方法,求取出的两张卡片恰好组成“祖国”的概率.19. 若一个角的补角比它的余角的倍还多 , 则这个角的度数为多少度?20. 先化简,再求值: , 其中 .21. 如图,抛物线与轴交于点、 , 是抛物线的顶点,▱的顶点在轴上. (1)、求的值;(2)、若抛物线沿其对称轴向上平移后恰好经过点 , 求平移后抛物线的解析式.22. 如图,是的直径,为上一点,连接 , 作交于点 , 点在的延长线上,经过点 , 且 .
(1)、求的值;(2)、若抛物线沿其对称轴向上平移后恰好经过点 , 求平移后抛物线的解析式.22. 如图,是的直径,为上一点,连接 , 作交于点 , 点在的延长线上,经过点 , 且 . (1)、求证:是的切线;
(1)、求证:是的切线;
(2)、若 , 的半径为 , 求阴影部分的面积.23. 如图,平行四边形的顶点在轴正半轴上, , 反比例函数在第一象限的图象经过点 , 交于点 , 点坐标为 .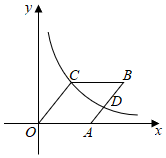 (1)、求的值和点的坐标;
(1)、求的值和点的坐标;
(2)、若是的中点,求的长.24.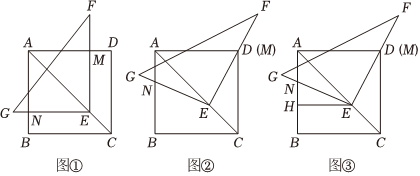 (1)、【知识探究】如图 , 点是正方形的对角线上的一点,以点为直角顶点的的两边、分别与、相交于点、当时,请直接写出与的数量关系 不需证明;
(1)、【知识探究】如图 , 点是正方形的对角线上的一点,以点为直角顶点的的两边、分别与、相交于点、当时,请直接写出与的数量关系 不需证明;
(2)、【拓展探究】当绕点顺时针旋转到点与点重合时,如图 , 请探究与的数量关系,并说明理由;
(3)、【迁移运用】在图的基础上,过点作于点 , 如图 , 求证:是线段的中点.25. 如图,在中, , , , 是的中线,动点从点出发,沿以每秒个单位长度的速度向终点运动,同时,动点从点出发,沿以每秒个单位长度的速度向终点运动,过点作于点 , 连接 , 设四边形与重叠部分图形的面积为 , 点的运动时间为秒 .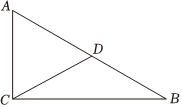 (1)、的长为 用含的代数式表示;(2)、四边形的形状是 不需证明;(3)、求与之间的函数关系式;(4)、当的值为时,直接写出的值.26. 抛物线与轴交于点和 , 与轴交于点 , 连接点是线段下方抛物线上的一个动点不与点 , 重合 , 过点作轴的平行线交于 , 交轴于 , 设点的横坐标为 .
(1)、的长为 用含的代数式表示;(2)、四边形的形状是 不需证明;(3)、求与之间的函数关系式;(4)、当的值为时,直接写出的值.26. 抛物线与轴交于点和 , 与轴交于点 , 连接点是线段下方抛物线上的一个动点不与点 , 重合 , 过点作轴的平行线交于 , 交轴于 , 设点的横坐标为 .
(1)、求该抛物线的解析式;(2)、用关于的代数式表示线段 , 求的最大值及此时点的坐标;(3)、过点作于点 , ,
求点的坐标;
连接 , 在轴上是否存在点 , 使得为直角三角形,若存在,求出点的坐标;若不存在,请说明理由.