吉林省辽源市东辽县2023-2024学年八年级上学期数学期末考试试卷
试卷更新日期:2024-04-03 类型:期末考试
一、选择题:本题共6小题,每小题2分,共12分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 下列图形是化学中常用实验仪器的平面示意图,从左至右分别代表广口瓶、圆底瓶、蒸馏烧瓶和锥形瓶,其中不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是( )A、 B、 C、 D、3. 下列多项式中,能分解因式的是( )A、-a2+b2 B、-a2-b2 C、a2-4a-4 D、a2+ab+b24. 如图,≌ , 点与点 , 点与点是对应顶点连接 , 若 , , 则的度数为( )
2. 下列计算正确的是( )A、 B、 C、 D、3. 下列多项式中,能分解因式的是( )A、-a2+b2 B、-a2-b2 C、a2-4a-4 D、a2+ab+b24. 如图,≌ , 点与点 , 点与点是对应顶点连接 , 若 , , 则的度数为( ) A、 B、 C、 D、5. 如图,在中,平分 , 平分 , 与交于点 , 其中 , 则的度数为( )
A、 B、 C、 D、5. 如图,在中,平分 , 平分 , 与交于点 , 其中 , 则的度数为( )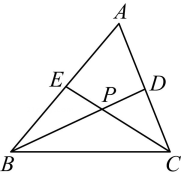 A、 B、 C、 D、6. 如图,在中, , 于点 , 于点 , 于点 , , 则( )
A、 B、 C、 D、6. 如图,在中, , 于点 , 于点 , 于点 , , 则( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题共8小题,每小题3分,共24分。
-
7. 当 时,分式有意义.8. 若一个正多边形的一个内角是 , 则这个正多边形是正边形.9. 若单项式与是同类项,则这两个单项式的积是 .10. 已知 , 则的值为 .11. 如图,BD是∠ABC的角平分线,AD⊥BD,垂足为D,∠DAC=20°,∠C=38°,则∠BAD=.
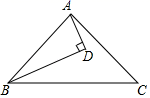 12. 如图,≌ , 点与点 , 点与点为对应顶点,交于点 , 若 , , 则
12. 如图,≌ , 点与点 , 点与点为对应顶点,交于点 , 若 , , 则 13. 如图,点 , 在数轴上,它们所表示的数分别是 , , 且点到原点的距离是点到原点的距离的倍,则 .
13. 如图,点 , 在数轴上,它们所表示的数分别是 , , 且点到原点的距离是点到原点的距离的倍,则 . 14. 数学家斐波那契编写的算经中有如下问题,一组人平分元钱,每人分得若干,若再加上人,平分元钱,则第二次每人所得与第一次相同,求第二次分钱的人数设第二次分钱的人数为 , 则可列方程为 .
14. 数学家斐波那契编写的算经中有如下问题,一组人平分元钱,每人分得若干,若再加上人,平分元钱,则第二次每人所得与第一次相同,求第二次分钱的人数设第二次分钱的人数为 , 则可列方程为 .三、解答题:本题共12小题,共84分。解答应写出文字说明,证明过程或演算步骤。
-
15. 计算: .16. 计算:17. 长春轨道交通号线是长春市正在修建的一条地铁线路,其中末段线路的施工单位计划入冬前盾构施工米,为了尽快完成任务,实际工作效率是原计划工作效率的倍,结果提前天完成盾构施工任务问原计划每天盾构施工多少米?18. 如图,在中, , , 求的度数.
 19. 先化简,再求值: , 其中 , .20. 如图,在的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,如图三个图中的三角形为格点三角形,在图中分别画出与已知三角形成轴对称对称轴不相同的格点三角形.
19. 先化简,再求值: , 其中 , .20. 如图,在的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,如图三个图中的三角形为格点三角形,在图中分别画出与已知三角形成轴对称对称轴不相同的格点三角形. 21. 如图,在中, , , 平分交于点 , 过点作 , 交的延长线于点 .
21. 如图,在中, , , 平分交于点 , 过点作 , 交的延长线于点 . (1)、求的度数;
(1)、求的度数;
(2)、求证:是等腰三角形.22. 如图,在中,是延长线上一点,满足 , 过点作 , 且 , 连接并延长,分别交 , 于点 , . (1)、求证:≌;
(1)、求证:≌;
(2)、若 , , 求的长度.23. 如图,在等边三角形中,D是上的一点,E是延长线上一点,连接、 , 已知 . (1)、求证:是等腰三角形(2)、当 , 时,求的面积.24. 已知分式(1)、化简这个分式
(1)、求证:是等腰三角形(2)、当 , 时,求的面积.24. 已知分式(1)、化简这个分式
(2)、把分式化简结果的分子与分母同时加上后得到分式,问:当时,分式的值较原来分式的值是变大了还是变小了?试说明理由.
(3)、若的值是整数,且也为整数,求出所有符合条件的值25. 先阅读下列材料:我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法,其实分解因式的方法还有分组分解法、拆项法、十字相乘法等等.
分组分解法:将一个多项式适当分组后,可提公因式或运用公式继续分解的方法如:
拆项法:将一个多项式的某一项拆成两项后,可提公因式或运用公式继续分解的方法如:
请你仿照以上方法,探索并解决下列问题:(1)、分解因式:;
(2)、分解因式:;
(3)、多项式有最小值吗?如果有,当它取最小值时的值为多少?26. 如图 , 在中, , , 是经过点的直线,于 , 于 . (1)、求证: .
(1)、求证: .
(2)、若将绕点旋转,使与相交于点如图 , 其他条件不变,求证: .
(3)、在的情况下,若的延长线过的中点如图 , 连接 , 求证: .