四川省绵阳市游仙区2023-2024学年七年级上学期数学期末考试试卷

试卷更新日期：2024-04-03 类型：期末考试

进入出卷网下载

一、单选题

1. 将一张长方形的纸对折，如图，对折1次可得到1条折痕（图中虚线），连续对折3次（对折时每次折痕与上次折痕保持平行），可以得到7条折痕；那么连续对折5次后，可以得到的折痕的条数是（）

A、31条 B、32条 C、33条 D、34条

查看试题解析
2. 下列方程中，是一元一次方程的是（　　）

A、2y－3x ＝5 B、y－3＝5y＋1 C、 $\frac{1}{2}$ x－ 3＝ $\frac{2}{x}$ D、y²－2y ＋3＝0

查看试题解析
3. 如图是一个正方体的展开图，每个面上都有一个汉字，折叠成正方体后，与“负”相对的面上的汉字是（）

A、强 B、课 C、提 D、质

查看试题解析
4. 如果a＝b ，那么下列等式中一定成立的是（　　）

A、a﹣2＝b+2 B、2a+2＝2b+2 C、2a﹣2＝b﹣2 D、2a﹣2＝2b+2

查看试题解析
5. 若 $∠ A = 50 °$ ，则 $∠ A$ 的补角为（）

A、 $40 °$ B、 $50 °$ C、 $130 °$ D、 $140 °$

查看试题解析
6. 下列各式中，属于方程的是（）

A、 $6 + (- 2) = 4$ B、 $\frac{2}{5} x - 2$ C、 $7 x > 5$ D、 $2 x - 1 = 5$

查看试题解析
7. 把正整数1至2021按一定规律排列如图，平移表中带阴影的方框，方框中三个数的和可能是（　　）

A、2016 B、2019 C、2021 D、2022

查看试题解析
8. 商店将进价2400元的彩电标价3600元出售，为了吸引顾客进行打折出售，售后核算仍可获利20%，则折扣为（）

A、九折 B、八五折 C、八折 D、七五折

查看试题解析
9. 若x=3是方程ax+2x=14﹣a的解，则a的值为（）

A、10 B、5 C、4 D、2

查看试题解析
10. 某校学生种植一批树苗，如果每人种10棵，则剩下6棵树苗未种；如果每人种12棵，则缺6棵树苗，若设参与种树的有 $x$ 人，则可列方程为（）

A、 $10 x - 6 = 12 x + 6$ B、 $10 x + 6 = 12 x - 6$ C、 $10 x + 6 = 12 x + 6$ D、 $10 x - 6 = 12 x - 6$

查看试题解析
11. 《九章算术》中有这样一道数学问题，原文如下：清明游园，共坐八船，大船满六，小船满四，三十八学子，满船坐观．请问客家，大小几船？其大意为：清明时节出去游园，所有人共坐了8只船，大船每只坐6人，小船每只坐4人， $38$ 人刚好坐满，问：大、小船各有几只？若设有x只大船，则可列方程为（）

A、 $6 x + 4 x = 38$ B、 $6 (8 - x) + 4 x = 38$ C、 $6 x + 4 (8 - x) = 38$ D、 $8 x + 6 x = 38$

查看试题解析
12. 将一副直角三角板（ $∠ A C B = 30 ° ， ∠ E = 45 °$ ）按如图所示的方式摆放，其中顶点C与顶点F重合，则 $∠ 1$ 的大小为（）

A、 $100 °$ B、 $105 °$ C、 $110 °$ D、 $120 °$

查看试题解析

二、填空题

13. 若 $∠ A = 37 ° 1 2^{'}$ ，则 $∠ A$ 的余角度数是．

查看试题解析
14. 如果 $\frac{x}{x - y}$ ＝ $\frac{3}{2}$ ，那么 $\frac{x}{y}$ 的值等于．

查看试题解析
15. $1 - 2 a + a^{2} = -$ () $= 1 +$ ( )．

查看试题解析
16. 如果线段AB＝5cm，BC＝3cm，且A，B，C三点在同一条直线上，那么A，C两点之间的距离是.

查看试题解析
17. 如果x＝3是方程x＋a＝2的解，则a的值是．

查看试题解析
18. 如图，在数轴上，点A，点B表示的数分别是﹣10，12．点P以2个单位/秒的速度从A出发沿数轴向右运动，同时点Q以3个单位/秒的速度从点B出发沿数轴在B，A之间往返运动．当点P到达点B时，点Q表示的数是．

查看试题解析

三、解答题

19.

(1)、计算： $- 12 - (- 5) + (- 11) - 18$

(2)、解方程： $\frac{x + 3}{2} - x = \frac{2 x + 1}{3}$

查看试题解析
20. 已知平面上有四个村庄，用四个点A、B、C、D表示．

(1)、连接AB；

(2)、作射线AD；

(3)、作直线BC与射线AD交于点E；

(4)、若要建一供电所M ，向四个村庄供电，要使所用电线最短，则供电所M应建在何处？请画出点M的位置并说明理由．

查看试题解析
21. 计算：

(1)、 $5 a + 3 a - (2 a - a)$ ．

(2)、 $(3 x^{2} - x y - 1) - 2 (x^{2} + x y + 2)$ ．

查看试题解析
22. 已知： $O C$ 是 $∠ A O B$ 内部一条射线， $O M$ 是 $∠ A O C$ 的平分线， $O N$ 是 $∠ B O C$ 的平分线．

(1)、如图①所示，若 $A$ ， $O$ ， $B$ 三点共线，则 $∠ M O N$ 的度数是，此时图中共有对互余的角．

(2)、如图②所示，若 $∠ A O B = 110 °$ ，求 $∠ M O N$ 的度数．

(3)、直接写出 $∠ M O N$ 与 $∠ A O B$ 之间的数量关系．

查看试题解析
23. 用8个形状和大小都相同的小长方形，恰好可以拼成如图1所示的大长方形；若用这8个小长方形拼成如图2所示的正方形，则中间留下一个空的小正方形（阴影部分）．设小长方形的长和宽分别为a和b（ $a > b$ ）．

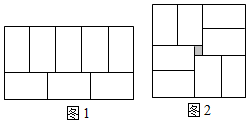(1)、由图1，可知a，b满足的等量关系是；

(2)、若图2中小正方形的边长为3，求小长方形的面积；

(3)、用含b的代数式表示图2中小正方形的面积．

查看试题解析
24. 如图，C是线段AB上一点，AB＝20cm，BC＝8cm，点P从A出发，以2cm/s的速度沿AB向右运动，终点为B；点Q从点B出发，以1cm/s的速度沿BA向左运动，终点为A．已知P、Q同时出发，当其中一点到达终点时，另一点也随之停止运动．设点P运动时间为xs．

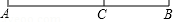(1)、AC＝cm；

(2)、当x＝s时，P、Q重合；

(3)、是否存在某一时刻，使得C、P、Q这三个点中，有一个点恰为另外两点所连线段的中点？若存在，求出所有满足条件的x的值；若不存在，请说明理由．

查看试题解析
25. 数轴上点A表示的数为10，点M，N分别以每秒a个单位长度，每秒b个单位长度的速度沿数轴运动，a， b满足|a-5|+（b-6）²=0.

(1)、请直接与出a= ， b= ；

(2)、如图1，点M从A出发沿数轴向左运动，到达原点后立即返回向右运动：同时点N从原点0出发沿数轴向左运动，运动时间为t，点P为线段ON的中点若MP=MA，求t的值：

(3)、如图2，若点M从原点向右运动，同时点N从原点向左运动，运动时间为t时M运动到点A的右侧，若此时以M，N， O， A为端点的所有线段的长度和为142，求此时点M对应的数.

查看试题解析