四川省成都市简阳市2023-2024学年九年级上学期数学期末考试试卷

试卷更新日期：2024-04-03 类型：期末考试

进入出卷网下载

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求，答案涂在答题卡上）

1. 已知 $\frac{a}{b} = \frac{1}{2}$ ，则下列结论一定正确的是（）

A、 $a = 1$ ， $b = 2$ B、 $a = 2 b$ C、 $b = 2 a$ D、 $b - a = 1$

查看试题解析
2. 如图所示几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 若四条线段 $a$ ， $b$ ， $c$ ， $d$ 成比例，其中 $b = 2 c m$ ， $c = 3 c m$ ， $d = 6 c m$ ，则线段 $a$ 的长为（）

A、 $1 c m$ B、 $2 c m$ C、 $3 c m$ D、 $12 c m$

查看试题解析
4. 如图，已知 $△ A B C ∽ △ D A C$ ， $∠ B = 37 °$ ， $∠ D = 116 °$ ，则 $∠ B A D$ 的度数为（）

A、 $37 °$ B、 $116 °$ C、 $153 °$ D、 $143 °$

查看试题解析
5. 下列命题是假命题的是（）

A、有一组邻边相等的矩形是正方形 B、对角线互相垂直的平行四边形是正方形 C、对角线相等的平行四边形是矩形 D、有三个角是直角的四边形是矩形

查看试题解析
6. 袋中装有6个黑球和一些白球，经过若干次试验，发现“若从中任摸一个球，恰好是白球的概率为 $\frac{1}{3}$ ”，则这个袋中白球大约有（）个．

A、3 B、4 C、5 D、5

查看试题解析
7. 某一芯片实现国产化，经过两次降价，每块芯片单价由118元降为98元，若两次降价的百分率相同，设每次降价的百分率为 $x$ ，根据题意列方程得（）

A、 $118 (1 - x^{2}) = 98$ B、 $118 {(1 - x)}^{2} = 98$ C、 $118 (1 - 2 x) = 98$ D、 $98 {(1 + x)}^{2} = 118$

查看试题解析
8. 如图，正方形 $A B C D$ 的边长为6，点 $E$ 是对角线 $A C$ 上一点，且 $A E = 2 C E$ ，则 $E D$ 的长度为（）

A、4 B、 $2 \sqrt{2}$ C、 $2 \sqrt{3}$ D、 $2 \sqrt{5}$

查看试题解析

二、填空题（本大题共5个小题，每小题4分，共20分，答案写在答题卡上）

9. 若关于 $x$ 的一元二次方程 $x^{2} + 2 m x + m^{2} - m + 3 = 0$ 有实数根，则 $m$ 的取值范围是．

查看试题解析
10. 菱形 $A B C D$ 的周长为 $40 c m$ ，它的一条对角线长 $16 c m$ ，则另一条对角线的长为 $c m$ ．

查看试题解析
11. 已知点 $(2 ， y_{1})$ ， $(1 ， y_{2})$ ， $(- 1 ， y_{3})$ 都在反比例函数 $y = \frac{1}{x}$ 的图象上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ ，的大小关系用“＜”表示为．

查看试题解析
12. 如图所示，要使得 $△ A B C ∽ △ A C D$ ，需要补充的一个条件可以是（只需要填写一个即可）。

查看试题解析
13. 如图，在 $▱ A B C D$ 中，点 $E$ 是 $A D$ 中点，连接 $B E$ ，交 $A C$ 于点 $F$ ，如果 $△ A E F$ 的面积为 $\frac{1}{2}$ ，则四边形 $D C F E$ 的面积为．

查看试题解析

三、解答题（本大题共5个小题，共48分，解答过程写在答题卡上）

14. 解方程

(1)、 $2 x^{2} + 3 x = 0$ ；

(2)、 $x^{2} - 4 x - 5 = 0$ ；

(3)、 $3 x^{2} - 6 x - 1 = 0$ ．

查看试题解析
15. 为了提高学生的综合素养，某校开设了五门手工活动课．按照类别分为： $A$ “剪纸”、 $B$ “沙画”， $C$ “葫芦雕刻”， $D$ “泥塑”， $E$ “插花”．为了了解学生对每种活动课的喜爱情况，随机抽取了部分同学进行调查，将调查结果绘制成如下两幅不完整的统计图．
根据以上信息，回答下列问题：

(1)、本次调查的样本容量为；统计图中的 $a =$ ， $b =$ ．

(2)、通过计算补全条形统计图．若该校共有2500名学生，请你估计全校喜爱“葫芦雕刻”的学生人数；

(3)、剪纸比较优秀的是 $A_{1}$ ， $A_{2}$ 两名女生和 $B_{1}$ 男生三名同学，若从比较优秀的3名同学中随机选取两名同学，参加市举办的剪纸比赛，请利用列表法或树状图法，求恰好选到一名男生和一名女生的概率．

查看试题解析
16. “周末好去处，鳌山公园行”，鳌山公园的印鳌阁塔已成为市民常去的景点．某中学数学组进行综合实践活动，测量印鳌阁塔 $C D$ 的高度．小彤同学在她与印鳌阁塔之间的地面上平放一面镜子，在镜子上做一个标记 $E$ ，她看着镜子来回移动，直至看到印鳌阁塔顶端在镜子中的像与镜子上的标记重合．如图，此时测得 $A B = 1.7 m$ ， $B E = 1 m$ ， $D E = 25 m$ ，求印鳌阁塔 $C D$ 的高度．

查看试题解析
17. 如图， $▱ A B C D$ 中，过点 $C$ 作 $C F ⊥ C D$ ， $C F$ 交 $D B$ 的延长线点 $F$ ；过点 $C$ 作 $C E ∥ D B$ ，交 $A B$ 的延长线于点 $E$ ， $B E$ 交 $C F$ 于点 $O$ ，连接 $E F$ ， $A B = 2 B O = 4$ ．

(1)、求 $O E$ 的长；

(2)、求证：四边形 $B C E F$ 为正方形．

查看试题解析
18. 如图，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象与直线 $y = 4 x$ 交于点 $D (1 ， m)$ ，在射线 $O D$ 上取一点 $A$ ，过点 $A$ 作 $y$ 轴的垂线分别交反比例函数的图象和 $y$ 轴于点 $B$ 和点 $C$ ．

(1)、求反比例函数的解析式；

(2)、当 $A D = 2 O D$ 时，
①求点 $A$ 的坐标；
②求 $△ O B D$ 的面积．

查看试题解析

四、填空题（本大题共5个小题，每小题4分，共20分，答案写在答题卡上）

19. 已知 $y = (1 - m) x^{m^{2} - 2}$ 是反比例函数，则 $m =$ ．

查看试题解析
20. 已知方程 $2 x^{2} + k x + k - 12 = 0$ 的两根之和等于两根之积，则方程两根的平方和为．

查看试题解析
21.
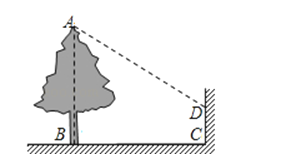
如图，当太阳光与地面上的树影成45°角时，树影投射在墙上的影高CD等于2米，若树根到墙的距离BC等于8米，则树高AB等于米．

查看试题解析
22. 如图，在平面直角坐标系中，矩形 $A B C D$ 对角线的交点为坐标原点 $O$ ，点 $B (m ， 2 m)$ 、 $D$ 在反比例函数 $y = \frac{2}{x}$ 的图象上，点 $A$ 、 $C$ 在 $x$ 轴上，则矩形 $A B C D$ 的面积为．

查看试题解析
23. 如图1，有一张矩形纸片 $A B C D$ ，已知 $A B = 10$ ， $A D = 12$ ，现将纸片进行如下操作：现将纸片沿折痕 $B F$ 进行折叠，使点 $A$ 落在 $B C$ 边上的点 $E$ 处，点 $F$ 在 $A D$ 上（如图2），则 $D F =$ ；然后将 $△ F B E$ 绕点 $F$ 旋转到 $△ F M N$ ，当 $M N$ 过点 $C$ 时旋转停止，则 $E N$ 的长度为．

查看试题解析

五、解答题（本大题共3个小题，共30分，解答过程写在答题卡上）

24. 成都第31届世界大学生夏季运动会（以下简称“成都大运会”）已在今年7月28日到8月8日在成都举行．某商家购进一批成都大运会吉祥物“蓉宝”小挂件，进价为20元/件，调查发现，日销售量 $y$ （单位：件）与售价 $x$ （单位：元/件，且 $20 \leq x \leq 60$ ）之间满足一次函数关系，其部分数据如下表：
$x$ （元/件）
…
30
35
40
…
$y$ （件）
…
60
50
40
…

(1)、求 $y$ 与 $x$ 的函数关系式；

(2)、试问当售价为多少时，使得日销售利润为600元．

查看试题解析
25. 如图，在平面直角坐标系中，直线 $y = \frac{3}{2} x$ 与双曲线 $y = \frac{k}{x} (k > 0)$ 交于点 $A (a ， 3)$ ，点 $B$ ．在双曲线上有一点 $P$ （ $P$ 点在直线 $A B$ 的下方），连接 $P A$ 并延长交 $y$ 轴于点 $C$ ，连接 $B P$ 交 $x$ 轴于点 $Q$ ．

(1)、求点 $A$ 的坐标和 $k$ 的值；

(2)、若 $A P = A C$ ，连接 $B C$ ，求 $△ P B C$ 的面积．

(3)、若 $△ B O Q$ 的面积与四边形 $A O Q P$ 的面积比为 $2 ： 3$ ，求 $P$ 点的坐标；

查看试题解析
26. 在矩形 $A B C D$ 中， $A B ： A D = m ： n$ ，点 $H$ 在边 $D C$ 上（不与点 $C$ ， $D$ 重合），连接 $B H$ ，过点 $C$ 作 $C F ⊥ B H$ 于点 $G$ ．

(1)、当 $m ： n = 3 ： 2$ 时，求 $\frac{B H}{C F}$ ；

(2)、当 $m ： n = 1$ 时，延长 $B H$ 与 $A D$ 交于点 $P$ ，延长 $C F$ 与 $B A$ 交于点 $E$ ，连接 $P E$ ．
①求证： $A E = D P$ ；
②判定 $B F$ 与 $A H$ 的位置关系，并说明理由．

查看试题解析

$x$ （元/件）	…	30	35	40	…
$y$ （件）	…	60	50	40	…