湘教版数学九年级下学期 第1章 二次函数 单元测试B卷
试卷更新日期:2024-04-03 类型:单元试卷
一、选择题
-
1. 在平面直角坐标系中,横坐标和纵坐标都是整数的点叫做整点,已知直线与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,则的取值范围是( )A、 B、 C、 D、且2. 已知抛物线经过和 , 则抛物线的最低点的坐标为( )A、 B、 C、 D、3. 已知二次函数 , 当时,函数有最小值 , 则b的值为( )A、或 B、或 C、 D、或4. 已知反比例函数的图象如图所示,则二次函数的图象大致为( )
 A、
A、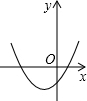 B、
B、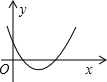 C、
C、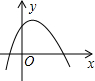 D、
D、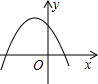 5. 如图所示的是二次函数的部分图象,由图象可知不等式的解集是( )
5. 如图所示的是二次函数的部分图象,由图象可知不等式的解集是( ) A、 B、 C、且 D、或6. 将抛物线 通过一次平移可得到抛物线 .对这一平移过程描述正确的是( )A、向右平移3个单位长度 B、向上平移3个单位长度 C、向左平移3个单位长度 D、向下平移3个单位长度7. 如图,已知开口向上的抛物线与轴交于点 , 对称轴为直线 . 下列结论:①;②;③若关于的方程一定有两个不相等的实数根;④.其中正确的个数有( )
A、 B、 C、且 D、或6. 将抛物线 通过一次平移可得到抛物线 .对这一平移过程描述正确的是( )A、向右平移3个单位长度 B、向上平移3个单位长度 C、向左平移3个单位长度 D、向下平移3个单位长度7. 如图,已知开口向上的抛物线与轴交于点 , 对称轴为直线 . 下列结论:①;②;③若关于的方程一定有两个不相等的实数根;④.其中正确的个数有( )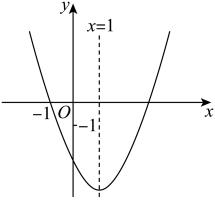 A、1个 B、2个 C、3个 D、4个8. 已知二次函数的对称轴为 , 当时,y的取值范围是 . 则的值为( )A、或 B、或 C、 D、9. 定义:在平面直角坐标系中,若点A满足横、纵坐标都为整数,则把点A叫做“整点”.如:B(3,0)、C(﹣1,3)都是“整点”.抛物线y=ax2﹣2ax+a+2(a<0)与x轴交于点M,N两点,若该抛物线在M、N之间的部分与线段MN所围的区域(包括边界)恰有5个整点,则a的取值范围是( )A、﹣1≤a<0 B、﹣2≤a<﹣1 C、﹣1≤a< D、﹣2≤a<010. 如图1,一个移动喷灌架喷射出的水流可以近似地看成抛物线.图2是喷灌架为一坡地草坪喷水的平面示意图,喷水头的高度(喷水头距喷灌架底部的距离)是1米.当喷射出的水流距离喷水头20米时,达到最大高度11米,现将喷灌架置于坡度为1∶10的坡地底部点O处,草坡上距离О的水平距离为30米处有一棵高度约为2.3米的石榴树AB,因为刚刚被喷洒了农药,近期不能被喷灌.下列说法正确的是( )
A、1个 B、2个 C、3个 D、4个8. 已知二次函数的对称轴为 , 当时,y的取值范围是 . 则的值为( )A、或 B、或 C、 D、9. 定义:在平面直角坐标系中,若点A满足横、纵坐标都为整数,则把点A叫做“整点”.如:B(3,0)、C(﹣1,3)都是“整点”.抛物线y=ax2﹣2ax+a+2(a<0)与x轴交于点M,N两点,若该抛物线在M、N之间的部分与线段MN所围的区域(包括边界)恰有5个整点,则a的取值范围是( )A、﹣1≤a<0 B、﹣2≤a<﹣1 C、﹣1≤a< D、﹣2≤a<010. 如图1,一个移动喷灌架喷射出的水流可以近似地看成抛物线.图2是喷灌架为一坡地草坪喷水的平面示意图,喷水头的高度(喷水头距喷灌架底部的距离)是1米.当喷射出的水流距离喷水头20米时,达到最大高度11米,现将喷灌架置于坡度为1∶10的坡地底部点O处,草坡上距离О的水平距离为30米处有一棵高度约为2.3米的石榴树AB,因为刚刚被喷洒了农药,近期不能被喷灌.下列说法正确的是( ) A、水流运行轨迹满足函数 B、水流喷射的最远水平距离是40米 C、喷射出的水流与坡面OA之间的最大铅直高度是9.1米 D、若将喷灌架向后移动7米,可以避开对这棵石榴树的喷灌
A、水流运行轨迹满足函数 B、水流喷射的最远水平距离是40米 C、喷射出的水流与坡面OA之间的最大铅直高度是9.1米 D、若将喷灌架向后移动7米,可以避开对这棵石榴树的喷灌二、填空题
-
11. 已知二次函数的图像经过原点,那么m的值为 .12. 已知点A(x1 , y1),B(x2 , y2)在抛物线y=x2﹣3上,且0<x1<x2 , 则y1y2.(填“<”或“>”或“=”)13. 关于的二次函数 , 在时有最大值6,则 .14. 如图,抛物线与x轴交于A、B两点,与y轴交于C点,P为抛物线对称轴上动点,则取最小值时,点P坐标是 .
 15. 如图,函数经过点 , 对称轴为直线:①;②;③;④;⑤若点、在抛物线上,则;⑥(为任意实数),其中结论正确的有 .
15. 如图,函数经过点 , 对称轴为直线:①;②;③;④;⑤若点、在抛物线上,则;⑥(为任意实数),其中结论正确的有 .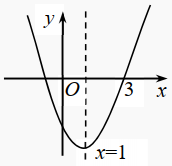
三、解答题
-
16. 已知二次函数的解析式为 .(1)、求证:该二次函数图象与x轴一定有2个交点;(2)、若 , 点 , 都在该二次函数的图象上,且 , 求n的取值范围;(3)、当时,函数最大值与最小值的差为8,求m的值.17. 某智能机器人生产厂家准备对甲、乙两款机器人进行投资生产,根据前期市场调研情况发现,投资甲机器人一年后的收益(万元)与投入成本x()(万元)的函数表达式为: , 投资乙机器人一年后的收益(万元)与投入成本x()(万元)的函数表达式为:.
 (1)、若将2万元资金投给乙机器人,一年后获得的收益是多少?(2)、请在平面直角坐标系中画出两函数图象的简图,并结合图象分析怎样选择投资对象使获得的收益更多?(3)、若该生产厂家共有活动资金32万元,计划全部投入到甲、乙两款机器人生产中,当甲、乙两款机器人分别投入多少万元时,一年后获得的收益之和最大?最大值是多少万元?18. 如图1,抛物线y=﹣x2+bx+c过点A(﹣1,0),点B(3,0),与y轴交于点C . 在x轴上有一动点E(m , 0)(0<m<3),过点E作直线ME⊥x轴,交抛物线于点M .
(1)、若将2万元资金投给乙机器人,一年后获得的收益是多少?(2)、请在平面直角坐标系中画出两函数图象的简图,并结合图象分析怎样选择投资对象使获得的收益更多?(3)、若该生产厂家共有活动资金32万元,计划全部投入到甲、乙两款机器人生产中,当甲、乙两款机器人分别投入多少万元时,一年后获得的收益之和最大?最大值是多少万元?18. 如图1,抛物线y=﹣x2+bx+c过点A(﹣1,0),点B(3,0),与y轴交于点C . 在x轴上有一动点E(m , 0)(0<m<3),过点E作直线ME⊥x轴,交抛物线于点M . (1)、求抛物线的解析式;(2)、当m=1时,点D是直线ME上的点且在第一象限内,若△ACD是以CA为斜边的直角三角形,求点D的坐标;(3)、如图2,连接BC , BC与ME交于点F , 连接AF , △ACF和△BFM的面积分别为S1和S2 , 当S1=4S2时,求点E坐标.
(1)、求抛物线的解析式;(2)、当m=1时,点D是直线ME上的点且在第一象限内,若△ACD是以CA为斜边的直角三角形,求点D的坐标;(3)、如图2,连接BC , BC与ME交于点F , 连接AF , △ACF和△BFM的面积分别为S1和S2 , 当S1=4S2时,求点E坐标.四、实践探究题
-
19. 根据以下素材,探究完成任务
素材1 图1是一个瓷碗,图2是其截面图,碗体DEC呈抛物线状(碗体厚度不计),碗高GF=7cm,碗底宽AB=3cm,当瓷碗中装满面汤时,液面宽CD= 12cm,
此时面汤最大深度EG= 6cm,
素材2 如图3,把瓷碗绕点B缓缓倾斜倒出部分面汤,当点A离MN距离为1.8cm时停止.

问题解决 任务1 确定碗体形状 在图2中建立合适的直角坐标系,求抛物线的函数表达式。
任务2 拟定设计方案1 根据图2位置,把碗中面汤喝掉一部分,当碗中液面高度(离桌面MN距离)为5cm时,求此时碗中液面宽度。
任务3 拟定设计方案2 如图3,当碗停止倾斜时,求此时碗中液面宽度CH。
20.(1)、【问题初探】综合与实践数学活动课上,张老师给出了一个问题:
已知二次函数y=x2+2x-3,当-2≤x≤2时,y的取值范围为;
①小伟同学经过分析后,将原二次函数配方成y=a(x-h)2+k
形式,确定抛物线对称轴为直线x=h , 通过-2、h和2的大小
关系,分别确定了最大值和最小值,进而求出y的取值范围;
②小军同学画出如图的函数图象,通过观察图象确定了y的取值范围;请你根据上述两名同学的分析写出y的取值范围是;
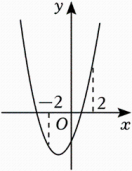 (2)、【类比分析】
(2)、【类比分析】张老师发现两名同学分别从“数”和“形”的角度分析、解决问题,为了让同学们更好感悟“数形结合”思想,张老师将前面问题变式为下面问题,请你解答:已知二次函数y=-x2+2x-3,当-2≤x≤2时,求y的取值范围;
(3)、【学以致用】已知二次函数y=-x2+6x-5,当a≤x≤a+3时,二次函数的最大值为y1 , 最小值为y2 , 若y1-y2=3,求a的值.
21. 根据以下素材,探索完成任务.素材1
某学校一块劳动实践基地大棚的横截面如图所示,上部分的顶棚是抛物线形状,下部分是由两根立柱和组成,立柱高为 , 顶棚最高点距离地面是 , 的长为 .

素材2
为提高灌溉效率,学校在的中点处安装了一款可垂直升降的自动喷灌器 , 从喷水口喷出的水流可以看成抛物线,其形状与的图象相同, , 此时水流刚好喷到立柱的端点处.
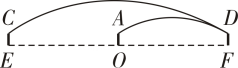
问题解决
任务1
确定顶棚的形状
以顶棚最高点为坐标原点建立平面直角坐标系,求出顶棚部分抛物线的表达式.
任务2
探索喷水的高度
问处喷出的水流在距离点水平距离为多少米时达到最高.
任务3
调整喷头的高度
如何调整喷水口的高度(形状不变),使水流喷灌时恰好落在边缘处.
五、综合题
-
22. 抛物线y=ax2+bx﹣2与x轴交于A、B两点(点A在点B的左侧),且A(﹣1,0),B(4,0),与y轴交于点C . 连结BC , 以BC为边,点O为中心作菱形BDEC , 点P是x轴上的一个动点,设点P的坐标为(m , 0),过点P作x轴的垂线交抛物线于点Q , 交BD于点M .
 (1)、求该抛物线对应的函数表达式;(2)、x轴上是否存在一点P , 使△PBC为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由;(3)、当点P在线段OB上运动时,试探究:当m为何值时,四边形CQMD是平行四边形?请说明理由.23. 如图,抛物线y=-x2+bx+c与x轴相交于A(-1,0),B(5,0)两点.
(1)、求该抛物线对应的函数表达式;(2)、x轴上是否存在一点P , 使△PBC为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由;(3)、当点P在线段OB上运动时,试探究:当m为何值时,四边形CQMD是平行四边形?请说明理由.23. 如图,抛物线y=-x2+bx+c与x轴相交于A(-1,0),B(5,0)两点.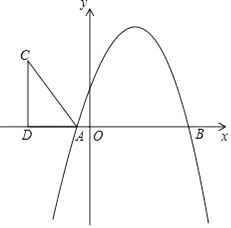 (1)、求抛物线的解析式;(2)、在第二象限内取一点C,作CD垂直x轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;
(1)、求抛物线的解析式;(2)、在第二象限内取一点C,作CD垂直x轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;
(3)、在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请出点Q的坐标;若不存在,请说明理由.
24. 如图,抛物线y=﹣ x2+ x+2与x轴交于点A,B,与y轴交于点C. (1)、试求A,B,C的坐标;(2)、将△ABC绕AB中点M旋转180°,得到△BAD.
(1)、试求A,B,C的坐标;(2)、将△ABC绕AB中点M旋转180°,得到△BAD.①求点D的坐标;
②判断四边形ADBC的形状,并说明理由;
(3)、在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请直接写出所有满足条件的P点的坐标;若不存在,请说明理由.