湘教版数学九年级下学期 第1章 二次函数 单元测试A卷
试卷更新日期:2024-04-03 类型:单元试卷
一、选择题
-
1. 二次函数的图象与x轴的交点个数是( )A、0个 B、1个 C、2个 D、不能确定2. 抛物线的对称轴是( )A、直线 B、直线 C、直线 D、直线3. 顶点 , 且开口方向、形状与函数的图象相同的抛物线的是( )A、 B、 C、 D、4. 二次函数的图象经过点 , 则a的值是( )A、 B、 C、 D、25. 在平面直角坐标系中,将抛物线向上平移2个单位长度,再向右平移1个单位长度,得到的抛物线的解析式是A、 B、 C、 D、6. 设点 , , 是抛物线上的三点,则 , , 的大小关系为( )A、 B、 C、 D、7. 下列函数中是二次函数的是( )A、 B、 C、 D、8. 一次函数与二次函数在同一坐标系内的图象可能为( )A、
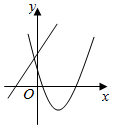 B、
B、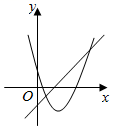 C、
C、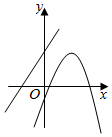 D、
D、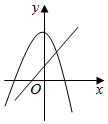 9. 如图是二次函数 , , 是常数,图象的一部分,对称轴为直线 , 经过点 , 且与轴的交点在点与之间.下列判断中,正确的是
9. 如图是二次函数 , , 是常数,图象的一部分,对称轴为直线 , 经过点 , 且与轴的交点在点与之间.下列判断中,正确的是 A、 B、 C、 D、10. 如表中列出了二次函数y=ax2+bx+c(a≠0)的一些对应值,则一元二次方程ax2+bx+c=0(a≠0)的一个近似解x1的范围是( )
A、 B、 C、 D、10. 如表中列出了二次函数y=ax2+bx+c(a≠0)的一些对应值,则一元二次方程ax2+bx+c=0(a≠0)的一个近似解x1的范围是( )x
…
﹣3
﹣2
﹣1
0
1
…
y
…
﹣11
﹣5
﹣1
1
1
…
A、﹣3<x1<﹣2 B、﹣2<x1<﹣1 C、﹣1<x1<0 D、0<x1<1二、填空题
-
11. 二次函数的图象经过点 , 且当时,有最大值 , 则该二次函数解析式为 .12. 二次函数的顶点坐标是13. 已知 , 在二次函数的图象上,比较(填、或14. 如图,在平面直角坐标系中,正方形OABC的顶点A在x轴的正半轴上,顶点C在y轴的正半轴上,抛物线经过点B、C.若抛物线的顶点在正方形OABC的内部,则a的取值范围是.
 15. 如图,抛物线与轴相交于点和点 , 与轴相交于点 , 作直线 . 若在直线上方的抛物线上存在点 , 使 , 则点的坐标为 .
15. 如图,抛物线与轴相交于点和点 , 与轴相交于点 , 作直线 . 若在直线上方的抛物线上存在点 , 使 , 则点的坐标为 .
三、解答题
-
16. 如图1,一个移动喷灌架喷射出的水流可以近似地看成抛物线. 图2是喷灌架为一坡地草坪喷水的平面示意图,喷水头的高度(喷水头距喷灌架底部的距离)是1米,当喷射出的水流与喷灌架的水平距离为10米时,达到最大高度6米,现将喷灌架置于坡地底部点O处,草坡上距离O的水平距离为15 米处有一棵高度为1.2米的小树AB,AB垂直水平地面且A点到水平地面的距离为3米.
 (1)、计算说明小树是否会对水流浇灌到树后面的草坪造成影响?(2)、求水流的高度与斜坡铅垂高度差的最大值.17. 某商场将进货价为30元的台灯以40元售出,平均每月能售出600个,调查表明:售价在40元至60元范围内,这种台灯的售价每上涨1元,其销售量就将减少10个,设该商场决定把售价上涨x(0<x<20,x是整数)元.(1)、售价上涨元后,该商场平均每月可售出 个台灯(用含的代数式表示);(2)、为了实现平均每月10000元的销售利润,这种台灯的售价应定为多少元?这时应进台灯多少个?(3)、台灯售价定为多少元时,每月销售利润最大?18. 如图所示,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=(k>0)的图象与BC边交于点E.
(1)、计算说明小树是否会对水流浇灌到树后面的草坪造成影响?(2)、求水流的高度与斜坡铅垂高度差的最大值.17. 某商场将进货价为30元的台灯以40元售出,平均每月能售出600个,调查表明:售价在40元至60元范围内,这种台灯的售价每上涨1元,其销售量就将减少10个,设该商场决定把售价上涨x(0<x<20,x是整数)元.(1)、售价上涨元后,该商场平均每月可售出 个台灯(用含的代数式表示);(2)、为了实现平均每月10000元的销售利润,这种台灯的售价应定为多少元?这时应进台灯多少个?(3)、台灯售价定为多少元时,每月销售利润最大?18. 如图所示,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=(k>0)的图象与BC边交于点E. (1)、当F为AB的中点时,求该反比例函数的解析式;(2)、当k为何值时,△EFA的面积最大,最大面积是多少?
(1)、当F为AB的中点时,求该反比例函数的解析式;(2)、当k为何值时,△EFA的面积最大,最大面积是多少?四、综合题
-
19. 一大型商场经营某种品牌商品,该商品的进价为每件30元,根据市场调查发现,该商品每周的销售量y(件)与售价x(元/件)(x为正整数)之间满足一次函数关系,下表记录的是某三周的有关数据:
x(元/件)
40
50
60
y(件)
10000
9500
9000
(1)、求y与x的函数关系式(不求自变量的取值范围);(2)、在销售过程中要求销售单价不低于成本价,且不高于150元/件.若某一周该商品的销售量不少于6000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?(3)、抗疫期间,该商场这种商品售价不大于150元/件时,每销售一件商品便向某慈善机构捐赠m元(10≤m≤60),捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.请求出m的取值范围.20. 某企业接到一批帽子生产任务,按要求在20天内完成,约定这批帽子的出厂价为每顶8元.为按时完成任务,该企业招收了新工人,设新工人小华第x天生产的帽子数量为y顶,y与x满足如下关系式: (1)、小华第几天生产的帽子数量为220顶?(2)、如图,设第x天每顶帽子的成本是P元,P与x之间的关系可用图中的函数图象来刻画.若小华第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大?最大值是多少元?(3)、设(2)小题中第m天利润达到最大值,若要使第天的利润比第m天的利润至少多49元,则第天每顶帽子至少应提价几元?21. 如图,已知抛物线交x轴于A(-3,0),B(4,0)两点,交y轴于点C,点P是抛物线上一点,连接AC、BC.
(1)、小华第几天生产的帽子数量为220顶?(2)、如图,设第x天每顶帽子的成本是P元,P与x之间的关系可用图中的函数图象来刻画.若小华第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大?最大值是多少元?(3)、设(2)小题中第m天利润达到最大值,若要使第天的利润比第m天的利润至少多49元,则第天每顶帽子至少应提价几元?21. 如图,已知抛物线交x轴于A(-3,0),B(4,0)两点,交y轴于点C,点P是抛物线上一点,连接AC、BC.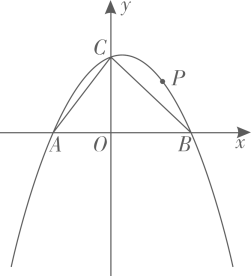 (1)、求抛物线的表达式;(2)、连接OP,BP,若 , 求点P的坐标;(3)、在抛物线的对称轴上是否存在点Q,使得∠QBA=75°?若存在,直接写出点Q的坐标;若不存在,请说明理由.22. [定义]若抛物线与一水平直线交于两点,我们把这两点间线段的长称为抛物线关于这条直线的跨径,抛物线的顶点到该直线的距离称为抛物线关于这条直线的矢高,矢高与跨径的比值称为抛物线关于这条直线的矢跨比.(1)、如图,抛物线y=ax2+bx+c的顶点为P,PC⊥x轴于点C,它与x轴交于点A,B,则AB的长为抛物线y=ax2+bx+c关于x轴的跨径,PC的长为抛物线y=a2+bx+c关于x轴的矢高,的值为抛物线y=ax2+bx+c关于x轴的矢跨比.
(1)、求抛物线的表达式;(2)、连接OP,BP,若 , 求点P的坐标;(3)、在抛物线的对称轴上是否存在点Q,使得∠QBA=75°?若存在,直接写出点Q的坐标;若不存在,请说明理由.22. [定义]若抛物线与一水平直线交于两点,我们把这两点间线段的长称为抛物线关于这条直线的跨径,抛物线的顶点到该直线的距离称为抛物线关于这条直线的矢高,矢高与跨径的比值称为抛物线关于这条直线的矢跨比.(1)、如图,抛物线y=ax2+bx+c的顶点为P,PC⊥x轴于点C,它与x轴交于点A,B,则AB的长为抛物线y=ax2+bx+c关于x轴的跨径,PC的长为抛物线y=a2+bx+c关于x轴的矢高,的值为抛物线y=ax2+bx+c关于x轴的矢跨比. (2)、[特例]如图15,已知抛物线y=-x2+4与x轴交于点C,D (点C在点D右侧):
(2)、[特例]如图15,已知抛物线y=-x2+4与x轴交于点C,D (点C在点D右侧):①抛物线y=-x2+4关于x轴的矢高是 , 跨径是 , 矢跨比是;
②有一抛物线经过点c,与抛物线y=-x2+4开口方向与大小一样,且矢高是抛物线y=-x2+4关于x轴的矢高的 , 求它关于x轴的矢跨比;
 (3)、[推广]结合抛物线的平移规律可以发现,两条开口方向与大小一样的抛物线,若第一条抛物线的矢高是第二条抛物线关于同一直线的矢高的k(k>0)倍,则第一条抛物线的跨径是第二条抛物线关于同一直线的跨径的倍(用含k的代数式表示);(4)、[应用]如图16是某地一座三拱桥梁建筑示意图,其中主跨与边跨的拱轴线为开口方向与大小一样的抛物线,它们关于水平钢梁所在直线的跨径分别为420米与280米,已知主跨的矢跨比为 , 则边跨的矢跨比是。
(3)、[推广]结合抛物线的平移规律可以发现,两条开口方向与大小一样的抛物线,若第一条抛物线的矢高是第二条抛物线关于同一直线的矢高的k(k>0)倍,则第一条抛物线的跨径是第二条抛物线关于同一直线的跨径的倍(用含k的代数式表示);(4)、[应用]如图16是某地一座三拱桥梁建筑示意图,其中主跨与边跨的拱轴线为开口方向与大小一样的抛物线,它们关于水平钢梁所在直线的跨径分别为420米与280米,已知主跨的矢跨比为 , 则边跨的矢跨比是。