湘教版数学八年级下学期 第4章 一次函数 单元测试B卷
试卷更新日期:2024-04-03 类型:单元试卷
一、选择题
-
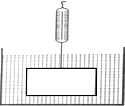
1. 如图,挂在弹簧秤上的长方体铁块浸没在水中,提着弹簧匀速上移,直至铁块浮出水面停留在空中(不计空气阻力),弹簧秤的读数F(kg)与时间t(s)的函数图象大致是( )
 A、
A、 B、
B、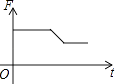 C、
C、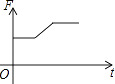 D、
D、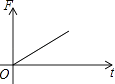 2. 在函数中,自变量的取值范围是( )A、 B、 C、 D、3. 把函数y=x的图象向上平移2个单位,下列各点在平移后的函数图象上的是( )A、(2,2) B、(2,3) C、(2,4) D、(2,5)4. 如图 , 在中, , 点从点出发,以每秒个单位长度的速度沿匀速运动到点 , 图是点运动时,线段的长度随时间变化的图象,则的边长为( )
2. 在函数中,自变量的取值范围是( )A、 B、 C、 D、3. 把函数y=x的图象向上平移2个单位,下列各点在平移后的函数图象上的是( )A、(2,2) B、(2,3) C、(2,4) D、(2,5)4. 如图 , 在中, , 点从点出发,以每秒个单位长度的速度沿匀速运动到点 , 图是点运动时,线段的长度随时间变化的图象,则的边长为( )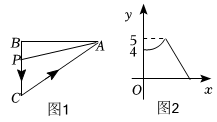 A、 B、 C、 D、5. 对于一次函数y=-2x+4,下列说法错误的是( )A、y随x的增大而减小 B、图象与y轴交点为(0,4) C、图象经过第一、二、四象限 D、图象经过点(1,3)6. 如图是一次函数 ( 、 是常数)的图象,则不等式 的解集是( )
A、 B、 C、 D、5. 对于一次函数y=-2x+4,下列说法错误的是( )A、y随x的增大而减小 B、图象与y轴交点为(0,4) C、图象经过第一、二、四象限 D、图象经过点(1,3)6. 如图是一次函数 ( 、 是常数)的图象,则不等式 的解集是( ) A、 B、 C、 D、7. 如图,一直线与两坐标轴的正半轴分别交于、两点,是线段上任意一点(不包括端点),过点分别作两坐标轴的垂线,与两坐标轴围成的矩形的周长为4,则线段的最小值为( )
A、 B、 C、 D、7. 如图,一直线与两坐标轴的正半轴分别交于、两点,是线段上任意一点(不包括端点),过点分别作两坐标轴的垂线,与两坐标轴围成的矩形的周长为4,则线段的最小值为( ) A、 B、1 C、 D、28. 如图,正方形ABCD对角线的交点刚好在坐标原点,其中点D坐标为(1,1),若将对角线BD绕点B逆时针旋转30°后所在的直线交y轴于点E,连接AE.下列4个结论:
A、 B、1 C、 D、28. 如图,正方形ABCD对角线的交点刚好在坐标原点,其中点D坐标为(1,1),若将对角线BD绕点B逆时针旋转30°后所在的直线交y轴于点E,连接AE.下列4个结论:①点O到直线BE的距离为;②OE的长为;③AB=AE;④直线AE的解析
式为y=x++1.其中正确的是( )
 A、①④ B、②④ C、①②③ D、①③④9. 小明、小宇从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小宇骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s(米)与小明出发时间t(分)之间的函数关系如图所示.下列说法:①小宇先到达青少年宫;②小宇的速度是小明速度的3倍;③a=20;④b=600.其中正确的是( )
A、①④ B、②④ C、①②③ D、①③④9. 小明、小宇从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小宇骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s(米)与小明出发时间t(分)之间的函数关系如图所示.下列说法:①小宇先到达青少年宫;②小宇的速度是小明速度的3倍;③a=20;④b=600.其中正确的是( ) A、①②③ B、①②④ C、①③④ D、①②③④10. 如图,直线 : 与直线 : 相交于点 ,直线 与 轴交于点 ,一动点 从点 出发,先沿平行于 轴
A、①②③ B、①②④ C、①③④ D、①②③④10. 如图,直线 : 与直线 : 相交于点 ,直线 与 轴交于点 ,一动点 从点 出发,先沿平行于 轴 方向运动,到达直线 上的点 处后,改为垂直于 轴的方向运动,到达直线 上的点 处后,再沿平行于 轴的方向运动,到达直线 上的点 处后,又改为垂直于 轴的方向运动,到达直线 上的点 处后,仍沿平行于 轴的方向运动…照此规律运动,动点 依次经过点 , , , , , , , …则 的长度为( )
方向运动,到达直线 上的点 处后,改为垂直于 轴的方向运动,到达直线 上的点 处后,再沿平行于 轴的方向运动,到达直线 上的点 处后,又改为垂直于 轴的方向运动,到达直线 上的点 处后,仍沿平行于 轴的方向运动…照此规律运动,动点 依次经过点 , , , , , , , …则 的长度为( )
 A、 B、 C、2022 D、4044
A、 B、 C、2022 D、4044二、填空题
-
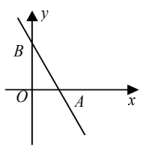
11. 函数y= 中自变量x的取值范围是 .12. 若点A , B在一次函数(m是常数)的图象上,则 , 的大小关系是 . (填“>”,“=”或“<”).13. 在平面直角坐标系中,若反比例函数的图象经过点 , 则一次函数的图象一定不经过第 象限.14. 如图,已知直线与轴交于点 , 与轴交于点 , 把绕点旋转 , 点落在点处,则直线的表达式为 .
 15. 如图,在Rt△ABC中,∠ACB=90°,AC=6,AB=10,点D以每秒5个单位长度的速度从点B处沿沿射线BC方向运动,点F以相同的速度从点A出发沿边AB向点B运动,当F运动至点B时,点D停止运动.设点D运动时间为t秒,以DF为对角线作正方形DEFG,在运动过程中,若正方形DEFG的一边恰好落在Rt△ABC的一边上,则t=.
15. 如图,在Rt△ABC中,∠ACB=90°,AC=6,AB=10,点D以每秒5个单位长度的速度从点B处沿沿射线BC方向运动,点F以相同的速度从点A出发沿边AB向点B运动,当F运动至点B时,点D停止运动.设点D运动时间为t秒,以DF为对角线作正方形DEFG,在运动过程中,若正方形DEFG的一边恰好落在Rt△ABC的一边上,则t=.
三、解答题
-
16. 如图,四边形OABC是矩形,点A,C在坐标轴上,点B坐标为(-1,3),△ODE是△OCB绕点O顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H.
 (1)、求直线BD的表达式.(2)、求点H到x轴的距离.(3)、点M在坐标轴上,平面内是否存在点N,使以点D,F,M,N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.(提示:两直线垂直,斜率乘积为-1)17. 已知y-2与x成正比,且当x=2时,y=-6.(1)、求y与x之间的函数关系式;(2)、若点在这个函数图象上,求a的值.18. 如图,折线是在某市乘出租车所付车费(元)与行车里程之间的函数关系图象.
(1)、求直线BD的表达式.(2)、求点H到x轴的距离.(3)、点M在坐标轴上,平面内是否存在点N,使以点D,F,M,N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.(提示:两直线垂直,斜率乘积为-1)17. 已知y-2与x成正比,且当x=2时,y=-6.(1)、求y与x之间的函数关系式;(2)、若点在这个函数图象上,求a的值.18. 如图,折线是在某市乘出租车所付车费(元)与行车里程之间的函数关系图象. (1)、根据图象,求当时,该图象的函数关系式;(2)、某人乘坐应付多少钱?(3)、若某人付车费30.8元,出租车行驶了多少千米?
(1)、根据图象,求当时,该图象的函数关系式;(2)、某人乘坐应付多少钱?(3)、若某人付车费30.8元,出租车行驶了多少千米?四、实践探究题
-
19. 【学习材料】
求直线向右平移个单位长度后的解析式.
第一步,在直线上任意取两点和;
第二步,将点和向右平移个单位长度得到点和 , 则直线就是直线向右平移个单位长度后得到的直线;
第三步,设直线的解析式为: , 将和代入得到:解得 , 所以直线的解析式为: .
(1)、【类比思考】若将直线向左平移个单位长度,则平移后的直线解析式为 ;
若先将直线向右平移个单位长度,再向下平移个单位长度,得到直线 , 则直线的解析式为 .
(2)、【拓展应用】已知一次函数的图象与直线关于轴对称,求一次函数的解析式;
若一次函数的图象绕点逆时针旋转后得到直线 , 则直线的解析式为 ▲ .
五、综合题
-
20. 在平面直角坐标系中,直线:经过点 , 交轴于点 .(1)、求直线所对应的函数表达式.(2)、若点是轴上一点,连结当的面积为时,求点的坐标.(3)、已知线段的端点坐标分别为、 .
当直线与线段有交点时,求的取值范围.
已知点是直线上一点,其横坐标为过点作直线轴,将直线在直线下方部分记作 , 在直线上及其上方的部分记为 , 将沿直线向上翻折得到 , 和两部分组成的图象记为当图象与线段四有一个公共点时,直接写出的取值范围.
21. 在平面直角坐标系中,已知点 , , 对于直线l和点P , 给出如下定义:若在线段上存在点Q , 使得点P , Q关于直线l对称,则称直线l为点P的关联直线,点P是直线l的关联点. (1)、已知直线: , 在点 , , 中,直线的关联点是;(2)、若在x轴上存在点P , 使得点P为直线:的关联点,求b的取值范围;(3)、已知点 , 若存在直线:是点N的关联直线,直接写出n的取值范围.22. 如图1,一次函数的图象与坐标轴交于点 , , 平分交轴与点 , , 垂足为 .
(1)、已知直线: , 在点 , , 中,直线的关联点是;(2)、若在x轴上存在点P , 使得点P为直线:的关联点,求b的取值范围;(3)、已知点 , 若存在直线:是点N的关联直线,直接写出n的取值范围.22. 如图1,一次函数的图象与坐标轴交于点 , , 平分交轴与点 , , 垂足为 . (1)、求所在直线的解析式;(2)、如图2,点是线段上的一点,点是线段上的一点,求的最小值.(3)、求点 , 的坐标;
(1)、求所在直线的解析式;(2)、如图2,点是线段上的一点,点是线段上的一点,求的最小值.(3)、求点 , 的坐标;
-