2023-2024学年初中数学湘教版八年级下学期第4章一次函数单元测试A卷

试卷更新日期：2024-04-03 类型：单元试卷

进入出卷网下载

一、选择题

1. 函数y＝ $\frac{1}{\sqrt{x - 2}}$ +x-2的自变量x的取值范围是（）

A、x≥2 B、x＞2 C、x≠2 D、x≤2

查看试题解析
2. 如图，把 $R_{1} ， R_{2}$ 两个电阻串联起来，线路 $A B$ 上的电流为 $I$ ，电压为 $U$ ，则 $U = I R_{1} + I R_{2}$ ，当 $R_{1} = 9.7 ， R_{2} = 10.3 ， I = 2$ 时， $U$ 的值是（）

A、 $37$ B、 $38$ C、 $39$ D、 $40$

查看试题解析
3. 已知 $(- 1 ， y_{1})$ ， $(- 0.5 ， y_{2})$ ， $(1.8 ， y_{3})$ 是直线 $y = - 2 x + b$ （b为常数）上的三个点，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{1} > y_{3} > y_{2}$ C、 $y_{3} > y_{1} > y_{2}$ D、 $y_{3} > y_{2} > y_{1}$

查看试题解析
4. 已知一次函数 $y = k x + 2 (k > 0)$ ，则该函数的图象大致是 $($ 　　 $)$

A、 B、 C、 D、

查看试题解析
5. 已知函数 $y = {\begin{array}{l} 2 x - 1 (x \geq 1) \\ - x + 2 (x < 1 ） \end{array}$ ，当 $x = - 1$ 时， $y$ 的值为（　　）

A、 $3$ B、 $- 3$ C、 $1$ D、 $- 1$

查看试题解析
6. 在一定的条件下，若物体运动的路程s（米）与时间t（秒）的关系式为s=5t²+2t，则当t=4秒时，该物体所经过的路程为（）

A、28米 B、48米 C、68米 D、88米

查看试题解析
7. 一次函数y＝2x+m的图象经过两个点A（-1，y₁）和B（2，y₂），则y₁与y₂的大小关系是（）

A、y₁＜y₂ B、y₁＞y₂ C、当m＞0时，y₁＞y₂ D、当m＜0时，y₁＞y₂

查看试题解析
8. 小明和爸爸从家里出发，沿同一路线到图书馆，小明匀速跑步先出发，2分钟后，爸爸骑自行车出发，匀速骑行一段时间后，在途中商店买水花费了5分钟，从商店出来后，爸爸的骑车速度比他之前的骑车速度增加60米/分钟，结果与小明同时到达图书馆．小明和爸爸两人离开家的路程s（米）与小明出发的时间t（分钟）之间的函数图象如图所示，则下列说法错误的是（）

A、a＝17． B、小明的速度是150米/分钟． C、爸爸从家到商店的速度是200米/分钟． D、t＝9时，爸爸追上小明．

查看试题解析
9. 在学习了用描点法画函数图象之后，小马同学对某个一次函数列表取对应值如下：
x
…
-2
-1
0
1
2
…
y
…
-5
-3
-1
0
3
…
他在最后描点连线时发现有一个点明显不对，这个点是（）．

A、 $(- 1 ， - 3)$ B、 $(0 ， - 1)$ C、 $(1 ， 0)$ D、 $(2 ， 3)$

查看试题解析
10. 如图1，在 $R t △ A B C$ 中， $∠ A = 90 °$ ，点 $P$ 从点 $A$ 出发，沿三角形的边 $A C - C B - B A$ 以 $1 c m / s$ 的速度运动，图2是点 $P$ 运动时，线段 $A P$ 的长度 $y (c m)$ 随运动时间 $x (s)$ 变化的图象．若点 $D$ 是曲线的最低点，则点 $D$ 的纵坐标为（）

A、 $\frac{18}{5}$ B、4 C、 $\frac{24}{5}$ D、6

查看试题解析

二、填空题

11. 若一次函数 $y = k x + 2$ 的图象向下平移3个单位长度后经过点 $(2 ， - 5)$ ，则平移后的一次函数表达式是.

查看试题解析
12. 函数y＝ $\sqrt{x-1}$ 的自变量x的取值范围是.

查看试题解析
13. 如图，要围一个长方形ABCD的菜园，菜园的一边利用足够长的墙，用35米长的篱笆围成另外三边．为了方便进出，在BC边上留了一个2米宽的小门．设AB边的长为x米，BC边的长为y米，则y与x之间的关系式是．

查看试题解析
14. 根据如图所示的计算程序计算变量y的值，若输入 $m = 3$ ， $n = 2$ 时，则输出y的值是．

查看试题解析
15. 已知直线 $l_{1} ： y = k x + k + 1$ 与 $l_{2} ： y = (k + 1) x + k + 2$ （其中k为正整数），记 $l_{1} ， l_{2}$ 与x轴围成的三角形面积为 $S_{k}$ ，则 $S_{1} + S_{2} + S_{3} + ⋯ + S_{100} =$ ．

查看试题解析

三、作图题

16. 已知一次函数y＝kx+4，一次函数图象经过点（ $\frac{1}{2}$ ， 3）．

(1)、求这个一次函数的解析式，并画出该函数的图象；

(2)、若该一次函数的图象与x轴交于点A，与y轴交于点B，求△OAB的面积．

(3)、当﹣2≤y＜4时，求自变量x的取值范围．

查看试题解析

四、解答题

17. 已知一次函数 $y = k x + b$ ，它的图象经过 $(1 ， - 3)$ ， $(4 ， 6)$ 两点．

(1)、求y与x之间的函数表达式．

(2)、当 $- 1 \leq x \leq 4$ 时，求函数值y的取值范围．

查看试题解析
18. 双休日，张老师从家出发，骑自行车去南街碳水王国游玩，途中仅在经过大佛城路口时遇到红灯，他本次骑自行车所经过的路程y米与所用时间x分钟的函数图象如图所示，请根据图象提供的信息回答下列问题：

(1)、张老师家到南街碳水王国的路程是米；在大佛城路口遇红灯停留了分钟．

(2)、如果骑车速度超过300米/分钟就存在安全隐患，那么张老师从通过大佛城红绿灯后到南街碳水王国，这段时间的平均速度是否存在安全隐患？请说明理由．

查看试题解析
19. 如图，直线AB与x轴相交于点A（1，0），与y轴相交于点B（0，-2）．

(1)、求直线AB对应的函数表达式；

(2)、当x＝2时，求y的值．

查看试题解析

五、实践探究题

20. 6月13日，某港口的潮水高度y(cm)和时间x(h)的部分数据及函数图象如下：
x(h)
…
11
12
13
14
15
16
17
18
…
y(cm)
…
189
137
103
80
101
133
202
260
…

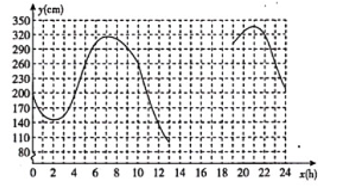(1)、数学活动：①根据表中数据，通过描点、连线(光滑曲线)的方式补全该函数的图象.
②观察函数图象，当x=4时，y的值为多少?当y的值最大时，x的值为多少?

(2)、数学思考：请结合函数图象，写出该函数的两条性质或结论.

(3)、数学应用：根据研究，当潮水高度超过260cm时，货轮能够安全进出该港口.请问当天什么时间段适合货轮进出此港口?

查看试题解析

21. 【建模】春节联欢晚会，九年级生活委员小星先购买了

2

个装饰挂件，共计

3

元，又购买了单价为

2

元的纸杯蛋糕

x

个，设所有装饰挂件和纸杯蛋糕的平均价格为

y

元，则

y

与

x

的关系式为

y = \frac{2 x + 3}{x + 2}

．
【探究】根据函数的概念，小星发现：

y

是

x

的函数，结合自己学习函数的经验，为了更好地研究这个函数，小星打算先脱离实际背景，对该函数的完整图象与性质展开探究，请根据所给信息，将探究过程补充完整

.

列表：

$x$	$\dots$	$- 5$	$- 4$	$- 3$	$- \frac{5}{2}$	$- \frac{3}{2}$	$- 1$	$0$	$1$	$2$	$\dots$
$y$	$\dots$	$\frac{7}{3}$	$\frac{5}{2}$	$m$	$4$	$n$	$1$	$\frac{3}{2}$	$\frac{5}{3}$	$\frac{7}{4}$	$\dots$

(1)、填空：

m =

，

n =

；

(2)、根据函数图象，写出一条该函数的性质；

(3)、【应用】根据上述探究，结合实际经验，小星得到结论：纸杯蛋糕个数越多，所购买物品的平均价格越，

(

填“高”或“低”

)

，但不会超过元

.

查看试题解析

22. 为了市民游玩方便，准备在风阳湖市政森林公国内的环形路上提供免费游览车服务，如图是游览车路线图，已知 $A B$ 间的路程为 $800$ 米， $B C$ 间的路程为 $1000$ 米， $C D$ 间的路程为 $800$ 米， $D A$ 间的路程为 $1000$ 米，现有有 $1$ 号， $2$ 号两游览车分别从出口A和景点 $C$ 同时出发， $1$ 号车逆时针、 $2$ 号车顺时针沿环形路连续循环行驶，供游客随时免费乘车（上，下车的时间忽略不计），两车速度均为 $200$ 米/分．

(1)、探究：设行驶时间为 $t$ 分．
①当 $0 \leq t \leq 9$ 时，分别写出 $1$ 号车， $2$ 号车在下半圈环线离出口A的路程 $y_{1}$ ， $y_{2}$ （米）与 $t$ （分）的函数关系式，并求出当两车相距的路程少于 $400$ 米时 $t$ 的取值范围；
② $t$ 为何值时， $1$ 号车第三次恰好经过景点 $B$ ，并直接写出这一段时间内它与 $2$ 号车相遇过的次数．

(2)、应用：已知游客小双在 $D A$ 上从景点 $D$ 向出口A走去，步行的速度是 $50$ 米/分，当行进到 $D A$ 上一点 $P$ （不与点 $D$ ， A重合）时，刚好与 $2$ 号车迎面相遇，设 $P A$ 的路程为s $(0 < s < 1000)$ 米，写出他原地等候乘 $1$ 号车到出口A所花时间 $T$ 与 $s$ 的函数关系式，并直接写出 $s$ 在什么范围内时，等候乘 $1$ 号车能更快到达．

查看试题解析

六、综合题

23. 某运输公司安排大、小两种货车

15

辆恰好一次性将

152

吨的农用物资运往

A

、

B

两村，两种大、小货车的载货能力分别为

12

吨/辆和

8

吨/辆，其运往

A

、

B

两村的运费如下表：

车型	$A$ 村（元/辆）	$B$ 村（元/辆）
大货车	$800$	$900$
小货车	$400$	$600$

(1)、求大、小货车各用了多少辆？

(2)、现安排前往

A

村的大、小货车共

10

辆，所运物资不少于

100

吨，其余货车将剩余物资运往

B

村，设大、小两种货车到

A

，

B

两村的总运输成本为

w

元，前往

A

村的大货车为

m

辆．写出

w

与

m

之间的函数解析式，当

m

为何值时，调运总费用

w

取得最小值，最少费用是多少？