湘教版数学八年级下学期第3章图形与坐标单元测试B卷

试卷更新日期：2024-04-03 类型：单元试卷

进入出卷网下载

一、选择题

1. 在平面直角坐标系中，点 $(3 ， - 2)$ 关于 $x$ 轴对称的点的坐标是（）．

A、 $(- 3 ， - 2)$ B、 $(3 ， - 2)$ C、 $(- 3 ， 2)$ D、 $(3 ， 2)$

查看试题解析
2. 已知点P（m﹣1，4）与点Q（2，n+2）关于y轴对称，则n^m的值为（　　）

A、﹣2 B、 $\frac{1}{2}$ C、﹣ $\frac{1}{2}$ D、1

查看试题解析
3. 已知点 $P$ 的坐标为 $(2 x ， x + 3)$ ，点 $M$ 的坐标为 $(x + 1 ， 2 x)$ ， $P M$ 平行于 $x$ 轴，则 $M$ 点的坐标（）

A、 $(2 ， 4)$ B、 $(2 ， 2)$ C、 $(6 ， 6)$ D、 $(4 ， 6)$

查看试题解析
4. 如图，边长为2的正方形ABCD的中心与坐标原点 $O$ 重合， $A B / / x$ 轴，将正方形ABCD绕原点 $O$ 顺时针旋2023次，每次旋转 $45 °$ ，则顶点 $B$ 的坐标是（）

A、 $(\sqrt{2} ， - 1)$ B、 $(0 ， - \sqrt{2})$ C、 $(0 ， \sqrt{2})$ D、 $(- 1 ， - 1)$

查看试题解析
5. 将点A（4，1）绕原点O按顺时针方向旋转90°到点B，则点B的坐标是（　　）

A、（1，﹣4） B、（4，﹣1） C、（﹣4，1） D、（﹣1，4）

查看试题解析
6. 如图，在平面直角坐标系中，C（5，5），点B、A分别在x轴正半轴和y轴正半轴上， $∠ A C B ＝ 90 °$ ，则 $O A ＋ O B$ 等于（）

A、8 B、9 C、10 D、11

查看试题解析
7. 若x轴上的点P到y轴的距离为3，则点P为（）

A、（3，0） B、（3，0）或（－3，0） C、（0，3） D、（0，3）或（0，－3）

查看试题解析
8. 平面直角坐标系中，已知A（2，0），B（0，2）若在坐标轴上取C点，使△ABC为等腰三角形，则满足条件的点C的个数是（）

A、4 B、6 C、7 D、8

查看试题解析
9. 如图，将边长为 $\sqrt{3}$ 的正方形ABCD绕点B逆时针旋转30°得到正方形A′BC′D′，AD与C′D′交于点M ，那么图中点M的坐标为（　　）

A、 $(\sqrt{3} ， 1)$ B、 $(1 ， \sqrt{3})$ C、 $(\sqrt{3} ， \frac{\sqrt{3}}{2})$ D、 $(\frac{\sqrt{3}}{2} ， \sqrt{3})$

查看试题解析
10. 在如图所示的方格纸上（小正方形的边长均为1）， $△ A_{1} A_{2} A_{3}$ ， $△ A_{3} A_{4} A_{5}$ ， $△ A_{5} A_{6} A_{7} ， ⋯$ 都是斜边在 $x$ 轴上的等腰直角三角形，且它们的斜边长分别为2，4，6…若 $△ A_{1} A_{2} A_{3}$ 的顶点坐标分别为 $A_{1} (2 ， 0)$ ， $A_{2} (1 ， - 1)$ ， $A_{3} (0 ， 0)$ ，则依图中所示规律， $A_{2022}$ 的坐标为（）

A、 $(1 ， - 1013)$ B、 $(1 ， - 1011)$ C、 $(2 ， 1012)$ D、 $(2 ， 1010)$

查看试题解析

二、填空题

11. 若点 $P (2 ， 3)$ 关于y轴的对称点是点 $P^{'} (a ， 3)$ ，则a= ．

查看试题解析
12. 平面直角坐标系中，点 $(- 1 ， - 2)$ 与点关于y轴对称。

查看试题解析
13. 如图，在平面直角坐标系中，图案由全等的 $4$ 个长方形纸片摆成的 $.$ 若点 $A (- 3，7)$ ，则点 $B$ 的坐标为．

查看试题解析
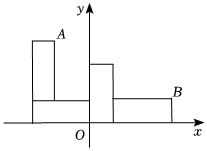14. 如图，在直角坐标系中，长方形OABC的顶点A ， C分别在x轴，y轴上，点A ， C的坐标分别为（﹣7，0），（0，4）．E为边BC上一点，点D的坐标为（﹣5，0），若△ODE是腰长为5的等腰三角形，则点E的坐标是．

查看试题解析
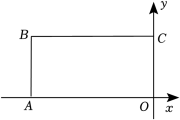15. 如图，直线 $A B$ 与x轴，y轴分别交于点 $A (\sqrt{2} ， 0)$ 和 $B (0 ， - \sqrt{2})$ ，点P是直线 $A B$ 上的一个动点，点P的横坐标为 $t (0 \leq t \leq \sqrt{2})$ ，以线段 $O P$ 为边，点O为直角顶点在y轴右侧作等腰直角 $△ O P Q ， P Q$ 与x轴交于点C．在点P的运动过程中，当t的值 $=$ 时，△OCP为等腰三角形．

查看试题解析

三、作图题

16. 在平面直角坐标系中，已知△ABC的位置如图所示．

(1)、请作出△ABC向右平移5个单位后得到的△A₁B₁C₁（其中点A₁ ， B₁ ， C₁分别是点A ， B ， C的对应点，不写画法）；

(2)、写出点B关于x轴的对称点B₂的坐标．

查看试题解析

四、解答题

17. 已知点 $A (2 a - 4 ， a - 1)$ ，根据条件解决下列问题：

(1)、若点A在y轴上，求点A的坐标；

(2)、若点A在过点 $P (5 ， 2)$ 且与x轴平行的直线上，求线段 $A P$ 的长．

查看试题解析
18. 在平面直角坐标系中，若点 $M (m + 2 ， n - 2)$ 关于 $x$ 轴对称的对称点为点 $M^{'} (1 - n ， 2 m)$ ，求 $m$ ， $n$ 的值．

查看试题解析
19. 如图，在平面直角坐标系中， $A (- 1 ， 5)$ ， $B (- 1 ， 0)$ ， $C (- 4 ， 3)$ ．

(1)、求出 $△ A B C$ 的面积；

(2)、若 $△ A_{1} B_{1} C_{1}$ 与 $△ A B C$ 关于y轴对称，写出点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的坐标．

查看试题解析

五、综合题

20. 平面直角坐标系中，正方形 $O A B C$ 的点 $A$ 在 $y$ 轴上，点 $C$ 在 $x$ 轴上，点 $B (4 ， 4)$ ，另有一动点 $E$ ，连接 $A E$ ．

(1)、如图，当点 $E$ 在 $B C$ 边上时，将 $△ A B E$ 绕点 $A$ 顺时针旋转 $90 °$ ，得到 $△ A O F$ ，连接 $E F$ 交 $y$ 轴于点 $D$ ．
$①$ 若点 $E$ 的坐标为 $(4 ， 3)$ ，求线段 $E F$ 的长；
$②$ 设点 $E (4 ， m)$ ， $S = S_{△ A B E} + S_{△ F C E}$ ，试用含 $m$ 的式子表示 $S$ ；

(2)、当点 $E$ 满足 $A E = O A$ ， $($ 点 $E$ 不与点 $O$ 重合 $)$ ，连接 $O E .$ 现在以 $O$ 为中心，将 $O E$ 顺时针旋转 $60 °$ ，得到 $O P$ ，求当 $A P$ 取得最大值时点 $E$ 的坐标．

查看试题解析
21. 在平面直角坐标系中，O为坐标原点，过点A（8，6）分别作x轴、y轴的平行线，交y轴于点B，交x轴于点C，点P是从点B出发，沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点，运动时间为t（秒）．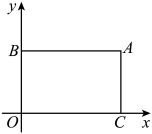

(1)、直接写出点B和点C的坐标．

(2)、当点P运动时，用含t的式子表示线段AP的长，

(3)、点D（2，0），连接PD、AD，在（2）条件下是否存在这样的t值，使 $S_{△ A P D} = \frac{1}{8} S_{四边形 A B O C}$ ，若存在，请求出t值，若不存在，请说明理由．

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，对于任意三点 $A$ ， $B$ ， $C$ 的“矩面积”给出如下定义：“水平底” $a$ ：任意两点横坐标差的最大值，“铅垂高” $h$ ：任意两点纵坐标差的最大值，则“矩面积” $S = a h$ ．
例如：三点的坐标分别为 $A (1 ， 2)$ ， $B (- 2 ， - 1)$ ， $C (2 ， - 3)$ ，则“水平底” $a = 4$ ， “铅垂高” $h = 5$ ， “矩面积” $S = a h = 20$ .

(1)、若 $A (- 1 ， 2)$ ， $B (3 ， 1)$ ， $C (- 3 ， - 2)$ ，则“水平底” $a =$ ， “铅垂高” $h =$ ， “矩面积” $S =$

(2)、若 $A (- 1 ， 2)$ ， $B (3 ， - 1)$ ， $P (0 ， n)$ 的“矩面积”为20，求点 $P$ 的坐标

查看试题解析
23. 如图，在直角坐标系中，直线 $y = \sqrt{3} x - 2 \sqrt{3}$ 交y轴，x轴于点 $A ， B$ ，点D在y轴正半轴上，以 $A B ， A D$ 为边作平行四边形ABCD ，点E从点O出发，以每秒1个单位的速度沿y轴正方向移动，记点E运动时间为t秒．

(1)、直接写出点A的坐标， $A B =$ ；

(2)、若 $O D = 2 O A$ ，连接 $B D ，$ F是 $B D$ 的中点，连接 $E F$ 并延长交直线 $B C$ 于点H ，
①当四边形 $A B H E$ 为平行四边形时，请直接写出t的值；
②当 $△ B F H$ 是以 $B F$ 为腰的等腰三角形时，请直接写出t的值；

(3)、若 $A D = 4 \sqrt{3}$ ，点E在 $O D$ 上，点M位于点E的正上方，且 $∠ E B C + ∠ M C B = 90 °$ ，当四边形 $E B C M$ 的面积最大时，求 $D M$ 的长．

查看试题解析

湘教版数学八年级下学期 第3章 图形与坐标单元 测试B卷

一、选择题

二、填空题

三、作图题

四、解答题

五、综合题

湘教版数学八年级下学期第3章图形与坐标单元测试B卷