湘教版数学八年级下学期 第3章 图形与坐标单元 测试A卷
试卷更新日期:2024-04-03 类型:单元试卷
一、选择题
-
1. 点P(-2,5)关于x轴对称的点的坐标为( )A、(2,-5) B、(5,-2) C、(-2,-5) D、(2,5)2. 在平面直角坐标系中,点(-1,2)在( ).A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 若点M(m+3,m﹣2)在x轴上,则点M的坐标为( )A、(0,﹣5) B、(0,5) C、(﹣5,0) D、(5,0)4. 如图,平面直角坐标系中,线段的两端点坐标分别为 , , 现将该线段沿轴向右平移,使得点与原点重合,得到线段 , 则点的坐标是( )
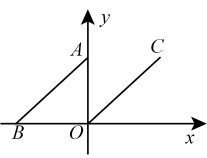 A、 B、 C、 D、5. 若点在第二象限,且到轴的距离是3,到轴的距离是1,则点的坐标是( )A、 B、 C、 D、6. 已知点和关于x轴对称,则的值是( )A、0 B、 C、1 D、7. 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴负半轴于点M,交y轴负半轴于点N,再分别以点M,N为圆心,大于的长为半径画弧,两弧在第三象限交于点P.若点P的坐标为 , 则a与b的数量关系为( )
A、 B、 C、 D、5. 若点在第二象限,且到轴的距离是3,到轴的距离是1,则点的坐标是( )A、 B、 C、 D、6. 已知点和关于x轴对称,则的值是( )A、0 B、 C、1 D、7. 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴负半轴于点M,交y轴负半轴于点N,再分别以点M,N为圆心,大于的长为半径画弧,两弧在第三象限交于点P.若点P的坐标为 , 则a与b的数量关系为( ) A、 B、 C、 D、8. 点P(-1,2)是由点Q(0,-1)经过( )而得到的.A、先向右平移1个长度,再向下平移3个单位长度 B、先向左平移1个长度,再向下平移3个单位长度 C、先向上平移3个长度,再向左平移1个单位长度 D、先向下平移1个长度,再向右平移3个单位长度9. 如图,在平面直角坐标系中,正方形的顶点均在坐标轴上,则点的坐标是( ).
A、 B、 C、 D、8. 点P(-1,2)是由点Q(0,-1)经过( )而得到的.A、先向右平移1个长度,再向下平移3个单位长度 B、先向左平移1个长度,再向下平移3个单位长度 C、先向上平移3个长度,再向左平移1个单位长度 D、先向下平移1个长度,再向右平移3个单位长度9. 如图,在平面直角坐标系中,正方形的顶点均在坐标轴上,则点的坐标是( ). A、 B、 C、 D、10. 如图,在平面直角坐标系中,射线是第一象限的角平分线,线段 , 将绕原点顺时针旋转,每次旋转 , 则第次旋转结束后,点对应点的坐标为( )
A、 B、 C、 D、10. 如图,在平面直角坐标系中,射线是第一象限的角平分线,线段 , 将绕原点顺时针旋转,每次旋转 , 则第次旋转结束后,点对应点的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 同学们玩过五子棋吗?它的比赛规则是只要同色五子先成一条直线就算胜.如图是两人玩的一盘棋,若白①的位置是(1,-5),黑②的位置是(2,-4),现在轮到黑棋走,你认为黑棋放在位置就可获胜.
 12. 如图,四边形是矩形,三点的坐标分别是 , , , 对角线交点为 , 则点的坐标是 .
12. 如图,四边形是矩形,三点的坐标分别是 , , , 对角线交点为 , 则点的坐标是 . 13. 已知点A(0,3),B(6,0),C是x轴正半轴上一点,D是同一平面直角坐标系内一点.若以 A,B,C,D为顶点的四边形是菱形,则点 D 的坐标为.14. 如图,将点绕着原点O逆时针方向旋转得到点B , 则点B的坐标是 .
13. 已知点A(0,3),B(6,0),C是x轴正半轴上一点,D是同一平面直角坐标系内一点.若以 A,B,C,D为顶点的四边形是菱形,则点 D 的坐标为.14. 如图,将点绕着原点O逆时针方向旋转得到点B , 则点B的坐标是 . 15. 在平面直角坐标系xOy中,进行如下操作:把点先向左平移1个单位,再向下平移1个单位到达点;把点先向右平移2个单位,再向上平移2个单位到达点;把点先向左平移3个单位,再向下平移3个单位到达点;把点先向右平移4个单位,再向上平移4个单位到达点;依此规律进行,点的坐标为 .
15. 在平面直角坐标系xOy中,进行如下操作:把点先向左平移1个单位,再向下平移1个单位到达点;把点先向右平移2个单位,再向上平移2个单位到达点;把点先向左平移3个单位,再向下平移3个单位到达点;把点先向右平移4个单位,再向上平移4个单位到达点;依此规律进行,点的坐标为 .
三、作图题
-
16. 如图,在平面直角坐标系中,△ABC 的三个顶点坐标分别为A(1,- 4),B (3,- 3) ,
C(1,- 1).
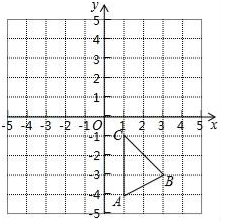 (1)、画出△ABC关于x轴对称的△A1B1C1;(2)、写出△A1B1C1各顶点的坐标;(3)、求△ABC 的面积.
(1)、画出△ABC关于x轴对称的△A1B1C1;(2)、写出△A1B1C1各顶点的坐标;(3)、求△ABC 的面积.四、解答题
-
17. 已知,在平面直角坐标系中的位置如图所示.
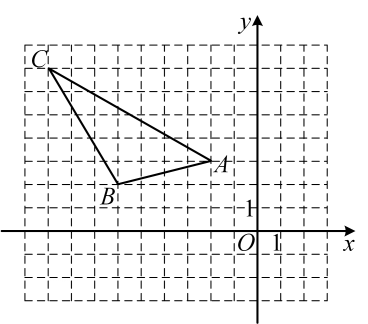 (1)、求的面积.(2)、中任意一点经平移后对应点为 , 将作同样的平移得到 , 请直接写出、、的坐标.18. 如图,在平面直角坐标系中,线段两端点的坐标分别为、 . 平移线段 , 使得点A移到点 , 连接、 . 写出点的坐标,判断四边形的形状并说明理由.
(1)、求的面积.(2)、中任意一点经平移后对应点为 , 将作同样的平移得到 , 请直接写出、、的坐标.18. 如图,在平面直角坐标系中,线段两端点的坐标分别为、 . 平移线段 , 使得点A移到点 , 连接、 . 写出点的坐标,判断四边形的形状并说明理由. 19. 如图 , 点为平面直角坐标系的原点,点在轴上,是边长为的等边三角形.
19. 如图 , 点为平面直角坐标系的原点,点在轴上,是边长为的等边三角形. (1)、求点的坐标;(2)、若将绕点顺时针旋转 , 则点的对应点的坐标是;(3)、将沿着轴向右平移到处,如图 , 连接 , 交于点判断的形状,并说明理由.
(1)、求点的坐标;(2)、若将绕点顺时针旋转 , 则点的对应点的坐标是;(3)、将沿着轴向右平移到处,如图 , 连接 , 交于点判断的形状,并说明理由.五、综合题
-
20. 已知平面直角坐标系上有一点 , 请根据题意回答下列问题:(1)、若点在轴上,求点的坐标;(2)、点的坐标为 , 连接 , 若轴,求的长.21. 如图,在平面直角坐标系中,O为坐标原点,点C在x轴上,点A在y轴上,在四边形中, , 点B的坐标为 , .
 (1)、求点C的坐标;(2)、动点P从点A出发,以每秒1个单位长度的速度沿射线运动,过点P作轴,垂足为H,直线交直线于点Q,设的长度为 , 点P的运动时间为t秒,求d与t之间的函数关系式,并直接写出自变量t的取值范围;(3)、在坐标平面内,是否存在一点M,使得以A,B,C,M为顶点的四边形为平行四边形?如果存在,请直接写出点M的坐标;如果不存在,请说明理由.22. 与在平面直角坐标系中的位置如图所示.
(1)、求点C的坐标;(2)、动点P从点A出发,以每秒1个单位长度的速度沿射线运动,过点P作轴,垂足为H,直线交直线于点Q,设的长度为 , 点P的运动时间为t秒,求d与t之间的函数关系式,并直接写出自变量t的取值范围;(3)、在坐标平面内,是否存在一点M,使得以A,B,C,M为顶点的四边形为平行四边形?如果存在,请直接写出点M的坐标;如果不存在,请说明理由.22. 与在平面直角坐标系中的位置如图所示.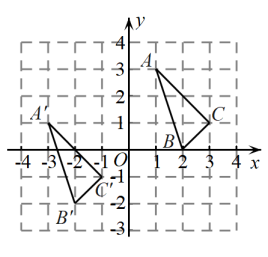 (1)、分别写出下列各点的坐标:A , A';(2)、若点是内部一点,则内部的对应点的坐标为;(3)、是由经过怎样的平移得到的?
(1)、分别写出下列各点的坐标:A , A';(2)、若点是内部一点,则内部的对应点的坐标为;(3)、是由经过怎样的平移得到的?
-