湘教版数学八年级下学期 第2章 四边形 单元测试B卷
试卷更新日期:2024-04-03 类型:单元试卷
一、选择题
-
1. 下列关于数字变换的图案中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 七边形的对角线一共有( )条A、14 B、21 C、28 D、423. 矩形、菱形、正方形都具有的性质是( )A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线互相平分且相等4. 如图,矩形ABCD的对角线AC,BD相交于点O,AB=6,∠ACB=30°,则OD的长为( )
2. 七边形的对角线一共有( )条A、14 B、21 C、28 D、423. 矩形、菱形、正方形都具有的性质是( )A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线互相平分且相等4. 如图,矩形ABCD的对角线AC,BD相交于点O,AB=6,∠ACB=30°,则OD的长为( ) A、6 B、8 C、10 D、125. 如图,在菱形中,是的中点, , 交于点 , 如果 , 那么菱形的周长为
A、6 B、8 C、10 D、125. 如图,在菱形中,是的中点, , 交于点 , 如果 , 那么菱形的周长为 A、 B、 C、 D、6. 如图,在▱ABCD中,O是对角线AC上一点,连结 BO,DO.若△COD,△AOD,△AOB,△BOC 的面积分别为 S1 , S2 , S3 , S4 , 则下列关于 S1 , S2 , S3 , S4的等量关系中,不一定正确的是( )
A、 B、 C、 D、6. 如图,在▱ABCD中,O是对角线AC上一点,连结 BO,DO.若△COD,△AOD,△AOB,△BOC 的面积分别为 S1 , S2 , S3 , S4 , 则下列关于 S1 , S2 , S3 , S4的等量关系中,不一定正确的是( ) A、 B、 C、 D、7. 如图,F是正方形ABCD 对角线BD上一点,连结AF,CF,延长CF交AD 于点E.若∠AFC=140°,则∠DEC的度数为 ( )
A、 B、 C、 D、7. 如图,F是正方形ABCD 对角线BD上一点,连结AF,CF,延长CF交AD 于点E.若∠AFC=140°,则∠DEC的度数为 ( ) A、80° B、75° C、70° D、65°8. 如图,在中, , 以的各边为边作三个正方形,点G落在上,若 , 空白部分面积为10.5,则的长为( )
A、80° B、75° C、70° D、65°8. 如图,在中, , 以的各边为边作三个正方形,点G落在上,若 , 空白部分面积为10.5,则的长为( )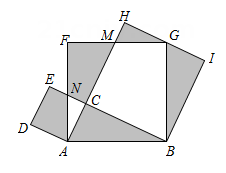 A、 B、 C、 D、9. 如图,正方形 的面积为 , 是等边三角形,点 在正方形 内,在对角线 上有一点 ,使 的和最小,则这个最小值为( ).
A、 B、 C、 D、9. 如图,正方形 的面积为 , 是等边三角形,点 在正方形 内,在对角线 上有一点 ,使 的和最小,则这个最小值为( ).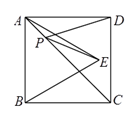 A、 B、 C、 D、10. 如图,矩形的对角线相交于点O , F是上的一点,连接 , 将沿翻折,点C恰好与点O重合,延长交于点E , 连接 . 则下列结论:①是等边三角形;②;③四边形是菱形;④ , 其中正确结论的个数是( )
A、 B、 C、 D、10. 如图,矩形的对角线相交于点O , F是上的一点,连接 , 将沿翻折,点C恰好与点O重合,延长交于点E , 连接 . 则下列结论:①是等边三角形;②;③四边形是菱形;④ , 其中正确结论的个数是( ) A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
11. 已知正n边形的一个外角是 , 则 .12. 如图,在边长为2的正方形ABCD中,E,F分别是BC,CD上的动点,M,N分别是EF,AF的中点,则MN的最大值为
 13. 如图,将边长为 6 cm的正方形纸片 ABCD折叠,使点 D 落在AB边的中点 E 处,点 C 落在点Q处,折痕为 FH,则线段 AF的长为cm.
13. 如图,将边长为 6 cm的正方形纸片 ABCD折叠,使点 D 落在AB边的中点 E 处,点 C 落在点Q处,折痕为 FH,则线段 AF的长为cm. 14. 如图,边长为5的大正方形ABCD是由四个全等的直角三角形和一个小正方形EFGH组成,连结AF并延长交BC于点M . 若AH=HE , 则CM的长为 .
14. 如图,边长为5的大正方形ABCD是由四个全等的直角三角形和一个小正方形EFGH组成,连结AF并延长交BC于点M . 若AH=HE , 则CM的长为 . 15. 如图,在中, , 以为边向上作正方形 , 以为边作正方形 , 点D落在上,连接 , . 若 , , 则的面积为 .
15. 如图,在中, , 以为边向上作正方形 , 以为边作正方形 , 点D落在上,连接 , . 若 , , 则的面积为 .
三、作图题
-
16. 在平面直角坐标系中,已知四边形ABCD四个顶点坐标分别为A(0,4),B(1,0),C(3,0),D(4,4).
 (1)、在如图所示的平面直角坐标系中画出四边形ABCD;(2)、画出四边形ABCD关于x轴对称的四边形A1B1C1D1 , 并直接写出点D的对称点D1的坐标;(3)、若四边形ABCD上的点P坐标为(x,y),则其关于x轴对称点坐标为 .
(1)、在如图所示的平面直角坐标系中画出四边形ABCD;(2)、画出四边形ABCD关于x轴对称的四边形A1B1C1D1 , 并直接写出点D的对称点D1的坐标;(3)、若四边形ABCD上的点P坐标为(x,y),则其关于x轴对称点坐标为 .四、解答题
-
17. 如图,△ABC是等边三角形,点D是边BC上的一点,以AD为边作等边△ADE,过点C作CF∥DE交AB于点F.
 (1)、若点D是BC边的中点(如图①) ,求证:EF=CD.(2)、在(1)的条件下直接写出△AEF和△ABC的面积比.(3)、若点D是BC边上的任意一点(除B,C外,如图②) ,那么(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.18. 已知P是等边三角形ABC的边BC上的一点,若∠APC=104°,则在以线段AP,BP,CP为边的三角形中,求最小内角的度数.19. 如图,在▱ABCD中,BE,DG分别平分∠ABC,∠ADC,点E,G在AC上.
(1)、若点D是BC边的中点(如图①) ,求证:EF=CD.(2)、在(1)的条件下直接写出△AEF和△ABC的面积比.(3)、若点D是BC边上的任意一点(除B,C外,如图②) ,那么(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.18. 已知P是等边三角形ABC的边BC上的一点,若∠APC=104°,则在以线段AP,BP,CP为边的三角形中,求最小内角的度数.19. 如图,在▱ABCD中,BE,DG分别平分∠ABC,∠ADC,点E,G在AC上. (1)、求证:BE∥DG,BE=DG.(2)、过点E作EF⊥AB,垂足为F.若▱ABCD的周长为56,EF=6,求△ABC的面积.
(1)、求证:BE∥DG,BE=DG.(2)、过点E作EF⊥AB,垂足为F.若▱ABCD的周长为56,EF=6,求△ABC的面积.五、实践探究题
-
20. 乐乐和数学小组的同学们研究多边形对角线的相关问题,邀请你也加入其中!请仔细观察下面的图形和表格,并回答下列问题:

多边形的顶点数
4
5
6
7
8
……
n
从一个顶点出发的对角线条数
1
2
3
4
5
……
多边形对角线的总条数
2
5
9
14
20
……
(1)、观察探究:请观察上面的图形和表格,并用含n的代数式将上面的表格填写完整;(2)、实际应用:数学社团共分为6个小组,每组有3名同学.同学们约定,大年初一时不同组的两位同学之间要打一个电话拜年,请问,按照此约定,数学社团的同学们一共将拨打多少个电话?21. 如图,在△ABC中,已知∠BAC =45°,AD⊥BC于点 D,BD=2,DC=3,求AD 的长.小萍同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题.
请按照小萍同学的思路,探究并解答下列问题:
 (1)、分别以 AB,AC 为对称轴,作出△ABD,△ACD的轴对称图形,点 D 的对称点分别为E,F,延长 EB,FC相交于点G.求证:四边形AEGF 是正方形.(2)、设 AD=x,利用勾股定理,建立关于 x的方程,求出 AD的长.22. [创新意识]
(1)、分别以 AB,AC 为对称轴,作出△ABD,△ACD的轴对称图形,点 D 的对称点分别为E,F,延长 EB,FC相交于点G.求证:四边形AEGF 是正方形.(2)、设 AD=x,利用勾股定理,建立关于 x的方程,求出 AD的长.22. [创新意识] (1)、【探究问题】如图1,已知 l1∥l2 , 点 A,D在直线l1上,点 B,C在直线l2上,连结 AB,AC,BD,CD,AC 与BD 相交于点O.问:图中面积相等的三角形有几对? 请分别将它们写出来.(2)、【拓展运用】如图2,请把四边形ABCD分成面积相等的两部分.
(1)、【探究问题】如图1,已知 l1∥l2 , 点 A,D在直线l1上,点 B,C在直线l2上,连结 AB,AC,BD,CD,AC 与BD 相交于点O.问:图中面积相等的三角形有几对? 请分别将它们写出来.(2)、【拓展运用】如图2,请把四边形ABCD分成面积相等的两部分.六、综合题
-
23. 如图,在长方形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE , 将∠B沿直线AE折叠,使点B落在点B'处.
 (1)、如图1,当点E与点C重合时,CB'与AD交于点F , 求证:FA=FC;(2)、如图2,当点E不与点C重合,且点B'在对角线AC上时,求CE的长.24. 已知:AC是菱形ABCD的对角线,且AC=BC.
(1)、如图1,当点E与点C重合时,CB'与AD交于点F , 求证:FA=FC;(2)、如图2,当点E不与点C重合,且点B'在对角线AC上时,求CE的长.24. 已知:AC是菱形ABCD的对角线,且AC=BC. (1)、如图①,点P是△ABC的一个动点,将△ABP绕着点B旋转得到△CBE.
(1)、如图①,点P是△ABC的一个动点,将△ABP绕着点B旋转得到△CBE.①求证:△PBE是等边三角形;
②若BC=5,CE=4,PC=3,求∠PCE的度数;
(2)、连结BD交AC于点O,点E在OD上且DE=3,AD=4,点G是△ADE内的一个动点如图②,连结AG,EG,DG,求AG+EG+DG的最小值.25. 综合与实践问题:给你两个大小不等的正方形,你能通过切割把他们拼接成一个大正方形吗?
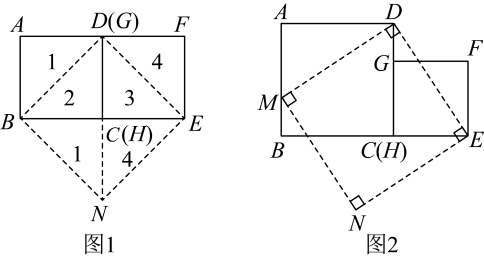
下面是某研究小组的研究过程:
(1)、首先研究两个一样大小的正方形把两个边长相等的正方形和正方形 , 按图1所示的方式摆放,沿虚线、剪开后,可按图1所示的移动方式拼接成四边形形 , 则四边形形是正方形,请说明理由;
(2)、研究大小不等的两个正方形把边长不等的两个正方形和正方形 , 按图2所示的方式摆放,连接 , 过点D作 , 交于点M , 过点M作 , 过点E作 , 与相交于点N .
①证明四边形是正方形;
②在图2中,将正方形和正方形沿虚线剪开后,能够拼接为正方形 , 请简略说明你的拼接方法(类比图1,用数字表示对应的图形).
-