湘教版数学八年级下学期 第1章 直角三角形 单元测试B卷
试卷更新日期:2024-04-03 类型:单元试卷
一、选择题
-
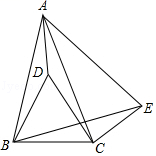
1. 下列各组长度的线段,不能组成直角三角形的是( )A、5,12,13 B、 C、2,3,4 D、6,8,102. 如图,O是△ABC的三条角平分线的交点,连接OA,OB,OC,若△OAB,△OBC,△OAC的面积分别为S1 , S2 , S3 , 则下列关系正确的是( )
 A、S1>S2+S3 B、S1=S2+S3 C、S1<S2+S3 D、无法确定3. 如图,在中, , 为上一点,且 , , , 则的面积为( )
A、S1>S2+S3 B、S1=S2+S3 C、S1<S2+S3 D、无法确定3. 如图,在中, , 为上一点,且 , , , 则的面积为( ) A、6 B、7 C、10 D、94. 如图,嘉嘉在A时测得一棵高的树的影长为 , 若A时和B时两次日照的光线互相垂直,则B时的影长为( )
A、6 B、7 C、10 D、94. 如图,嘉嘉在A时测得一棵高的树的影长为 , 若A时和B时两次日照的光线互相垂直,则B时的影长为( ) A、 B、 C、 D、5. 在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于点D , BC=7,BD=4,则点D到AB的距离是( )
A、 B、 C、 D、5. 在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于点D , BC=7,BD=4,则点D到AB的距离是( )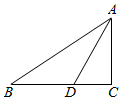 A、3 B、4 C、5 D、76. 如图,在中,于D , , 则( )
A、3 B、4 C、5 D、76. 如图,在中,于D , , 则( ) A、2 B、3 C、2.5 D、1.57. 如图,在中, , 以 , , 为边作等边 , 等边 , 等边 . 设的面积为 , 的面积为 , 的面积为 , 四边形的面积为 , 则下列结论正确的是( )
A、2 B、3 C、2.5 D、1.57. 如图,在中, , 以 , , 为边作等边 , 等边 , 等边 . 设的面积为 , 的面积为 , 的面积为 , 四边形的面积为 , 则下列结论正确的是( )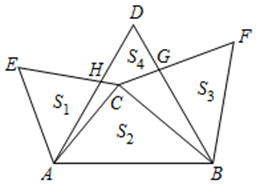 A、 B、 C、 D、8. 由四个全等的直角三角形和一个小正方形EFGH组成的大正方形ABCD如图所示.连结CF,并延长交AB于点N.若AB=3 , EF=3,则FN的长为( )
A、 B、 C、 D、8. 由四个全等的直角三角形和一个小正方形EFGH组成的大正方形ABCD如图所示.连结CF,并延长交AB于点N.若AB=3 , EF=3,则FN的长为( ) A、2 B、 C、 D、39. 如图,在△ABC中,∠ACB=90°,AC=2,AB=4,将△ABC绕点C按逆时针方向旋转一定的角度得到△DEC,使得A点恰好落在DE上,则线段BD的长为( )
A、2 B、 C、 D、39. 如图,在△ABC中,∠ACB=90°,AC=2,AB=4,将△ABC绕点C按逆时针方向旋转一定的角度得到△DEC,使得A点恰好落在DE上,则线段BD的长为( )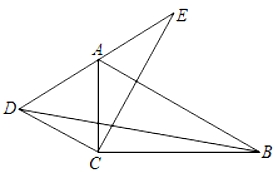 A、2 B、5 C、2 D、310. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EFBC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°∠A,②∠EBO∠AEF,③∠DOC+∠OCB=90°,④设OD=m,AE+AF=n,则S△AEF . 其中正确的结论有( )
A、2 B、5 C、2 D、310. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EFBC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°∠A,②∠EBO∠AEF,③∠DOC+∠OCB=90°,④设OD=m,AE+AF=n,则S△AEF . 其中正确的结论有( )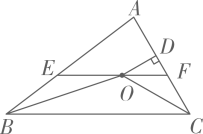 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图, , 点是上一点,点与点关于对称,于点 , 若 , 则的长为 .
 12. 如图,在△ABC中,AB=AC , AD平分∠BAC , DE⊥AB于点E , BF⊥AC于点F , DE=1.3cm , 则BF=cm .
12. 如图,在△ABC中,AB=AC , AD平分∠BAC , DE⊥AB于点E , BF⊥AC于点F , DE=1.3cm , 则BF=cm . 13. 在平面直角坐标系中,将一副三角板按如图所示的方式摆放,BO、DO分别与.动点在边上运动,动点在边上运动,的中点的坐标为 , 则的最小值是.
13. 在平面直角坐标系中,将一副三角板按如图所示的方式摆放,BO、DO分别与.动点在边上运动,动点在边上运动,的中点的坐标为 , 则的最小值是. 14. 如图,在中, , , , 绕顶点逆时针旋转到处,此时线段与的交点为的中点,则线段的长度为 .
14. 如图,在中, , , , 绕顶点逆时针旋转到处,此时线段与的交点为的中点,则线段的长度为 . 15. 如图,是等腰的角平分线, , , 过点作的垂线,过点作的平行线,两线交于点与交于 , 与交于 , 连接 , 点是线段上的动点,点是线段上的动点,连接 , , 下列四个结论:;;;;其中正确的是 填写序号
15. 如图,是等腰的角平分线, , , 过点作的垂线,过点作的平行线,两线交于点与交于 , 与交于 , 连接 , 点是线段上的动点,点是线段上的动点,连接 , , 下列四个结论:;;;;其中正确的是 填写序号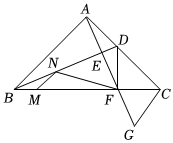
三、作图题
-
16. 如图,在网格中,每个小正方形边长为1个单位长度,我们把每个小正方形的顶点称为格点,均为格点,请按要求仅用一把无刻度的直尺作图,画图过程用虚线表示,画图结果用实线表示.
 (1)、在图1中,作(D在下方),且;(2)、在图1中;作的中点 , 在线段上作点 , 使得;(3)、在图2中;在线段上作点 , 使得;(4)、在图2中,已知 , 在上作点 , 使得 .
(1)、在图1中,作(D在下方),且;(2)、在图1中;作的中点 , 在线段上作点 , 使得;(3)、在图2中;在线段上作点 , 使得;(4)、在图2中,已知 , 在上作点 , 使得 .四、解答题
-
17. 如图,在△ABC中,AB=AC=5,BC=6,点D在AC边上,BD=AB .
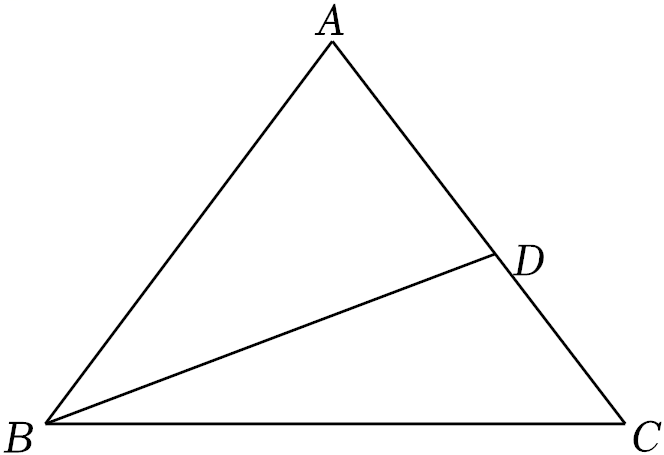 (1)、求△ABC的面积;(2)、求AD的长.18. 如图,点F在线段AB上,点E , G在线段CD上,AB∥CD , ∠1=∠2.
(1)、求△ABC的面积;(2)、求AD的长.18. 如图,点F在线段AB上,点E , G在线段CD上,AB∥CD , ∠1=∠2. (1)、求证:FG∥AE;(2)、若FG⊥BC于点H , BC平分∠ABD , ∠D=120°,求∠1的度数.19. 如图,在△ABC中,∠BAC=90°,AB=AC , DC⊥AC , 垂足为C , AD交线段BC于F , E是AC边上一点,连接BE , 交AD于点G且BE=AD .
(1)、求证:FG∥AE;(2)、若FG⊥BC于点H , BC平分∠ABD , ∠D=120°,求∠1的度数.19. 如图,在△ABC中,∠BAC=90°,AB=AC , DC⊥AC , 垂足为C , AD交线段BC于F , E是AC边上一点,连接BE , 交AD于点G且BE=AD .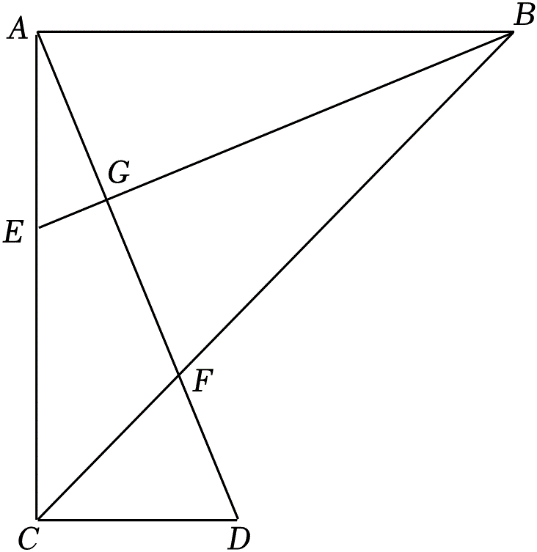 (1)、猜猜BE与AD有怎样的位置关系?说说你的理由;(2)、若BE是∠ABC的角平分线,试说明△CFD是等腰三角形.
(1)、猜猜BE与AD有怎样的位置关系?说说你的理由;(2)、若BE是∠ABC的角平分线,试说明△CFD是等腰三角形.五、实践探究题
-
20. 八年级学生芳芳放学后去幼儿园接弟弟回家,姐弟俩双手相牵在幼儿园门口开心地旋转起来.芳芳突然想起某天数学活动课上老师提出的一个问题:如图,在△AOB和△EOF中,OA=OB , OE=OF , 且∠1=∠2,连接AE , BF交于点M . 试猜想AE与BF的数量关系,并加以证明.
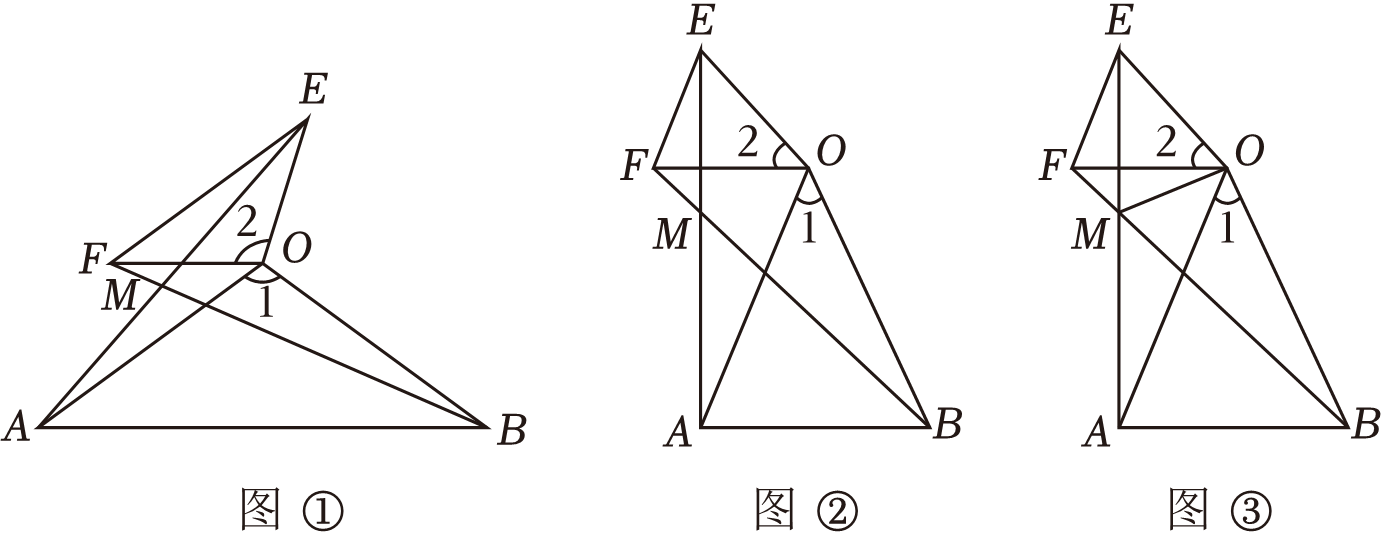 (1)、独立思考:如图①,请解决老师提出的问题。(2)、实践探究:如图②.当∠1=45°时,∠AMB=度;当∠OAB=65°时,∠AMB=度;(3)、解决问题:如图③,连接OM , MO平分∠BME吗?并加以说明.21. 综合与实践
(1)、独立思考:如图①,请解决老师提出的问题。(2)、实践探究:如图②.当∠1=45°时,∠AMB=度;当∠OAB=65°时,∠AMB=度;(3)、解决问题:如图③,连接OM , MO平分∠BME吗?并加以说明.21. 综合与实践【动手操作】
数学活动课上,老师让同学们探究用尺规作图作一条直线的平行线.已知:如图1,直线l及直线l外一点A . 求作:直线 , 使得 . 小明同学设计的做法如下:
①在直线l上取两点B、C , 连接 , 以点B为圆心,小于的长度为半径作弧,交线段于点D , 交线段于点E;
②分别以点D和E为圆心,以大于的长为半径作弧,两弧在内交于点F , 作射线BF;
③以点A为圆心,的长为半径作弧,交射线于点P , 作直线 .
则直线平行于直线l .
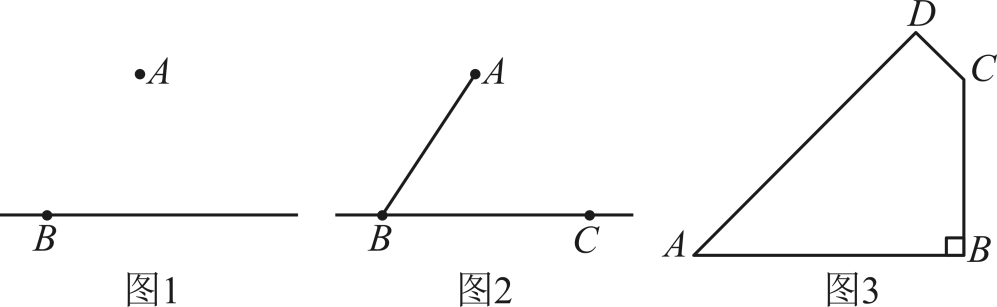 (1)、根据小明同学设计的尺规作图过程,在图2中补全图形;(要求:尺规作图并保留作图痕迹)(2)、【验证证明】
(1)、根据小明同学设计的尺规作图过程,在图2中补全图形;(要求:尺规作图并保留作图痕迹)(2)、【验证证明】请证明直线;
(3)、【拓展延伸】已知:如果两条直线平行,则其中一条直线上任意两点到另外一条直线的距离相等.在图2中连接 , , 请直接写出与的面积关系;
(4)、【应用实践】某市政府为发展新能源产业,决定在如图3所示的四边形空地上划出20km2区域用于建设新能源产业发展基地.已知在四边形中, , km,km.为便于运营管理,某公司向政府提出在线段上取一点E使得四边形的面积为20km2 , 则km.
22. 问题情境:在学习了《勾股定理》和《实数》后,某班同学们以“已知三角形三边的长度,求三角形面积”为主题开展了数学活动,同学们想到借助曾经阅读的数学资料进行探究:材料1.古希腊的几何学家海伦(Heron,约公元50年),在他的著作《度量》一书中,给出了求其面积的海伦公式(其中a,b,c为三角形的三边长, , S为三角形的面积).
材料2.我国南宋时期数学家秦九韶曾提出利用三角形的三边长求面积的秦九韶公式:S= , 其中三角形边长分别为a,b,c,三角形的面积为S.
(1)、利用材料1解决下面的问题:当 时,求这个三角形的面积?(2)、利用材料2解决下面的问题:已知△ABC三条边的长度分别是 , , , 记△ABC的周长为C△ABC .①当x=2时,请直接写出△ABC中最长边的长度;
②若x为整数,当C△ABC取得最大值时,请用秦九韶公式求出△ABC的面积.
六、综合题
-
23. 如图,以直线上一点为端点作射线 , 使 , 将一个直角三角形的直角顶点放在点O处.(注:)
 (1)、如图①,若直角三角板的一边放在射线上,则;(2)、如图②,将直角三角板绕点O逆时针方向转动到某个位置,若恰好平分 , 求的度数;(3)、如图③,将直角三角板绕点O转动,如果始终在的内部,试猜想和有怎样的数量关系?并说明理由.
(1)、如图①,若直角三角板的一边放在射线上,则;(2)、如图②,将直角三角板绕点O逆时针方向转动到某个位置,若恰好平分 , 求的度数;(3)、如图③,将直角三角板绕点O转动,如果始终在的内部,试猜想和有怎样的数量关系?并说明理由.
-