湘教版数学八年级下学期 第1章 直角三角形 单元测试A卷
试卷更新日期:2024-04-03 类型:单元试卷
一、选择题
-
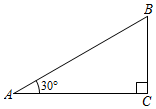
1. 在下列长度的各组线段中,能组成直角三角形的是( )。A、5,6,7 B、5,12,13 C、1,4,9 D、5,11,122. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,则AB等于( )
 A、2 B、3 C、4 D、63. 如图,在中, , , D为上一点, , 则的长为( )
A、2 B、3 C、4 D、63. 如图,在中, , , D为上一点, , 则的长为( ) A、8 B、7 C、6 D、54. 以直角三角形的三边为边向外作正方形,其中两个正方形的面积如图所示,则正方形A的面积为( )
A、8 B、7 C、6 D、54. 以直角三角形的三边为边向外作正方形,其中两个正方形的面积如图所示,则正方形A的面积为( ) A、6 B、36 C、64 D、85. 如图所示,在△ABC中, , , DE为AB的中垂线, , 则CD的长是( )
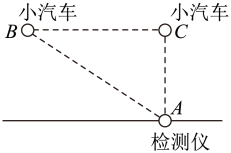
A、6 B、36 C、64 D、85. 如图所示,在△ABC中, , , DE为AB的中垂线, , 则CD的长是( ) A、3 B、4 C、6 D、86. 如图,l1∥l2∥l3 , 且相邻两条直线间的距离都是2,A,B,C分别为l1 , l2 , l3上的动点,连结AB ,AC,BC,AC与l2交于点D,∠ABC= 90°,则BD的最小值为( )
A、3 B、4 C、6 D、86. 如图,l1∥l2∥l3 , 且相邻两条直线间的距离都是2,A,B,C分别为l1 , l2 , l3上的动点,连结AB ,AC,BC,AC与l2交于点D,∠ABC= 90°,则BD的最小值为( ) A、2 B、3 C、4 D、57. 在长为 , 宽为的长方形硬纸板中剪掉一个直角三角形,以下四种剪法中,裁剪线长度所示的数据(单位:)不正确的是( )A、
A、2 B、3 C、4 D、57. 在长为 , 宽为的长方形硬纸板中剪掉一个直角三角形,以下四种剪法中,裁剪线长度所示的数据(单位:)不正确的是( )A、 B、
B、 C、
C、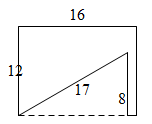 D、
D、 8. 如图,有一块直角三角形纸片,两直角边AB=6,BC=8,将△ABC折叠,使AB落在斜边AC上,折痕为AD , 则BD的长为( )
8. 如图,有一块直角三角形纸片,两直角边AB=6,BC=8,将△ABC折叠,使AB落在斜边AC上,折痕为AD , 则BD的长为( )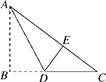 A、3 B、4 C、5 D、69. 如图,在△ABC中,∠C=90°,∠A=30°,AB的垂直平分线分别交AB,AC于点D,E,则下列结论正确的是( )
A、3 B、4 C、5 D、69. 如图,在△ABC中,∠C=90°,∠A=30°,AB的垂直平分线分别交AB,AC于点D,E,则下列结论正确的是( ) A、AE=3CE B、AE=2CE C、AE=BD D、BC=2CE10. 小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm , 接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )
A、AE=3CE B、AE=2CE C、AE=BD D、BC=2CE10. 小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm , 接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )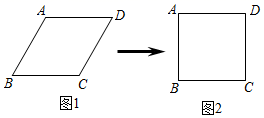 A、20cm B、30cm C、40cm D、20 cm
A、20cm B、30cm C、40cm D、20 cm二、填空题
-
11. 已知直角三角形的一个锐角为36°,则另一个锐角的大小为.12. 在Rt△ABC中,已知∠C=90°,∠B=46°,则∠A的度数为 .13. 如图,在△ABC中,∠C=90°,∠A=15°,∠DBC=60°,BC= , 则AD的长为 .
 14. 如图,将三角形纸片ABC沿AD折叠,使点C落在BD边上的点E处.若BC=10,BE=2,则AB2﹣AC2的值为 .
14. 如图,将三角形纸片ABC沿AD折叠,使点C落在BD边上的点E处.若BC=10,BE=2,则AB2﹣AC2的值为 .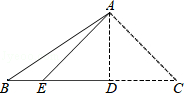 15. 如图,在中, , 点分别在边上,连接 , 若 , 且是等边三角形,则 .
15. 如图,在中, , 点分别在边上,连接 , 若 , 且是等边三角形,则 .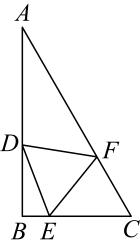
三、解答题
-
16. 如图,在四边形ABCD中,∠ABC=120°,AB⊥AD,BC⊥CD,AB=4,CD=5.求四边形ABCD的面积.
 17. 如图,长方形 ABCD与长方形AEFG 是全等图形,延长 CD 交 FG 于点 M,连结 AM.设AE 与 CD 相交于点 N,求证:△AMN 是等腰三角形.
17. 如图,长方形 ABCD与长方形AEFG 是全等图形,延长 CD 交 FG 于点 M,连结 AM.设AE 与 CD 相交于点 N,求证:△AMN 是等腰三角形. 18. 如图, 在 Rt 中, 于点 . 求 得长.
18. 如图, 在 Rt 中, 于点 . 求 得长.
四、实践探究题
-
19. 阅读下面的情景对话,然后解答问题:
老师:我们新定义一种三角形,两边平方和等于第三边平方的倍的三角形叫做奇异三角形.
小华:等边三角形一定是奇异三角形并做了如下证明:
设等边三角形的边长为 ,
,
等边三角形一定是奇异三角形.
小明:那直角三角形是否存在奇异三角形呢?
(1)、在中,两直角边长分别是、 , 这个三角形是否是奇异三角形?请说明理由.(2)、在中, , , , , 且 , 若是奇异三角形,求::的值.20. 勾股定理是人类重大科学发现之一.我国古代数学书《周髀算经》记载,约公元前11世纪,我国古代劳动人民就知道“若勾三,股四,则弦五”,比西方早500多年.请你运用学到的知识、方法和思想探究以下问题.(1)、(探究一)我国汉代数学家赵爽创制了“赵爽弦图”,通过图形切割、拼接,巧妙地利用面积关系证明了勾股定理.古往今来,人们对勾股定理的证明一直保持着极大的热情.意大利著名画家达·芬奇用两张一样的纸片,拼出不一样的空洞,利用空洞面积相等也成功地证明了勾股定理(如图).请你写出这一证明过程(图中所有的四边形都是正方形,三角形都是直角三角形).
 (2)、(探究二)在学习勾股定理的过程中,我们获得了以下数学活动经验:分别以直角三角形的三边为边向外侧作正方形(如图2),它们的面积 , , 之间满足的等量关系是: .
(2)、(探究二)在学习勾股定理的过程中,我们获得了以下数学活动经验:分别以直角三角形的三边为边向外侧作正方形(如图2),它们的面积 , , 之间满足的等量关系是: . (3)、迁移应用:如图3,图中所有的四边形都是正方形,三角形都是直角三角形.若正方形 , , , 的边长分别是 , , , ,则正方形 的面积是 .
(3)、迁移应用:如图3,图中所有的四边形都是正方形,三角形都是直角三角形.若正方形 , , , 的边长分别是 , , , ,则正方形 的面积是 . (4)、(探究三)如图4,分别以直角三角形的三边为直径向外侧作半圆,则它们的面积 , , 之间满足的等量关系是 .
(4)、(探究三)如图4,分别以直角三角形的三边为直径向外侧作半圆,则它们的面积 , , 之间满足的等量关系是 . (5)、迁移应用:如图5,直角三角形的两条直角边长分别为 , ,斜边长为 ,分别以三边为直径作半圆.若 , ,则图中阴影部分的面积等于 .
(5)、迁移应用:如图5,直角三角形的两条直角边长分别为 , ,斜边长为 ,分别以三边为直径作半圆.若 , ,则图中阴影部分的面积等于 . (6)、(探究四)《九章算术》卷九“勾股”中记载:今有立木,系索其末,委地三尺.引索却行,去本八尺而索尺.问索长几何.译文:今有一竖立着的木柱,在木桩的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有 尺.牵着绳索(绳索与地面接触)退行,在距木柱根部 尺处时绳索用尽.问绳索长多少?
(6)、(探究四)《九章算术》卷九“勾股”中记载:今有立木,系索其末,委地三尺.引索却行,去本八尺而索尺.问索长几何.译文:今有一竖立着的木柱,在木桩的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有 尺.牵着绳索(绳索与地面接触)退行,在距木柱根部 尺处时绳索用尽.问绳索长多少?
五、综合题
-
21. 如图,在4×3正方形网格中,每个小正方形的边长都是1.
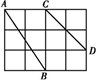 (1)、分别求出线段AB,CD的长度;(2)、在图中画线段EF,使得EF的长为 ,以AB,CD,EF三条线段能否构成直角三角形,并说明理由.
(1)、分别求出线段AB,CD的长度;(2)、在图中画线段EF,使得EF的长为 ,以AB,CD,EF三条线段能否构成直角三角形,并说明理由.