浙江省2024年中考第一次模拟考试数学卷

试卷更新日期：2024-04-02 类型：中考模拟

进入出卷网下载

一、选择题（本大题共10个小题，每小题3分，共30分．在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑）

1. 设x是用字母表示的有理数，则下列各式中一定大于零的是（）

A、 $x + 2$ B、 $2 x$ C、 $| x |$ D、 $x^{2} + 2$

查看试题解析
2. 下列计算正确的是（）

A、 $2 m + 3 n = 5 m n$ B、 $- a^{2} b + b a^{2} = 0$ C、 $x^{2} + 2 x^{2} = 3 x^{4}$ D、 $3 (a + b) = 3 a + b$

查看试题解析
3. 2023年9月23日第19届杭州亚运会开幕，有最高2640000人同时收看直播，数字2640000用科学记数法可以表示为（）

A、 $2.64 \times 1 0^{4}$ B、 $2.64 \times 1 0^{5}$ C、 $2.64 \times 1 0^{6}$ D、 $2.64 \times 1 0^{7}$

查看试题解析
4. 由6个同样的立方体摆出从正面看是的几何体，下面摆法正确的是（）

A、 B、 C、 D、

查看试题解析
5. 分式 $\frac{x^{2} + 2}{x^{2} + 1}$ 的值，可以等于（）

A、 $- 1$ B、0 C、1 D、2

查看试题解析
6. 如图， $B C$ 是 $⊙ O$ 的切线，点 $B$ 是切点，连接 $C O$ 交 $⊙ O$ 于点 $D$ ，延长 $C O$ 交 $⊙ O$ 于点 $A$ ，连接 $A B$ ，若 $∠ C = 30 °$ ， $O D = 2$ ，则 $A B$ 的长为（）

A、 $2 \sqrt{2}$ B、 $3 \sqrt{2}$ C、 $2 \sqrt{3}$ D、 $3 \sqrt{3}$

查看试题解析
7. 小明所在的班级有20人去体育场观看演出，20张票分别为 $A$ 区第10排1号到20号.采用随机抽取的办法分票，小明第一个抽取得到10号座位，接着小亮从其余的票中任意抽取一张，取得的一张恰与小明邻座的概率是（）

A、 $\frac{2}{19}$ B、 $\frac{1}{19}$ C、 $\frac{1}{20}$ D、 $\frac{1}{10}$

查看试题解析
8. 已知 $y_{1}$ 和 $y_{2}$ 均是以x为自变量的函数，当 $x = m$ 时，函数值分别是 $M_{1}$ 和 $M_{2}$ ，若存在实数m ，使得 $M_{1} - M_{2} = 1$ ，则称函数 $y_{1}$ 和 $y_{2}$ 符合“特定规律”，以下函数 $y_{1}$ 和 $y_{2}$ 符合“特定规律”的是（）

A、 $y_{1} = x^{2} + 8$ 和 $y_{2} = - x^{2} + 2 x$ B、 $y_{1} = x^{2} + x$ 和 $y_{2} = - x + 8$ C、 $y_{1} = x^{2} + 8$ 和 $y_{2} = - x^{2} - 2 x$ D、 $y_{1} = x^{2} + x$ 和 $y_{2} = - x - 8$

查看试题解析
9. 如图，已知 $∠ A O B$ ，以点O为圆心，适当长为半径作圆弧，与角的两边分别交于C ， D两点，分别以点C ， D为圆心，大于 $\frac{1}{2} C D$ 长为半径作圆弧，两条圆弧交于 $∠ A O B$ 内一点P ，连接 $O P$ ，过点P作直线 $P E ∥ O A$ ，交OB于点E ，过点P作直线 $P F ∥ O B$ ，交 $O A$ 于点F ．若 $∠ A O B = 60 °$ ， $O P = 6 c m$ ，则四边形 $P F O E$ 的面积是（）

A、 $12 \sqrt{3} c m^{2}$ B、 $6 \sqrt{3} c m^{2}$ C、 $3 \sqrt{3} c m^{2}$ D、 $2 \sqrt{3} c m^{2}$

查看试题解析
10. 如图，已知正方形 $A B C D$ 和正方形 $B E F G$ ，且 $A 、 B 、 E$ 三点在一条直线上，连接 $C E$ ，以 $C E$ 为边构造正方形 $C P Q E$ ， $P Q$ 交 $A B$ 于点 $M$ ，连接 $C M$ ．设 $∠ A P M = α$ ， $∠ B C M = β$ ．若点 $Q 、 B 、 F$ 三点共线， $t a n α = n t a n β$ ，则 $n$ 的值为（）

A、 $\frac{2}{3}$ B、 $\frac{3}{5}$ C、 $\frac{6}{7}$ D、 $\frac{12}{13}$

查看试题解析

二、填空题（本大题共6个小题，每小题3分，共18分）

11. 计算（ $\sqrt{3} + 1$ ）（ $\sqrt{3} - 1$ ）的结果等于．

查看试题解析
12. 如图，在 $△ A B C$ 中， $A B = A C$ ．过点 $C$ 作 $∠ A C B$ 的平分线交 $A B$ 于点 $D$ ，过点 $A$ 作 $A E ∥ D C$ ，交 $B C$ 延长线于点 $E$ ．若 $∠ E = 36 °$ ，则 $∠ B =$ $°$ ．

查看试题解析
13. 已知在二次函数 $y = a x^{2} + b x + c$ 中，函数值 $y$ 与自变量 $x$ 的部分对应值如表：
$x$
$⋯$
$- 1$
0
1
2
3
$⋯$
$y$
$⋯$
8
3
0
$- 1$
0
$⋯$
则满足方程 $a x^{2} + b x + c = 3$ 的解是

查看试题解析
14. 如图，P为直径 $A B$ 上的一点，点M和N在 $⊙ O$ 上，且 $∠ A P M = ∠ N P B = 30 °$ ．若 $O P = 2 c m$ ， $A B = 16 c m$ ，则 $P N + P M =$ $c m$ ．

查看试题解析
15. 如图 1 是一款重型订书机，其结构示意图如图 2 所示.其主体部分为矩形 EFGH，由支撑杆 CD 垂直固定于底座 AB 上，且可以绕点 D 旋转.压杆 MN 与伸缩片 PG 连接，点 M 在HG 上，MN 可绕点 M 旋转，PG⊥HG ，DF＝8 cm，GF=2cm，不使用时，EF $∥$ AB，G 是 PF 中点，且点 D 在 NM 的延长线上，则 MG= cm，使用时如图3，按压 MN 使得 MN $∥$ AB，此时点 F 落在 AB 上，若 CD＝2 cm，则压杆 MN 到底座 AB 的距离为 cm

查看试题解析
16. 由四个全等的直角三角形和一个小正方形组成的大正方形 $A B C D$ 如图所示．将小正方形对角线 $E F$ 双向延长，分别交边 $A B$ ，和边 $B C$ 的延长线于点G，H．若大正方形与小正方形的面积之比为5， $G H = 2 \sqrt{10}$ ，则大正方形的边长为．

查看试题解析

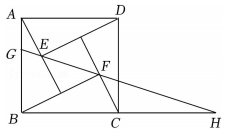
三、解答题（本大题共8个小题，共72分．解答应写出文字说明，证明过程或演算步骤）

17.

(1)、计算： $(π - 2023)^{0} + | \sqrt{3} - 2 | + \sqrt{12}$ ；

(2)、解不等式： $3 (x - 2) > 2 (2 + x)$ ．

查看试题解析
18. 小汪解答“解分式方程： $\frac{2 x + 3}{x - 2} - 2 = \frac{x - 1}{2 - x}$ ”的过程如下，请指出他解答过程中错误步骤的序号，并写出正确的解答过程．
解：去分母得： $2 x + 3 - 1 = - (x - 1)$ …①，
去括号得： $2 x + 3 - 1 = - x + 1$ …②，
移项得： $2 x + x = 1 + 1 - 3$ …③，
合并同类项得： $3 x = - 1$ …④，
系数化为1得： $x =$ $- \frac{1}{3}$ …⑤，
∴ $x =$ $- \frac{1}{3}$ 是原分式方程的解．

查看试题解析
19. 某校初三年级开展了系列交通安全知识竞赛，从中随机抽取30名学生两次知识竞赛的成绩（百分制），并对数据（成绩）进行收集、整理、描述和分析．下面给出了部分信息．
a．这30名学生第一次竞赛成绩
b．这30名学生两次知识竞赛的获奖情况统计表

参与奖
优秀奖
卓越奖
第一次
竞赛
人数
10
10
10
平均分
82
87
95
第二次
竞赛
人数
2
12
16
平均分
84
87
93
和第二次竞赛成绩得分情况统计图：（规定：分数 $\geq 90$ ，获卓越奖； $85 \leq$ 分数 $＜ 90$ ，获优秀奖；分数 $＜ 85$ ，获参与奖）
c．第二次竞赛获卓越奖的学生成绩如下：
90，90，91，91，91，91，92，93，93，94，94，94，95，95，96，98
d ．两次竞赛成绩样本数据的平均数、中位数、众数如表：

平均数
中位数
众数
第一次竞赛
m
87.5
88
第二次竞赛
90
n
91
根据以上信息，回答下列问题：

(1)、小松同学第一次竞赛成绩是89分，第二次竞赛成绩是91分，在图中用“〇”圈出代表小松同学的点；

(2)、直接写出m ， n的值；

(3)、请判断第几次竞赛中初三年级全体学生的成绩水平较高，并说明理由．

查看试题解析

20. 某校九年级学生在数学社团课上进行了项目化学习研究，某小组研究如下：

【提出驱动性问题】如何设计纸盒？

【设计实践任务】选择“素材1”“素材2”设计了“任务1”“任务2”的实践活动．

请你尝试帮助他们解决相关问题．

素材1	利用一边长为 $40 c m$ 的正方形纸板可能设计成如图所示的无盖纸盒
素材2	如图，若在正方形硬纸板的四角各剪掉一个同样大小的小正方形，将剩余部分折成一个无盖纸盒．
【尝试解决问题】
任务1	初步探究：折一个底面积为 $484 c m^{2}$ 无盖纸盒	（1）求剪掉的小正方形的边长为多少？
任务2	折成的无盖纸盒的侧面积是否有最大值？	（2）如果有，求出这个最大值和此时剪掉的小正方形的边长；如果没有，说明理由．

查看试题解析

21. 为了保护小吉的视力，妈妈为他购买了可升降夹书阅读架（如图1），将其放置在水平桌面上的侧面示意图（如图2），测得底座高 $A B$ 为 $2 c m, ∠ A B C = 150 °$ ，支架 $B C$ 为 $18 c m$ ，面板长 $D E$ 为 $24 c m, C D$ 为 $6 c m$ ．（厚度忽略不计）

(1)、求支点 $C$ 离桌面 $l$ 的高度；（计算结果保留根号）

(2)、小吉通过查阅资料，当面板 $D E$ 绕点 $C$ 转动时，面板与桌面的夹角 $α$ 满足 $30 ° \leq α \leq 70 °$ 时，能保护视力．当 $α$ 从 $30 °$ 变化到 $70 °$ 的过程中，问面板上端 $E$ 离桌面 $l$ 的高度是增加了还是减少了？增加或减少了多少？（精确到 $0.1 c m$ ，参考数据： $s i n 70 ° \approx 0.94$ ， $c o s 70 ° \approx 0.34, t a n 70 ° \approx 2.75$ ）

查看试题解析
22. 正方形 $A B C D$ 边长为3，点E是 $C D$ 上一点，连结 $B E$ 交 $A C$ 于点F ．

(1)、如图1，若 $C E = 1$ ，求 $C F$ 的值；

(2)、如图1， $\frac{C E}{E D} = m$ ，若 $S_{△ C B F} = \frac{3}{2}$ ，求m的值．

(3)、如图2，点G为 $B C$ 上一点，且满足 $∠ G A C = ∠ E B C$ ，设 $C E = x ， G B = y$ ，试探究y与x的函数关系．

查看试题解析
23. 如图1，E点为x轴正半轴上一点， $⊙ E$ 交x轴于A、B两点，交y轴于C、D两点，P点为劣弧 $\overset{⌢}{B C}$ 上一个动点，且 $A (- 1 ， 0)$ 、 $E (1 ， 0)$ ．

(1)、 $\overset{⌢}{B C}$ 的度数为 $°$ ；

(2)、如图2，连结 $P C$ ，取 $P C$ 中点G，连结 $O G$ ，则 $O G$ 的最大值为；

(3)、如图3，连接 $A C$ 、 $A P$ 、 $C P$ 、 $C B$ ．若 $C Q$ 平分 $∠ P C D$ 交 $P A$ 于Q点，求 $A Q$ 的长；

(4)、如图4，连接 $P A$ 、 $P D$ ，当P点运动时（不与B、C两点重合），求证： $\frac{P C + P D}{P A}$ 为定值，并求出这个定值．

查看试题解析
24. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + b x + 4$ 交 $y$ 轴于点 $A$ ，交 $x$ 轴于点 $B (- 6, 0)$ 和点 $C (2, 0)$ ，点 $Q$ 在第一象限的拋物线上，连接 $A B 、 A Q 、 B Q$ ， $B Q$ 与 $y$ 轴交于点 $N$ ．

(1)、求拋物线表达式；

(2)、点 $Q (1, \frac{7}{3})$ ，点 $M$ 在 $x$ 轴上，点 $E$ 在平面内，若 $△ B M E ≌ △ A O M$ ，且四边形 $A N E M$ 是平行四边形．
①求点 $E$ 的坐标；
②设射线 $A M$ 与 $B N$ 相交于点 $P$ ，交 $B E$ 于点 $H$ ，将 $△ B P H$ 绕点 $B$ 旋转一周，旋转后的三角形记为 $△ B P_{1} H_{1}$ ，求 $B P_{1} + \sqrt{2} O H_{1}$ 的最小值．

查看试题解析

		参与奖	优秀奖	卓越奖
第一次竞赛	人数	10	10	10
第一次竞赛	平均分	82	87	95
第二次竞赛	人数	2	12	16
第二次竞赛	平均分	84	87	93

	平均数	中位数	众数
第一次竞赛	m	87.5	88
第二次竞赛	90	n	91

$x$	$⋯$	$- 1$	0	1	2	3	$⋯$
$y$	$⋯$	8	3	0	$- 1$	0	$⋯$