2024年吉林省中考数学模拟卷(二)
试卷更新日期:2024-04-02 类型:中考模拟
一、单选题
-
1. 常言道:失之毫厘,谬以千里.当人们向太空发射火箭或者描述星际位置时,需要非常准确的数据.1"的角真的很小.把整个圆等分成360份,每份这样的弧所对的圆心角的度数是1°.1°=60'=3600".若一个等腰三角形的腰长为1千米,底边长为4.848毫米,则其顶角的度数就是1".太阳到地球的平均距离大约为1.5×108千米.若以太阳到地球的平均距离为腰长,则顶角为1"的等腰三角形底边长为( )A、24.24千米 B、72.72千米 C、242.4千米 D、727.2千米2. 下列各数: , , , , , , 中,负数有( )A、个 B、个 C、个 D、个3. 如图,下列条件中,能判定AB∥EF的是( )
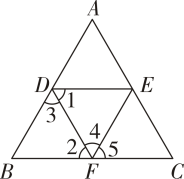
①∠B+∠BFE=180°;
②∠1=∠2;③∠3=∠4;
④∠B=∠5.A、② B、①③ C、①③④ D、②③④4. 如图,对正方体进行两次切割,得到如图⑤所示的几何体,则图⑤几何体的俯视图为( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 如图所示,在以O为原点的平面直角坐标系中,矩形OABC的两边OC,OA分别在x轴、y轴的正半轴上,反比例函数y=(x>0)的图象与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k的值为( )
5. 如图所示,在以O为原点的平面直角坐标系中,矩形OABC的两边OC,OA分别在x轴、y轴的正半轴上,反比例函数y=(x>0)的图象与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k的值为( )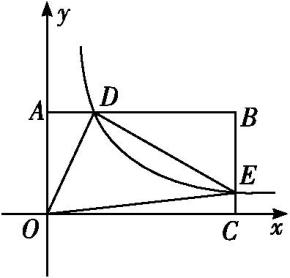 A、 B、 C、 D、126. 如图,为的直径,将沿翻折,翻折后的弧交于D.若 , , 则图中阴影部分的面积为( )
A、 B、 C、 D、126. 如图,为的直径,将沿翻折,翻折后的弧交于D.若 , , 则图中阴影部分的面积为( ) A、 B、 C、8 D、10
A、 B、 C、8 D、10二、填空题
-
7. 不等式 的最小负整数解.8. 分解因式: = .9. 已知△ABC与△A'B'C'相似,并且点A与点A'、点B与点B'、点C与点C'是对应顶点,其中∠A=80°∠B'=60°,则∠C=度.10. 如图,在矩形ABCD中,对角线AC与BD相交于点O , AE垂直且平分线段BO , 垂足为点E , , 则AB的长为 .
 11. 如图,半圆O中,C为半圆O上一点,AB为直径,∠ABC=60°,以OA为直径作半圆D , 若AB=4,则图中阴影部分的面积为 .
11. 如图,半圆O中,C为半圆O上一点,AB为直径,∠ABC=60°,以OA为直径作半圆D , 若AB=4,则图中阴影部分的面积为 .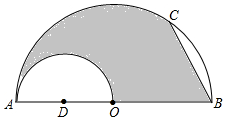 12. 我国古代数学名著《张丘建算经》中有这样一题:一只公鸡值5钱,一只母鸡值3钱,3只小鸡值1钱,现花100钱买了100只鸡.若公鸡有8只,设母鸡有x只,小鸡有y只,可列方程组为.13. 正方形和正方形中,点在上, , , 是的中点,那么的长是 .
12. 我国古代数学名著《张丘建算经》中有这样一题:一只公鸡值5钱,一只母鸡值3钱,3只小鸡值1钱,现花100钱买了100只鸡.若公鸡有8只,设母鸡有x只,小鸡有y只,可列方程组为.13. 正方形和正方形中,点在上, , , 是的中点,那么的长是 . 14. 如图1,E是正方形ABCD的边BC上一点(不与点B , C重合),连接AE , 以AE为边向右作正方形AEFG , 连接CF . 已知的面积(S)与BE的长(x)之间的函数关系如图2所示,若该抛物线顶点P的纵坐标为8,则正方形ABCD的边长为 .
14. 如图1,E是正方形ABCD的边BC上一点(不与点B , C重合),连接AE , 以AE为边向右作正方形AEFG , 连接CF . 已知的面积(S)与BE的长(x)之间的函数关系如图2所示,若该抛物线顶点P的纵坐标为8,则正方形ABCD的边长为 .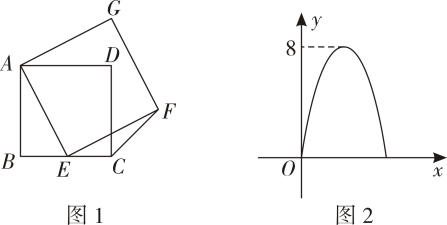
三、解答题
-
15. 先化简,再求值: , 其中 .16. 甲、乙两个盒子中装有质地、大小相同的小球,甲盒中有2个白球、1个黄球和1个蓝球;乙盒中有1个白球、2个黄球和若干个蓝球.从乙盒中任意摸取一球为蓝球的概率是从甲盒中任意摸取一球为蓝球的概率的2倍.(1)、求乙盒中蓝球的个数.(2)、从甲、乙两盒中分别任意摸取一球,利用列表或画树状图法求这两球均为蓝球的概率.17. 如图,将绕点顺时针旋转得到 , 使点的对应点落在边上.若 , 连接 , 求的度数.
 18. 某社区拟建A , B两类摊位以搞活“地摊经济”,每个A类摊位的占地面积比每个B类摊位的占地面积多2平方米,建A类摊位每平方米的费用为40元,建B类摊位每平方米的费用为30元,用60平方米建A类摊位的个数恰好是用同样面积建B类摊位个数的 .(1)、求每个A , B类摊位占地面积各为多少平方米?(2)、该社区拟建A , B两类摊位共90个,且B类摊位的数量不大于A类摊位数量的3倍,建造这90个摊位的总费用不超过10850元.则共有哪几种建造方案?(3)、在(2)的条件下,哪种方案的总费用最少?最少费用是多少?19. )某校开展了“文明城市”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题活动,每个学生限选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如图所示不完整的条形统计图和扇形统计图.
18. 某社区拟建A , B两类摊位以搞活“地摊经济”,每个A类摊位的占地面积比每个B类摊位的占地面积多2平方米,建A类摊位每平方米的费用为40元,建B类摊位每平方米的费用为30元,用60平方米建A类摊位的个数恰好是用同样面积建B类摊位个数的 .(1)、求每个A , B类摊位占地面积各为多少平方米?(2)、该社区拟建A , B两类摊位共90个,且B类摊位的数量不大于A类摊位数量的3倍,建造这90个摊位的总费用不超过10850元.则共有哪几种建造方案?(3)、在(2)的条件下,哪种方案的总费用最少?最少费用是多少?19. )某校开展了“文明城市”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题活动,每个学生限选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如图所示不完整的条形统计图和扇形统计图.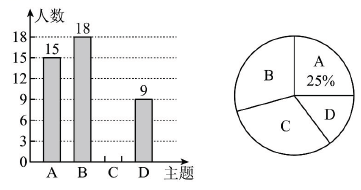
根据以上信息,解答下列问题:
(1)、补全条形统计图;(2)、在扇形统计图中,“D”主题对应扇形的圆心角为度;(3)、若该校共有3600名学生,试估计该校参与“生态环境”主题的学生人数.20. 如图,在中, , 以腰为直径画半圆 , 分别交 , 于点D , E . (1)、求证:;(2)、若 , , 求阴影部分弓形的面积.21. 如图,是由边长为1的小正方形构成的6×6网格,每个小正方形的顶点叫做格点,⊙O经过A、B、C、D四个格点,仅用无刻度的直尺在给定的网格中按要求画图(画图过程中起辅助作用的用虚线表示,画图结果用实线表示,并用黑色水笔描黑)
(1)、求证:;(2)、若 , , 求阴影部分弓形的面积.21. 如图,是由边长为1的小正方形构成的6×6网格,每个小正方形的顶点叫做格点,⊙O经过A、B、C、D四个格点,仅用无刻度的直尺在给定的网格中按要求画图(画图过程中起辅助作用的用虚线表示,画图结果用实线表示,并用黑色水笔描黑) (1)、如图1,判断圆心O(填“是”或“不是”)在格点上,并在图1中标出格点O;(2)、在图1中画出⊙O的切线CG(G为格点);(3)、在图2中画出的中点E;22. 如图,在中,是边上一点.
(1)、如图1,判断圆心O(填“是”或“不是”)在格点上,并在图1中标出格点O;(2)、在图1中画出⊙O的切线CG(G为格点);(3)、在图2中画出的中点E;22. 如图,在中,是边上一点.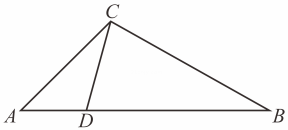 (1)、当时,
(1)、当时,①求证:;
②若 , , 求的长;
(2)、已知 , 若 , 求的长.23. 兄妹俩放学后沿图1中的马路从学校出发,到书吧看书后回家.哥哥步行先出发,途中速度保持不变:妹妹骑车,到书吧前的速度为200米/分.图2中的图象分别表示两人离学校的路程s(米)与哥哥离开学校的时间t(分)的函数关系.
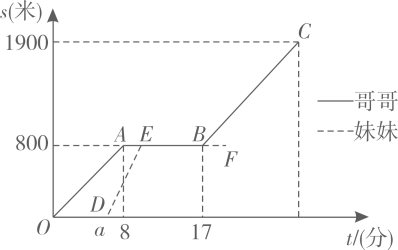 (1)、求哥哥步行的速度.(2)、已知妹妹比哥哥迟2分钟到书吧.
(1)、求哥哥步行的速度.(2)、已知妹妹比哥哥迟2分钟到书吧.
①求图中a的值;
②妹妹在书吧待了10分钟后回家,速度是哥哥的1.6倍,能否在哥哥到家前追上哥哥?若能,求追上时兄妹俩离家还有多远;若不能,说明理由.24. 如图,在平面直角坐标系中,矩形OCAB(OC>OB)的对角线长为5,周长为14.已知反比例函数y=的图象经过矩形顶点A . (1)、求反比例函数的表达式;(2)、若点(﹣a , y1)、(a+1,y2)在反比例函数的图象上,试比较y1与y2的大小;(3)、若一次函数y=kx+6的图象与反比例函数y=的图象交于E(p , ﹣3)、F(q , 4)两点,请直接写出kx+b﹣≤0成立时,对应x的取值范围.25. 根据以下素材,探索完成任务
(1)、求反比例函数的表达式;(2)、若点(﹣a , y1)、(a+1,y2)在反比例函数的图象上,试比较y1与y2的大小;(3)、若一次函数y=kx+6的图象与反比例函数y=的图象交于E(p , ﹣3)、F(q , 4)两点,请直接写出kx+b﹣≤0成立时,对应x的取值范围.25. 根据以下素材,探索完成任务如何设计拱桥上救生圈的悬挂方案?
素材1
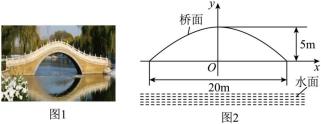
图1是一座抛物线形拱桥,以抛物线两个水平最低点连线为x轴,抛物线离地面的最高点的铅垂线为y轴建立平面直角坐标系,如图2所示.
某时测得水面宽 , 拱顶离水面最大距离为10m,抛物线拱形最高点与x轴的距离为5m.据调查,该河段水位在此基础上再涨1m达到最高.
素材2
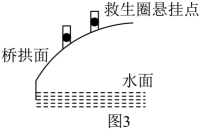
为方便救助溺水者,拟在图1的桥拱上方栏杆处悬挂救生圈,如图3,救生圈悬挂点为了方便悬挂,救生圈悬挂点距离抛物线拱面上方1m,且相邻两救生圈悬挂点的水平间距为4m.为美观,放置后救生圈关于y轴成轴对称分布.(悬挂救生圈的柱子大小忽略不计)
任务1
确定桥拱形状
根据图2,求抛物线的函数表达式.
任务2
拟定设计方案
求符合悬挂条件的救生圈个数,并求出最右侧一个救生圈悬挂点的坐标.
任务3
探究救生绳长度
当水位达到最高时,上游个落水者顺流而下到达抛物线拱形桥面的瞬间,若要确保救助者把拱桥上任何一处悬挂点的救生圈抛出都能抛到落水者身边,求救生绳至少需要多长.(救生圈大小忽略不计,结果保留整数)
问题解决
(1)、任务1 确定桥拱形状根据图2,求抛物线的函数表达式.
(2)、任务2 拟定设计方案求符合悬挂条件的救生圈个数,并求出最右侧一个救生圈悬挂点的坐标.
(3)、任务3 探究救生绳长度当水位达到最高时,上游个落水者顺流而下到达抛物线拱形桥面的瞬间,若要确保救助者把拱桥上任何一处悬挂点的救生圈抛出都能抛到落水者身边,求救生绳至少需要多长.(救生圈大小忽略不计,结果保留整数)
26. 综合与实践:在综合与实践课上,老师组织同学们以“矩形纸片的折叠”为主题开展数学活动,现有矩形纸片 , , . (1)、操作发现
(1)、操作发现操作一:如图1,将矩形纸片沿对角线折叠,使点B落在点处,将纸片展平再次折叠,使点A与点C重合,折痕为 , 然后展平得到图2,则以点A , F , C , E为顶点的四边形是什么特殊四边形?并说明理由;
(2)、实践探究操作二:如图3,在矩形纸片中,点G为的中点,将纸片沿折叠,使点B落在点处,连接 .
①判断与折痕的位置关系,并说明理由;
②求的长.
(3)、拓展应用将矩形纸片裁剪为 , , 在图3的情形下,若G为上任意一点,其他条件不变,当点A与点距离最小时,直接写出BG的长.