北师大版数学中考仿真模拟试题(三)
试卷更新日期:2024-04-02 类型:中考模拟
一、选择题(每题4分,共40分)
-
1. 下列新能源汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 将直角三角板和直尺按照如图位置摆放,若 , 则的度数是( ).
2. 将直角三角板和直尺按照如图位置摆放,若 , 则的度数是( ). A、 B、 C、 D、3. 在一个不透明的袋子中,装有个红球和若干个黑球,每个球除颜色外都相同,若从袋中任意摸出一个球是红球的概率为 , 则袋中黑球的个数为( )A、 B、 C、 D、4. 某几何体是由四个大小相同的小立方块拼成,其俯视图如图所示,图中数字表示该位置上的小立方块个数,则这个几何体的左视图是( )
A、 B、 C、 D、3. 在一个不透明的袋子中,装有个红球和若干个黑球,每个球除颜色外都相同,若从袋中任意摸出一个球是红球的概率为 , 则袋中黑球的个数为( )A、 B、 C、 D、4. 某几何体是由四个大小相同的小立方块拼成,其俯视图如图所示,图中数字表示该位置上的小立方块个数,则这个几何体的左视图是( )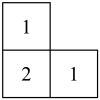 A、
A、 B、
B、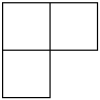 C、
C、 D、
D、 5. 估计的值应在( )A、7和8之间 B、8和9之间 C、9和10之间 D、10和11之间6. 将含角的直角三角板按如图所示放置到一组平行线中,若 , 则等于( )
5. 估计的值应在( )A、7和8之间 B、8和9之间 C、9和10之间 D、10和11之间6. 将含角的直角三角板按如图所示放置到一组平行线中,若 , 则等于( ) A、 B、 C、 D、7. 如图,直线、与双曲线分别相交于点 . 若四边形的面积为4,则的值是( )
A、 B、 C、 D、7. 如图,直线、与双曲线分别相交于点 . 若四边形的面积为4,则的值是( )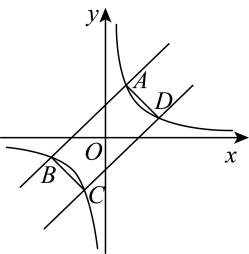 A、 B、 C、 D、18. 如图,半径为的扇形中, , 是上一点, , , 垂足分别为 , , 若 , 则图中阴影部分面积为( )
A、 B、 C、 D、18. 如图,半径为的扇形中, , 是上一点, , , 垂足分别为 , , 若 , 则图中阴影部分面积为( )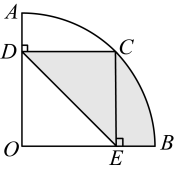 A、 B、 C、 D、9. 如图,已知正方形的边长为 , 点是对角线上的一点,于点 , 于点 , 连接 , 当::时,则( )
A、 B、 C、 D、9. 如图,已知正方形的边长为 , 点是对角线上的一点,于点 , 于点 , 连接 , 当::时,则( )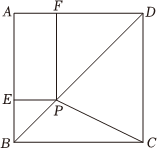 A、 B、 C、 D、10. 如图,要围一个矩形菜园 , 共中一边是墙,且的长不能超过 , 其余的三边用篱笆,且这三边的和为 . 有下列结论:
A、 B、 C、 D、10. 如图,要围一个矩形菜园 , 共中一边是墙,且的长不能超过 , 其余的三边用篱笆,且这三边的和为 . 有下列结论:①的长可以为;
②的长有两个不同的值满足菜园面积为;
③菜园面积的最大值为 .
其中,正确结论的个数是( )
 A、0 B、1 C、2 D、3
A、0 B、1 C、2 D、3二、填空题(每题4分,共24分)
-
11. 关于x的方程的解为非负数,则m的取值范围是 .12. 张师傅去年开了一家超市,今年2月份开始盈利,3月份盈利5000元,5月份盈利达到7200元,从3月到5月,每月盈利的平均增长率都相同,则每月盈利的平均增长率是 .13. 一副三角板按如图所示放置,点A在上,点F在上,若 , 则°.
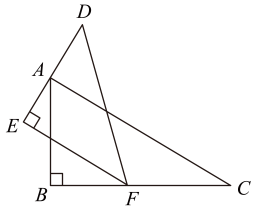 14. 广元市聚焦“1345”发展战略和“十四五”规划,牢牢牵住重点项目建设“牛鼻子”,《2023年广元市重点项目名单》共编列项目300个,其中生态环保项目10个,计划总投资约45亿元,将45亿这个数据用科学记数法表示为 .15. 如图,在Rt中, , 将绕点逆时针方向旋转 , 得到.连接 , 交AC于点 , 则的值为.
14. 广元市聚焦“1345”发展战略和“十四五”规划,牢牢牵住重点项目建设“牛鼻子”,《2023年广元市重点项目名单》共编列项目300个,其中生态环保项目10个,计划总投资约45亿元,将45亿这个数据用科学记数法表示为 .15. 如图,在Rt中, , 将绕点逆时针方向旋转 , 得到.连接 , 交AC于点 , 则的值为.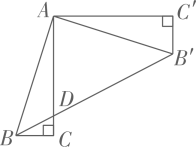 16. 我们在学习一次函数、二次函数图象的平移时知道:将一次函数的图象向上平移1个单位得到的图象;将二次函数的图象向左平移2个单位得到的图象.若将反比例函数的图象向下平移3个单位,如图所示,则得到的图象对应的函数表达式是 .
16. 我们在学习一次函数、二次函数图象的平移时知道:将一次函数的图象向上平移1个单位得到的图象;将二次函数的图象向左平移2个单位得到的图象.若将反比例函数的图象向下平移3个单位,如图所示,则得到的图象对应的函数表达式是 .
三、解答题(共9题,共86分)
-
17. 计算: .18. 先化简,再求值: , 其中满足 .19. 如图,四边形是平行四边形,连接 , 交于点 , 平分交于点 , 平分交于点 , 连接 , .
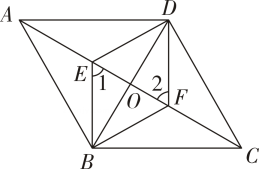 (1)、求证:;(2)、若四边形是菱形且 , , 求四边形的面积.20. 4月23日是世界读书日.为了解学生的阅读喜好,丰富学校图书资源,某校将课外书籍设置了四类:文学类、科技类、艺术类、其他类,随机抽查了部分学生,要求每名学生从中选择自己最喜欢的一类,将抽查结果绘制成如图统计图(不完整).
(1)、求证:;(2)、若四边形是菱形且 , , 求四边形的面积.20. 4月23日是世界读书日.为了解学生的阅读喜好,丰富学校图书资源,某校将课外书籍设置了四类:文学类、科技类、艺术类、其他类,随机抽查了部分学生,要求每名学生从中选择自己最喜欢的一类,将抽查结果绘制成如图统计图(不完整).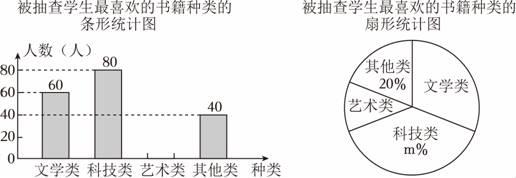
请根据图中信息解答下列问题:
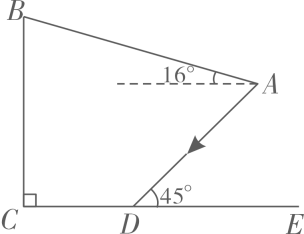
(1)、求被抽查的学生人数,并求出扇形统计图中m的值.(2)、请将条形统计图补充完整.(温馨提示:请画在答题卷相对应的图上)(3)、若该校共有1200名学生,根据抽查结果,试估计全校最喜欢“文学类”书籍的学生人数.21. 为建设美好公园社区,增强民众生活幸福感,某社区服务中心在文化活动室墙外安装遮阳篷,便于社区居民休憩.如图,在侧面示意图中,遮阳篷AB长为5米,与水平面的夹角为16°,且靠墙端离地高BC为4米,当太阳光线AD与地面CE的夹角为45°时,求阴影CD的长.(结果精确到0.1米;参考数据: , , )

 22. 如图,在Rt△ABC中,∠ACB=90°,点O在边AC上,以点O为圆心,OC为半径的半圆与斜边AB相切于点D , 交OA于点E , 连结OB .
22. 如图,在Rt△ABC中,∠ACB=90°,点O在边AC上,以点O为圆心,OC为半径的半圆与斜边AB相切于点D , 交OA于点E , 连结OB .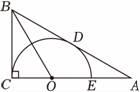 (1)、求证:BD=BC .(2)、已知OC=1,∠A=30°,求AB的长.23. 如图,一次函数的图象与反比例函数的图象分别交于点 , 点 , 与轴,轴分别交于点 , 点 , 作轴,垂足为点 , .
(1)、求证:BD=BC .(2)、已知OC=1,∠A=30°,求AB的长.23. 如图,一次函数的图象与反比例函数的图象分别交于点 , 点 , 与轴,轴分别交于点 , 点 , 作轴,垂足为点 , .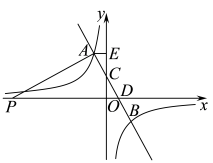 (1)、求反比例函数的表达式;(2)、在第二象限内,当时,直接写出的取值范围;(3)、点在轴负半轴上,连接 , 且 , 求点坐标.24.
(1)、求反比例函数的表达式;(2)、在第二象限内,当时,直接写出的取值范围;(3)、点在轴负半轴上,连接 , 且 , 求点坐标.24. (1)、【特例感知】
(1)、【特例感知】如图1,在正方形ABCD中,点P在边AB的延长线上,连结PD , 过点D作DM⊥PD , 交BC的延长线于点M . 求证:△DAP≌△DCM .
(2)、【变式求异】如图2,在Rt△ABC中,∠ABC=90°,点D在边AB上,过点D作DQ⊥AB , 交AC于点Q , 点P在边AB的延长线上,连结PQ , 过点Q作QM⊥PQ , 交射线BC于点M . 已知BC=8,AC=10,AD=2DB , 求的值.
(3)、【拓展应用】如图3,在Rt△ABC中,∠BAC=90°,点P在边AB的延长线上,点Q在边AC上(不与点A , C重合),连结PQ , 以Q为顶点作∠PQM=∠PBC , ∠PQM的边QM交射线BC于点M . 若AC=mAB , CQ=nAC(m , n是常数),求的值(用含m , n的代数式表示).
25. 如图,在平面直角坐标系中,直线l与x轴交于点 , 与y轴交于点 , 抛物线经过点A , B , 且对称轴是直线.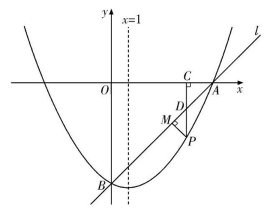 (1)、求直线l的解析式;(2)、求抛物线的解析式;(3)、点P是直线l下方抛物线上的一动点,过点P作轴,垂足为C , 交直线l于点D , 过点P作 , 垂足为M.求的最大值及此时P点的坐标.
(1)、求直线l的解析式;(2)、求抛物线的解析式;(3)、点P是直线l下方抛物线上的一动点,过点P作轴,垂足为C , 交直线l于点D , 过点P作 , 垂足为M.求的最大值及此时P点的坐标.