2023-2024学年冀教版初中数学八年级下册 22.7 多边形的内角和与外角和同步分层训练培优题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 如果正多边形的每个外角等于40°,则这个正多边形的边数是( )A、10 B、9 C、8 D、72. 当多边形的边数增加1时,它的内角和会( )A、增加90° B、增加180° C、增加270° D、增加360°3. 若一个正多边形的每一个内角的度数都是 , 则这个多边形是( )A、正九边形 B、正十边形 C、正十一边形 D、正十二边形4. 若一个多边形截去一个角后,形成的新多边形的内角和是 . 则原来多边形的边数可能是( )A、10或11 B、11 C、11或12 D、10或11或125. 如图,将边长相等的正方形、正五边形和正六边形摆放在平面上,则的度数是( )
 A、42° B、36° C、52° D、32°6. 如图,AC平分∠BAD , 过C点作CE⊥AB于E , 并且2AE=AB+AD , 则下列结论正确的是①AB=AD+2BE;②∠DAB+∠DCB=180°;③CD=CB;④S△ABC=S△ACD+S△BCE , 其中不正确的结论个数有( )
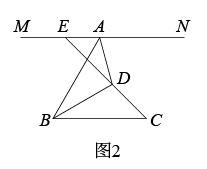
A、42° B、36° C、52° D、32°6. 如图,AC平分∠BAD , 过C点作CE⊥AB于E , 并且2AE=AB+AD , 则下列结论正确的是①AB=AD+2BE;②∠DAB+∠DCB=180°;③CD=CB;④S△ABC=S△ACD+S△BCE , 其中不正确的结论个数有( ) A、0 B、1 C、2 D、37. 已知n边形的每个内角都相等,则使得n边形的每个内角的度数都是整数的n的值有( )A、18个 B、20个 C、22个 D、无数个8. 如图,△ABC中,∠ABC、∠EAC的角平分线BP、AP交于点P,延长BA、BC,PM⊥BE,PN⊥BF,则下列结论中正确的个数( )
A、0 B、1 C、2 D、37. 已知n边形的每个内角都相等,则使得n边形的每个内角的度数都是整数的n的值有( )A、18个 B、20个 C、22个 D、无数个8. 如图,△ABC中,∠ABC、∠EAC的角平分线BP、AP交于点P,延长BA、BC,PM⊥BE,PN⊥BF,则下列结论中正确的个数( )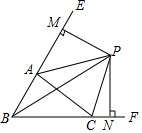
①CP平分∠ACF;②∠ABC+2∠APC=180°;③∠ACB=2∠APB;④S△PAC=S△MAP+S△NCP.
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 已知一个多边形的边数恰好是从一个顶点出发的对角线条数的1.5倍,则这个多边形的内角和为.10. 如图,在四边形ABCD中,∠A=80°,∠D=110°,∠ABC的邻补角为75°,则∠C的度数为°.
 11. 在四边形ABCD中,∠A:∠B:∠C=2:3:4,∠D=90°,则∠A=°,∠B=°,∠C=°.12. 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数为 .
11. 在四边形ABCD中,∠A:∠B:∠C=2:3:4,∠D=90°,则∠A=°,∠B=°,∠C=°.12. 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数为 . 13. 如图,在四边形中, , , , 连接 , , 则以下结论:①;②;③;④ , 其中正确的结论有.(填序号)
13. 如图,在四边形中, , , , 连接 , , 则以下结论:①;②;③;④ , 其中正确的结论有.(填序号)
三、解答题
-
14. 如图,OC平分∠AOB,P为OC上的一点,∠MPN的两边分别与OA、OB相交于点M、N.
 (1)、如图1,若∠AOB=90°,∠MPN=90°,过点P作PE⊥OA于点E,作PF⊥OB于点F,请判断PM与PN的数量关系,并说明理由;(2)、如图2,若∠AOB=120°,∠MPN=60°,求证:OP=OM+ON.15.
(1)、如图1,若∠AOB=90°,∠MPN=90°,过点P作PE⊥OA于点E,作PF⊥OB于点F,请判断PM与PN的数量关系,并说明理由;(2)、如图2,若∠AOB=120°,∠MPN=60°,求证:OP=OM+ON.15.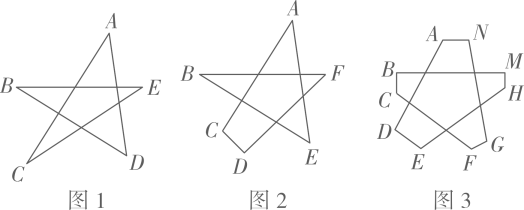 (1)、如图1,∠A+∠B+∠C+∠D+∠E=°.(2)、若将图1中星形的一个角截去,如图2,则∠A+∠B+∠C+∠D+∠E+∠F=°.(3)、若再将图2中图形的角截去,如图3,则由(2)中所得的方法或规律,猜想∠A+∠B+∠C+∠D+∠E+∠F+∠F+∠H+∠M+∠N=°.
(1)、如图1,∠A+∠B+∠C+∠D+∠E=°.(2)、若将图1中星形的一个角截去,如图2,则∠A+∠B+∠C+∠D+∠E+∠F=°.(3)、若再将图2中图形的角截去,如图3,则由(2)中所得的方法或规律,猜想∠A+∠B+∠C+∠D+∠E+∠F+∠F+∠H+∠M+∠N=°.四、综合题