2023-2024学年冀教版初中数学八年级下册 22.6 正方形同步分层训练培优题
试卷更新日期：2024-04-02 类型：同步测试
一、选择题
-
1. 菱形、矩形、正方形都具有的性质是（ ）A、两组对边分别平行且相等 B、对角线相等 C、四条边相等，四个角相等 D、对角线互相垂直2. 下列关于▱ABCD的说法，正确的是（ ）A、若AB⊥BC，则▱ABCD是菱形 B、若AC⊥BD，则▱ABCD是正方形 C、若AC=BD，则▱ABCD是矩形 D、若AB=AD，则▱ABCD是正方形3. 在四边形ABCD中，O是对角线的交点，下列条件中，能判定这个四边形为正方形的是 （ ）A、AC=BD，AB∥CD，AB=CD B、AD=BC，∠BAD=∠BCD C、AO=CO，BO=DO，AB=BC D、AO=BO=CO=DO，AC⊥BD4. 如图，在正方形 ABCD中，G是对角线BD上一点，GE⊥CD，GF⊥BC，垂足分别为 E，F.连结 AG，EF，则下列结论中，正确的是 （ ）
A、AG=BG B、AG=FG C、AG=EF D、AG=AD5. 如图所示，将三个大小相同的正方形的一个顶点重合放置，则、、三个角的数量关系为（ ）
A、 B、 C、 D、6. 如图，在正方形ABCD外取一点 ， 连接AE、BE、DE.过点作AE的垂线交DE于点.若.下列结论：①；②点到直线AE的距离是；③；④.其中正确的结论是（ ）
A、①② B、①④ C、①③④ D、①②③7. 七巧板是我国祖先的一项卓越创造，如图1，正方形ABCD可以制作一副七巧板，现将这副七巧板拼成如图2所示的“风车”造型(内部有一处空缺)，连结最外围的风车顶点 M，N，P，Q得到一个四边形MNPQ，则正方形ABCD与四边形MNPQ的面积之比为 （ ）
A、5：8 B、3 ： 5 C、8： 13 D、25：498. 如图，在△ABC中，∠ACB＝90°，以AC，BC和AB为边向上作正方形ACEF和正方形BCMI和正方形ABGF，点G落在MI上，若AC＋BC＝7，空白部分面积为16，则图中阴影部分的面积是（ ）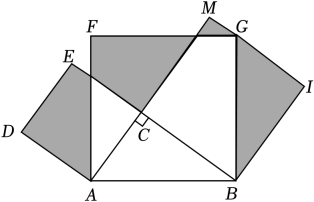
A、16 B、15 C、. D、二、填空题
-
9. 已知在平面直角坐标系中，四边形 ABCD 的四个顶点的坐标依次是A(1，1)，B(-1，1)，C(-1，-1)，D(1，-1)，则四边形 ABCD 是形.10. 如图， ▱ ABCD的对角线AC，BD 相交于点O，∠BAO=∠DAO.若添加一个条件使 ▱ ABCD为正方形，则可以添加的条件 是.
11. 如图，已知正方形ABCD的边长为2，以顶点C、D为圆心，2为半径的两弧交于点E ， 点F为AB边的中点，连接EF ， 则EF的长为 ．
12. 如图，正方形ABCD中，点E．F分别在边BC，CD上，AB=6， ， 连接BD交AF于点N，交AE于点M，若 ， 则DN为 ．
13. 如图，已知正方形的边长为4，M是对角线上的一个动点（不与B ， D重合），连接 ， 过M分别作的垂线段垂足分别为E ， F ， 则的最小值是 ．
三、解答题
-
14. 如图，已知在正方形中， ， 点为线段上一点点不与、重合 ， 连接 ， 过点作交射线于点 ， 以、为邻边作矩形 ．
(1)、求证：；(2)、连接 ， 设 ， 的面积为求关于的函数关系式并写出自变量的取值范围；(3)、当时，求的度数．15. 如图，在平行四边形ABCD中，AD=9 cm，CD= cm，∠B=45°，点M，N分别以A，C为起点，以1 cm/s的速度沿AD，CB边运动，设点M，N运动的时间为t s(0≤t≤6)． ．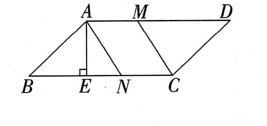
(1)、求BC边上的高AE的长度．(2)、连结AN，CM，当t为何值时，四边形AMCN为菱形？(3)、作MP⊥BC于点P，NQ⊥AD于点Q，当t为何值时，四边形MPNQ为正方形？四、综合题
-
16. 如图，在正方形ABCD中，E、F分别是边CD、BC上的两点，且 ． AE、AF分别交正方形的对角线BD于G、H两点，将△ADE绕点A顺时针旋转90°后，得到△ABQ ， 连接EF ．
(1)、求证：FA平分∠QAE ．(2)、求证： ．(3)、试探索BH、HG、GD三条线段间的数量关系，并加以说明．17.如图1，在正方形ABCD内作∠EAF=45°，AE交BC于点E，AF交CD于点F，连接EF，过点A作AH⊥EF，垂足为H．
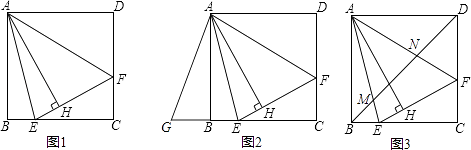(1)、如图2，将△ADF绕点A顺时针旋转90°得到△ABG．①求证：△AGE≌△AFE；
②若BE=2，DF=3，求AH的长．
(2)、如图3，连接BD交AE于点M，交AF于点N．请探究并猜想：线段BM，MN，ND之间有什么数量关系？并说明理由．