2023-2024学年冀教版初中数学八年级下册 22.6 正方形同步分层训练提升题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 下列命题中,属于假命题的是( )A、菱形的面积等于两条对角线乘积的一半 B、矩形的对角线相等 C、对角线互相垂直的平行四边形是矩形 D、对角线相等的菱形是正方形2. 如图,四边形ABCD是平行四边形,下列说法不正确的是( )
 A、当AC=BD时,四边形ABCD是矩形 B、当AB=BC时,四边形ABCD是菱形 C、当AC平分∠BAD时,四边形ABCD是菱形 D、当∠DAB= 90°时,四边形ABCD是正方形3. 下列说法正确的是( )A、四边相等的四边形是正方形 B、对角线互相垂直且相等的四边形是正方形 C、对角线相等的四边形是矩形 D、对角线互相垂直平分的四边形是菱形4. 如图,在平面直角坐标系中,点C位于第一象限,点B位于第四象限,四边形OABC 是边长为1的正方形,OC与x轴正半轴的夹角为15°,则点B的纵坐标为 ( )
A、当AC=BD时,四边形ABCD是矩形 B、当AB=BC时,四边形ABCD是菱形 C、当AC平分∠BAD时,四边形ABCD是菱形 D、当∠DAB= 90°时,四边形ABCD是正方形3. 下列说法正确的是( )A、四边相等的四边形是正方形 B、对角线互相垂直且相等的四边形是正方形 C、对角线相等的四边形是矩形 D、对角线互相垂直平分的四边形是菱形4. 如图,在平面直角坐标系中,点C位于第一象限,点B位于第四象限,四边形OABC 是边长为1的正方形,OC与x轴正半轴的夹角为15°,则点B的纵坐标为 ( ) A、-2 B、 C、 D、5. 如图,正方形ABCD 的边长为 4,点E 在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为 F,则EF 的长为 ( )
A、-2 B、 C、 D、5. 如图,正方形ABCD 的边长为 4,点E 在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为 F,则EF 的长为 ( ) A、1 B、 C、 D、6. 如图,在正方形ABCD中,E为边CD上一点,F为BC延长线上一点,CE=CF.若∠BEC= 80°,则∠EFD的度数为( )
A、1 B、 C、 D、6. 如图,在正方形ABCD中,E为边CD上一点,F为BC延长线上一点,CE=CF.若∠BEC= 80°,则∠EFD的度数为( ) A、20° B、25° C、35° D、40°7. 如图,在四边形ABCD中,AD∥BC,∠C=45°,以AB为腰作等腰直角三角形BAE,顶点E恰好落在CD边上,若AD=1,则CE的长是( )
A、20° B、25° C、35° D、40°7. 如图,在四边形ABCD中,AD∥BC,∠C=45°,以AB为腰作等腰直角三角形BAE,顶点E恰好落在CD边上,若AD=1,则CE的长是( ) A、 B、 C、2 D、18. 将两张全等的矩形纸片和另两张全等的正方形纸片按如图所示的方式不重叠地放置在矩形ABCD内,其中矩形纸片和正方形纸片的周长相等.若知道图中阴影部分的面积,则一定能求出( )
A、 B、 C、2 D、18. 将两张全等的矩形纸片和另两张全等的正方形纸片按如图所示的方式不重叠地放置在矩形ABCD内,其中矩形纸片和正方形纸片的周长相等.若知道图中阴影部分的面积,则一定能求出( ) A、正方形纸片的面积 B、四边形EFGH的面积 C、△BEF的面积 D、△AEH的面积
A、正方形纸片的面积 B、四边形EFGH的面积 C、△BEF的面积 D、△AEH的面积二、填空题
-
9. 如图,四边形ABCD是正方形,延长AB至点E,使AE=AC,连结CE,则∠BCE的度数为°.
 10. 如图,O是正方形ABCD 对角线的交点,E 是线段AO上一点.若 AB= , OE=1, 则 DE 的长为.
10. 如图,O是正方形ABCD 对角线的交点,E 是线段AO上一点.若 AB= , OE=1, 则 DE 的长为. 11. 四边形是正方形,E , F分别是和的延长线上的点,且 , 连接 , , .若 , , 则的面积为.
11. 四边形是正方形,E , F分别是和的延长线上的点,且 , 连接 , , .若 , , 则的面积为. 12. 如图,在矩形ABCD中,对角线AC,BD相交于点О,试添加一个条件 , 使得矩形ABCD为正方形.
12. 如图,在矩形ABCD中,对角线AC,BD相交于点О,试添加一个条件 , 使得矩形ABCD为正方形. 13. 如图,在四边形中, , 分别以为一边向外作正方形甲、乙、丙、丁,若用 , , , 来表示它们的面积,则(填>,<或=).
13. 如图,在四边形中, , 分别以为一边向外作正方形甲、乙、丙、丁,若用 , , , 来表示它们的面积,则(填>,<或=).
三、解答题
-
14. 如图,以边长为2的正方形的对角线的交点O 为端点,引两条相互垂直的射线,分别与正方形的边相交于A,B两点,连结AB,求线段AB 长的最小值.
 15. 如图,四边形是菱形,对角线、交于点O , 点D、B是对角线所在直线上两点,且 , 连接、、、 , .
15. 如图,四边形是菱形,对角线、交于点O , 点D、B是对角线所在直线上两点,且 , 连接、、、 , .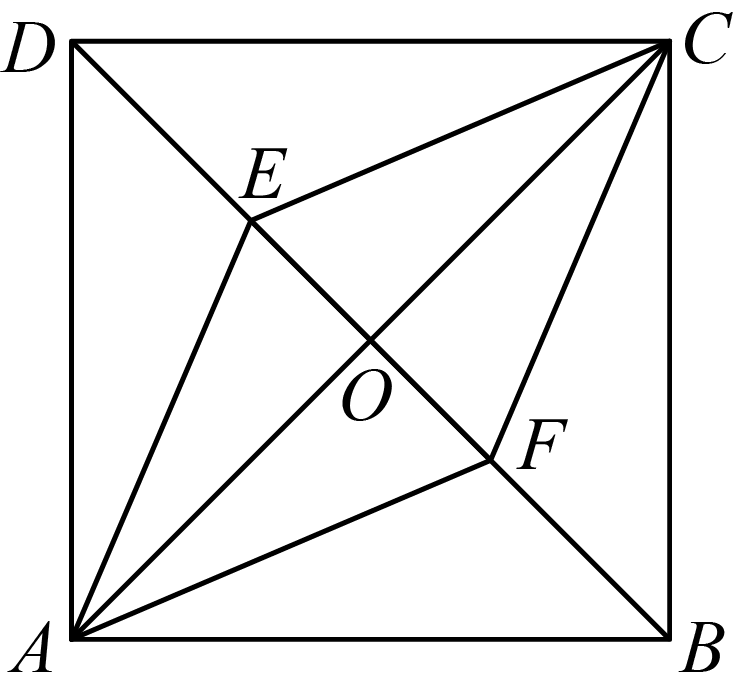 (1)、求证:四边形是正方形:(2)、若四边形的面积为72, , 求点F到线段的距离.
(1)、求证:四边形是正方形:(2)、若四边形的面积为72, , 求点F到线段的距离.四、综合题
-
16. 如图所示,将边长为a的小正方形和边长为b的大正方形放在同一水平面上().
 (1)、用a、b表示阴影部分的面积;(2)、计算当 , 时,阴影部分的面积.17. 将一副直角三角板DOE与AOC叠放在一起,如图①所示,∠O=90°,∠A=30°,∠E=45°,OD>OC.在两三角板所在平面内,将三角板DOE绕点O顺时针方向旋转α(0°<α< 90°)度到D1OE1位置,使OD1∥AC,如图②.
(1)、用a、b表示阴影部分的面积;(2)、计算当 , 时,阴影部分的面积.17. 将一副直角三角板DOE与AOC叠放在一起,如图①所示,∠O=90°,∠A=30°,∠E=45°,OD>OC.在两三角板所在平面内,将三角板DOE绕点O顺时针方向旋转α(0°<α< 90°)度到D1OE1位置,使OD1∥AC,如图②. (1)、求α的值;(2)、如图③,继续将三角板DOE绕点O顺时针方向旋转β(0° < β< 90°)度,使点E落在AC边上点E2处,点D落在点D2处,设E2D交OD1于点G, OE1交AC于点H,点G是E2D2的中点.
(1)、求α的值;(2)、如图③,继续将三角板DOE绕点O顺时针方向旋转β(0° < β< 90°)度,使点E落在AC边上点E2处,点D落在点D2处,设E2D交OD1于点G, OE1交AC于点H,点G是E2D2的中点.①直接写出β的值;
②试判断四边形OHE2G的形状,并说明理由.