2023-2024学年冀教版初中数学八年级下册 22.6 正方形同步分层训练基础题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
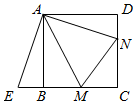
1. 下列命题是假命题的是( )A、有一组邻边相等的矩形是正方形 B、对角线互相平分的四边形是平行四边形 C、有三个角是直角的四边形是矩形 D、有一组邻边相等的四边形是菱形2. 如图,在矩形ABCD中,AD>AB,点E,F分别在边AD,BC上,EF∥AB,AE=AB,AF与BE相交于点O,连结OC.若BF=2CF,则OC与EF之间的数量关系正确的是( )
 A、 B、 C、 D、OC=EF3. 下列说法正确的是 ( )A、矩形的对角线相等且互相垂直 B、菱形的对角线相等 C、正方形的对角线相等 D、菱形的四个角都是直角4. 如图,在正方形 ABCD中,E是AC 上的一点,且 AB=AE,则∠EBC的度数为 ( )
A、 B、 C、 D、OC=EF3. 下列说法正确的是 ( )A、矩形的对角线相等且互相垂直 B、菱形的对角线相等 C、正方形的对角线相等 D、菱形的四个角都是直角4. 如图,在正方形 ABCD中,E是AC 上的一点,且 AB=AE,则∠EBC的度数为 ( ) A、37.5° B、30° C、22.5° D、12.5°5. 如图,两把完全一样的直尺叠放在起,重合的部分构成一个四边形,给出以下四个论断:这个四边形可能是正方形这个四边形一定是菱形这个四边形不可能是矩形这个四边形一定是轴对称图形,其中正确的论断是( )
A、37.5° B、30° C、22.5° D、12.5°5. 如图,两把完全一样的直尺叠放在起,重合的部分构成一个四边形,给出以下四个论断:这个四边形可能是正方形这个四边形一定是菱形这个四边形不可能是矩形这个四边形一定是轴对称图形,其中正确的论断是( )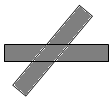 A、 B、 C、 D、6. 如图所示,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC,AF=3,△EFC的周长为12,则EC的长为( )
A、 B、 C、 D、6. 如图所示,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC,AF=3,△EFC的周长为12,则EC的长为( )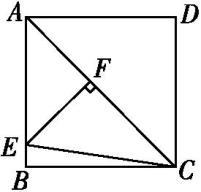 A、 B、3 C、 D、57. 四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成小正方形EFGH.已知AM为Rt△ABM较长直角边,问,当正方形ABCD的面积是小正方形EFGH面积的10倍时,两条直角边AM与BM的数量关系是( ).
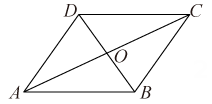
A、 B、3 C、 D、57. 四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成小正方形EFGH.已知AM为Rt△ABM较长直角边,问,当正方形ABCD的面积是小正方形EFGH面积的10倍时,两条直角边AM与BM的数量关系是( ). A、 B、BM C、BM D、BM8. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形 ,若 ,则菱形 的面积与正方形ABCD的面积之比是( )
A、 B、BM C、BM D、BM8. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形 ,若 ,则菱形 的面积与正方形ABCD的面积之比是( ) A、1 B、 C、 D、
A、1 B、 C、 D、二、填空题
-
9. 如图,在菱形ABCD中,对角线 AC,BD相交于点O,不 添 加任何 辅 助线,请 添加一个条件: , 使得四边形ABCD 是正方形.
 10. 点O是正方形ABCD的对角线AC、BD交点, , 点在BC边上,连接OF, , 则BF的长为 .11. 如图,已知正方形 的边长为3, 为 边上一点, .以点 为中心,把△ 顺时针旋转 ,得△ ,连接 ,则 的长等于
10. 点O是正方形ABCD的对角线AC、BD交点, , 点在BC边上,连接OF, , 则BF的长为 .11. 如图,已知正方形 的边长为3, 为 边上一点, .以点 为中心,把△ 顺时针旋转 ,得△ ,连接 ,则 的长等于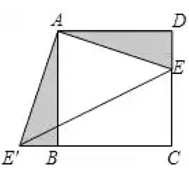 12. 如图,正方形ABCD的边长为4cm,动点E、F分别从点A、C同时出发,以相同的速度分别沿AB、CD向终点B、D移动,当点E到达点B时,运动停止,过点B作直线EF的垂线BG,垂足为点G,连接AG,则AG长的最小值为cm.
12. 如图,正方形ABCD的边长为4cm,动点E、F分别从点A、C同时出发,以相同的速度分别沿AB、CD向终点B、D移动,当点E到达点B时,运动停止,过点B作直线EF的垂线BG,垂足为点G,连接AG,则AG长的最小值为cm. 13. 如图,三个边长均为2的正方形重叠在一起,O₁,O₂是其中两个正方形的中心,则阴影部分的面积是.
13. 如图,三个边长均为2的正方形重叠在一起,O₁,O₂是其中两个正方形的中心,则阴影部分的面积是.
三、解答题
-
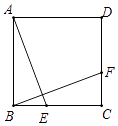
14. 如图,在正方形ABCD中,点E,F分别在BC,CD上,且BE=CF,求证:△ABE≌△BCF.
 15. 已知:如图,CE、CF分别是△ABC的内外角平分线,过点A作CE、CF的垂线,垂足分别为E、F.
15. 已知:如图,CE、CF分别是△ABC的内外角平分线,过点A作CE、CF的垂线,垂足分别为E、F. (1)、求证:四边形AECF是矩形;(2)、当△ABC满足什么条件时,四边形AECF是正方形?
(1)、求证:四边形AECF是矩形;(2)、当△ABC满足什么条件时,四边形AECF是正方形?四、综合题