冀教版初中数学八年级下册 22.5 菱形同步分层训练培优题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 如图,在菱形ABCD中,对角线AC,BD相交于点O,E为CD的中点.若OE=3,则菱形ABCD的周长为( )
 A、6 B、12 C、24 D、482. 如图,在菱形ABCD中,对角线AC与BD 相交于点O.若 AB=cm,AC=4cm,则BD的长为( )
A、6 B、12 C、24 D、482. 如图,在菱形ABCD中,对角线AC与BD 相交于点O.若 AB=cm,AC=4cm,则BD的长为( )
 A、2cm B、3cm C、4cm D、8cm3. 下列性质中,矩形具有而菱形不一定具有的是( ).A、内角和为360° B、对角线互相平分 C、对角线相等 D、对角线互相垂直4. 已知菱形的两条对角线长分别为和8cm和10cm,则菱形的面积为( )A、 B、40 C、 D、5. 在平面直角坐标系中,已知A , B , C , D四点的坐标依次为 , , , , 若一次函数()图象将四边形的面积分成1∶3两部分,则m的值为( )A、-4 B、 , -4 C、 D、 , -56. 如图,在平面直角坐标系中,菱形ABCD的顶点A , B , C在坐标轴上,若点B的坐标为 , , 则点D的坐标为( )
A、2cm B、3cm C、4cm D、8cm3. 下列性质中,矩形具有而菱形不一定具有的是( ).A、内角和为360° B、对角线互相平分 C、对角线相等 D、对角线互相垂直4. 已知菱形的两条对角线长分别为和8cm和10cm,则菱形的面积为( )A、 B、40 C、 D、5. 在平面直角坐标系中,已知A , B , C , D四点的坐标依次为 , , , , 若一次函数()图象将四边形的面积分成1∶3两部分,则m的值为( )A、-4 B、 , -4 C、 D、 , -56. 如图,在平面直角坐标系中,菱形ABCD的顶点A , B , C在坐标轴上,若点B的坐标为 , , 则点D的坐标为( ) A、 B、 C、 D、7. 如图,菱形的边长为4, , 过点B作交于点E,连接 , F为的中点,H为的中点,连接和 , 交于点G,则的长为( )
A、 B、 C、 D、7. 如图,菱形的边长为4, , 过点B作交于点E,连接 , F为的中点,H为的中点,连接和 , 交于点G,则的长为( ) A、3 B、 C、 D、8. 如图,四边形是菱形, , , 于 , 则等于( )
A、3 B、 C、 D、8. 如图,四边形是菱形, , , 于 , 则等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 已知菱形ABCD的面积为20cm²,对角线AC的长为8cm,则对角线BD的长为cm.10. 如图,在菱形ABCD中,∠D=135°,BE⊥CD于点E,交 AC 于点F,FG⊥BC 于点G.若△BFG 的周长为5,则菱形的边长为.
 11. 如图,菱形 ABCD的对角线AC,BD相交于点O,点 E 在OB 上,连结 AE,F 为CD 的中点,连结OF,若AE=BE,OE=3,OA=4,则线段OF的长为.
11. 如图,菱形 ABCD的对角线AC,BD相交于点O,点 E 在OB 上,连结 AE,F 为CD 的中点,连结OF,若AE=BE,OE=3,OA=4,则线段OF的长为.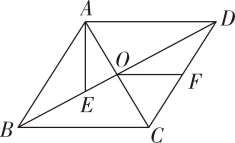 12. 如图,菱形的对角线长度为6,边长 , M为菱形外一个动点,满足 , N为中点,连接 . 则当M运动的过程中,长度的最大值为.
12. 如图,菱形的对角线长度为6,边长 , M为菱形外一个动点,满足 , N为中点,连接 . 则当M运动的过程中,长度的最大值为.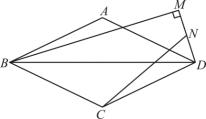 13. 已知直线的解析式为 , 菱形 , , , …按图所示的方式放置,顶点 , , , , …均在直线上,顶点 , , , …均在轴上,则点的坐标是 .
13. 已知直线的解析式为 , 菱形 , , , …按图所示的方式放置,顶点 , , , , …均在直线上,顶点 , , , …均在轴上,则点的坐标是 .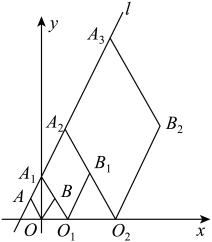
三、解答题
-
14. 如图,已知矩形 , P是AB上一动点,M、N、E分别是的中点.
 (1)、求证:四边形是平行四边形;(2)、当为何值时,四边形是菱形?并给出证明.15. 在矩形中, , , , 是对角线上的两个动点,分别从 , 同时出发相向而行,速度均为 , 运动时间为秒,当其中一个动点到达后就停止运动.
(1)、求证:四边形是平行四边形;(2)、当为何值时,四边形是菱形?并给出证明.15. 在矩形中, , , , 是对角线上的两个动点,分别从 , 同时出发相向而行,速度均为 , 运动时间为秒,当其中一个动点到达后就停止运动. (1)、若 , 分别是 , 中点,求证:四边形始终是平行四边形.(2)、在(1)条件下,当为何值时,四边形为矩形.(3)、若 , 分别是折线 , 上的动点,与 , 相同的速度同时出发,当为何值时,四边形为菱形.
(1)、若 , 分别是 , 中点,求证:四边形始终是平行四边形.(2)、在(1)条件下,当为何值时,四边形为矩形.(3)、若 , 分别是折线 , 上的动点,与 , 相同的速度同时出发,当为何值时,四边形为菱形.四、综合题
-
16. 如图,已知平面直角坐标系中,、 , 现将线段绕点顺时针旋转得到点 , 连接
 (1)、求出直线的解析式;(2)、若动点从点出发,沿线段以每分钟个单位的速度运动,过作交轴于 , 连接设运动时间为分钟,当四边形为平行四边形时,求的值.(3)、为直线上一点,在坐标平面内是否存在一点使得以、 、、为顶点的四边形为菱形?若存在,求出此时的坐标;若不存在请说明理由.17. 如图,在Rt△ABC中,∠B=90°,AC=60cm , ∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D , E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F , 连接DE , EF .
(1)、求出直线的解析式;(2)、若动点从点出发,沿线段以每分钟个单位的速度运动,过作交轴于 , 连接设运动时间为分钟,当四边形为平行四边形时,求的值.(3)、为直线上一点,在坐标平面内是否存在一点使得以、 、、为顶点的四边形为菱形?若存在,求出此时的坐标;若不存在请说明理由.17. 如图,在Rt△ABC中,∠B=90°,AC=60cm , ∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D , E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F , 连接DE , EF . (1)、填空:AE=cm,DF=cm;(用含t的代数式表示)(2)、四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;(3)、当t为何值时,△DEF为直角三角形?请说明理由.
(1)、填空:AE=cm,DF=cm;(用含t的代数式表示)(2)、四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;(3)、当t为何值时,△DEF为直角三角形?请说明理由.