2023-2024学年冀教版初中数学八年级下册 22.4 矩形同步分层训练培优题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，在矩形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点 $O$ ， $A E ⊥ B D$ 于点 $E .$ 若 $∠ A D E = 22.5 °$ ， $B D = 4$ ，则 $A E$ 的长为（）

A、 $1$ B、 $\sqrt{2}$ C、 $2 \sqrt{2}$ D、 $4$

查看试题解析
2. 下列说法中，错误的是（）

A、有一个角是直角的四边形是矩形 B、四个角都相等的四边形是矩形 C、对角线相等的平行四边形是矩形 D、对角线互相平分且相等的四边形是矩形

查看试题解析
3. 如图所示，在矩形ABCD中，AB>AD，AC与BD相交于点О，下列说法正确的是（）

A、点О为矩形ABCD的对称中心 B、点О为线段AB的对称中心 C、直线BD为矩形ABCD的对称轴 D、直线AC为线段BD的对称轴

查看试题解析
4. 如图，矩形 $A B C D$ 的两对角线相交于点 $O$ ， $∠ A O B = 60 °$ ， $B C = 3$ ，则矩形 $A B C D$ 的面积为（）

A、 $3 \sqrt{3}$ B、 $\frac{3 \sqrt{3}}{2}$ C、 $\frac{9}{2}$ D、 $\frac{9}{4}$

查看试题解析
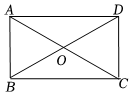5. 如图，E，F分别是矩形ABCD边AD，BC上的点，且△ABG，△DCH的面积分别为15和20，则图中阴影部分的面积为（）

A、15 B、20 C、35 D、40

查看试题解析
6. 如图，在 ▱ ABCD中，有下列条件：①AC=BD.②∠1+∠3=90°.③OB= $\frac{1}{2}$ AC.④∠1=∠2.其中能判定 ▱ ABCD是矩形的有（）

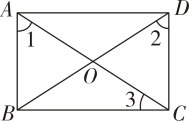A、① B、①②③ C、②③④ D、①②③④

查看试题解析
7. 如图所示，矩形ABOC的顶点O（0，0），A（－2 $\sqrt{3}$ ， 2），对角线交点为P，若矩形绕点O逆时针旋转，每次旋转90°，则第74次旋转后点P的落点坐标为（）

A、(1， $\sqrt{3}$ ) B、（2，0） C、(1，- $\sqrt{3}$ ) D、( $\sqrt{3}$ ， -1)

查看试题解析
8. 如图，正方形 $A B C D$ 边长为20，点P为正方形对角线 $B D$ 上任一点，过点P作 $P E ⊥ B C$ 于点E，作 $P F ⊥ C D$ 于点F，连接 $E F ， A P$ ．给出以下4个结论：① $A P = E F$ ；② $S_{△ A B P} = S_{四边形 B P F E}$ ；③ $A P + E F$ 的最小值是 $5 \sqrt{3}$ ；④若 $∠ B A P = 60 °$ 时，则 $E F$ 的长度为 $20 \sqrt{3} - 20$ ．其中正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 如图，在矩形ABCD中，AB=4，AD=6.在边AD上取一点E，使BE=BC，过点C作CF⊥BE，垂足为F，则BF的长为.

查看试题解析
10. 如图矩形ABCD在平面直角坐标系中，若顶点A、B、D在坐标轴上，AB＝6，∠ABD＝60°，则点D的坐标．

查看试题解析
11. 如图 $1$ 是七巧板图案，现将它剪拼成一个“台灯”造型 $($ 如图 $2)$ ，过该造型的上下左侧五点作矩形 $A B C D$ ，使得 $\frac{A B}{B C} = \frac{3}{5}$ ，点 $N$ 为 $P Q$ 的中点，并且在矩形内右上角部分留出正方形 $E F G H$ 作为印章区域 $(E H / / A D ， H G / / C D)$ ，形成一幅装饰画，则矩形 $A B C D$ 的周长为 $c m .$ 若点 $M$ ， $N$ ， $E$ 在同一直线上，且点 $H$ 到 $A D$ 的距离与到 $C D$ 的距离相等，则印章区域的边长为 $c m$ ．

查看试题解析
12. 如图，在矩形 $A B C D$ 中， $A B = 4$ ， $A D = 6$ ，点 $E$ 为边 $B C$ 上的动点，连接 $A E$ ，过点 $E$ 作 $E F ⊥ A E$ ，且 $E F = A E$ ，连接 $C F$ ，则线段 $C F$ 长度的最小值为．

查看试题解析
13. 如图，已知长方形 $A B C D$ 中， $A B = 8 c m$ ， $A D = 12 c m$ ，点 $E$ 在 $A B$ 边上， $B E = 3 c m$ ，点 $F$ 在线段 $B C$ 上以 $3 c m / s$ 的速度由 $B$ 点向 $C$ 点运动，到达点 $C$ 后马上折返，向点 $B$ 运动，点 $G$ 在线段 $C D$ 上以 $v c m / s$ 的速度由C点向D点运动．点F、G同时出发，当一个点到达终点停止运动时，另一个点也随之停止运动，设运动的时间为t秒．若以E，B，F为顶点的三角形和以F，C，G为顶点的三角形全等，则t=秒．

查看试题解析

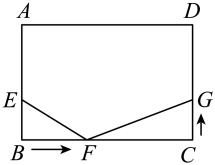
三、解答题

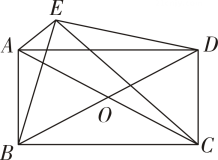
14. 如图，四边形 ABCD的对角线AC，BD相交于点O，且O是AC，BD的中点，点 E在四边形ABCD 外，连结 AE，BE，CE，DE，∠AEC =∠BED=90°，求证：四边形 ABCD 是矩形.

查看试题解析
15. 在平面直角坐标系中，四边形AOBC是矩形，点O（0，0），点A（6，0），点B（0，8）．以点A为中心，顺时针旋转矩形AOBC ，得到矩形ADEF ，点O ， B ， C的对应点分别为D ， E ， F ，记旋转角为α（0°＜α＜90°）．

(1)、如图①，当α＝30°时，求点D的坐标；

(2)、如图②，当点E落在AC的延长线上时，求点D的坐标；

(3)、当点D落在线段OC上时，求点E的坐标（直接写出结果即可）．

查看试题解析

四、综合题

16. 如图，四边形ABCD中，对角线AC、BD相交于点O，AO＝OC，BO＝OD，且∠AOB＝2∠OAD.

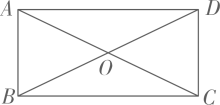(1)、求证：四边形ABCD是矩形；

(2)、若∠AOB∶∠ODC＝4∶3，求∠ADO的度数.

查看试题解析
17.

(1)、【阅读理解】如图 $①$ ，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $C D$ 是斜边 $A B$ 上的中线 $.$ 试判断 $C D$ 与 $A B$ 的数量关系 $.$ 解决此问题可以用如下方法：延长 $C D$ 至点 $E$ ，使 $D E = C D$ ，连接 $A E$ ， $B E .$ 易证四边形 $A C B E$ 是矩形，得到 $A B = E C$ ，即可作出判断 $.$ 则 $C D$ 与 $A B$ 的数量关系为；

(2)、【问题探究】如图 $②$ ，直角三角形纸片 $A B C$ 中， $∠ A C B = 90 °$ ，点 $D$ 是 $A B$ 边的中点，连接 $C D$ ，将 $△ A C D$ 沿 $C D$ 折叠，点 $A$ 落在点 $E$ 处，此时恰好有 $C E ⊥ A B .$ 若 $B C = 2$ ，求 $C E$ 的长度；

(3)、【拓展延伸】如图 $③$ ，在等腰直角三角形 $A B C$ 中， $A C = B C = 4$ ， $∠ C = 90 °$ ， $D$ 是边 $A B$ 的中点， $E$ ， $F$ 分别是边 $A C$ ， $B C$ 上的动点，且 $D E ⊥ D F$ ，当点 $E$ 从点 $A$ 运动到点 $C$ 时， $E F$ 的中点 $M$ 所经过的路径长是多少？

查看试题解析