2023-2024学年冀教版初中数学八年级下册 22.4 矩形同步分层训练基础题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

1. 关于矩形的性质、下面说法错误的是（）

A、矩形的四个角都是直角 B、矩形的两组对边分别相等 C、矩形的两组对边分别平行 D、矩形的对角线互相垂直平分且相等

查看试题解析
2. 如图，在矩形ABCD中，AO=5，CD=6，则AD的长为（）

A、5 B、6 C、7 D、8

查看试题解析
3. 已知矩形 $A B C D$ 的对角线 $A C = 4 c m$ ，则 $B D =$ （）

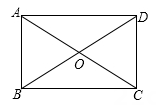A、 $1 c m$ B、 $2 c m$ C、 $3 c m$ D、 $4 c m$

查看试题解析
4. 如图，在矩形ABCD中，对角线AC ， BD相交于点O ．下列结论不一定成立的是（）

A、 $A B ⊥ B C$ B、 $A C ⊥ B D$ C、 $A C = B D$ D、 $O A = O C$

查看试题解析
5. 如图，在矩形 ABCD 中， $A B = 2$ ，对角线AC与BD相交于点 $O$ ， A E 垂直平分OB于点 E，则 BC的长为（）

A、 $2 \sqrt{5}$ B、 $2 \sqrt{3}$ C、4 D、2

查看试题解析
6. 先将一张边长为a的正方形纸片按如图1所示的方式放置于长方形 ABCD内，再将长为 b(b $\frac{1}{2}$ b 的长方形纸片按如图2，3所示的两种方式放置，长方形 ABCD未被覆盖的部分用阴影表示，设图2 中阴影部分的面积为 S₁ ，图3中阴影部分的面积为 S₂ ，且S₂-S₁=2b，则AD-AB的值为（）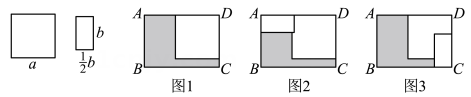

A、1 B、2 C、4 D、5

查看试题解析
7. 如图，在 Rt△ABC中，∠ACB=90°，AC=3，BC=4，M 是边 AB 上一点(不与点 A，B 重合)，过点 M 作ME⊥AC 于点E，MF⊥BC 于点 F.若 P 是EF 的中点，则CP的最小值为（）

A、1.2 B、1.5 C、2.4 D、2.5

查看试题解析
8. 如图，在矩形ABCD中，∠BAC＝60°，以点A为圆心，任意长为半径作圆弧分别交AB、AC于点M、N，再分别以点M、N为圆心，大于 $\frac{1}{2}$ MN的长为半径作弧，两弧交于点P，作射线AP交BC于点E，若BE＝1，则△AEC的面积为（）

A、1 B、2 C、 $\sqrt{3}$ D、 $2 \sqrt{3}$

查看试题解析

二、填空题

9. 如图，在矩形 $A B C D$ 中，点 $M$ ， $N$ 分别为 $B C$ ， $C D$ 的中点，若 $M N = 5$ ，则 $A C$ 的长为．

查看试题解析
10. 矩形ABCD的对角线AC、BD交于点O，∠AOD＝120°，AC＝6，则△ABO的周长为．

查看试题解析
11. 如图，点E ， F ， G ， H分别是四边形 $A B C D$ 的边 $A B$ ， $B C$ ， $C D$ ， $A D$ 的中点，连接四边形 $A B C D$ 各边中点，当四边形 $A B C D$ 满足条件，四边形 $E F G H$ 是矩形．

查看试题解析
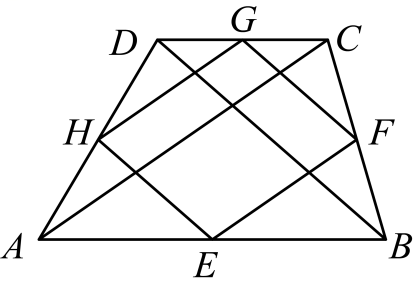12. 如图，在矩形ABCD中，AB=5，AD=12，点P 在对角线 BD上，且 BP=BA，连结 AP 并延长，交 DC的延长线于点Q，连结 BQ，则 BQ 的长为.

查看试题解析
13. 如图，已知在 Rt△ABC中，∠ABC=90°，小明按如下步骤作图：①以点 A 为圆心，BC长为半径作弧，以点 C为圆心，AB长为半径作弧，两弧相交于点 D；②连结 DA，DC，则四边形ABCD为形，判定的依据是.

查看试题解析

三、解答题

14.
如图，在▱ABCD中，AC，BD相交于点O，E，F分别是OA，OC的中点.

(1)、求证：BE=DF.

(2)、设 $\frac{A C}{B D} = k ，$ 当k为何值时，四边形DEBF是矩形?请说明理由.

查看试题解析
15. 如图，在▱ABCD中，AC，BD相交于点O，且AO=BO，∠ADB的平分线交AB于点E.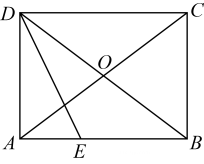

(1)、求证：▱ABCD是矩形.

(2)、若AB=8，OC=5，求AE的长.

查看试题解析

四、综合题

16. 如图，在平行四边形ABCD中，E、F为BC上两点，且BE=CF，AF=DE，求证：

(1)、△ABF≌△DCE；

(2)、四边形ABCD是矩形.

查看试题解析
17. 如图， $A D$ 和 $B C$ 相交于点 $O$ ， $∠ A B O = ∠ D C O = 90 °$ ， $O B = O C$ ．点 $E$ 、 $F$ 分别是 $A O$ 、 $D O$ 的中点．

(1)、求证： $O E = O F$ ；

(2)、当 $∠ A = 30 °$ 时，求证：四边形 $B E C F$ 是矩形．

查看试题解析